失败是成功之母,机器学习是你爹。
————奥图洛夫斯基·张小鸡
每一个认真生活的人,都应该认真学一下机器学习。骄傲者从中获得谦卑,浮躁者从中获得平静,就犹如体验过波涛风浪或生死洗礼一样。从此,便真真地知道了:自己是个弱鸡。
哔哔完了,进入正题,在此之前,希望你已经对基础的神经网络有一个了解,而反向传播算法,其实是一个寻求最优解的过程。包括我在内的很多人,一开始都认为其中的原理很难,但其实不是,反向传播算法之所以被广泛应用,除了有效性外,私以为还得益于它的容易理解。看过《土拨鼠之日》的人,一定希望拥有和男主一样的奇特经历。因为它的奇妙之处,是可以一次次地返回去实验,如果失败了,则得到反馈,再优化。相应的,反向传播算法也是如此,一次次的返回去重来,得到最优解。
下面咱们从从最简单三层神经网络开始,即输入层,隐含层和输出层。输入层包含两个神经元i1, i2,隐含层包含两个神经元h1, h2,输出层同样是两个神经元o1, o2,输入层和隐含层的偏置项分别为b1, b2,激活函数默认为sigmod函数。
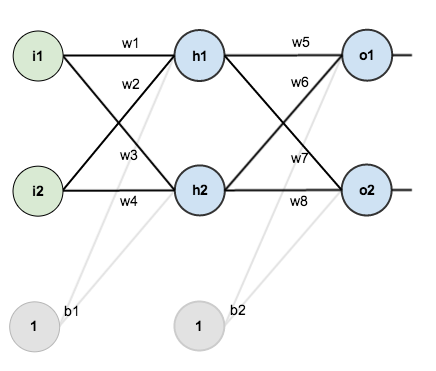
现在我们对它们附上初始值,如下图所示:
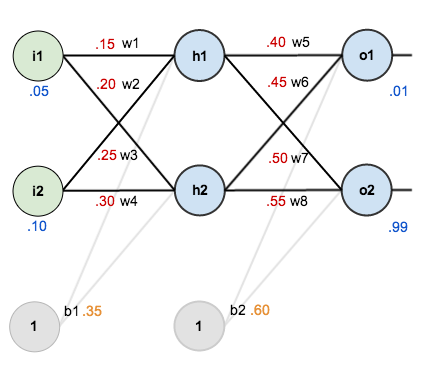
其中:
输入数据 i1=0.05,i2=0.10;
输出数据 o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.55
还记得我们的最终目标吧?给出初始值i1,i2,求出使得离目标输出最接近的系数值,即(wi, bi)
一步步的推导过程我再次不赘述,可以参考下原文或 胡晓曼大佬的文章,传送门戳蓝色字体,
我说一下具体的代码实现部分的一些细节。Matt Mazur大佬的代码清晰易读,而且分类特别赞,我们回顾一下上面的结构,发现整个神经网络系统就分为两个部分:神经元和连接神经元的线(即权重和偏置项),分工也很清晰明了。神经元负责的有:
向前传播:加权和,激活函数,输出函数,误差
反向传播:误差偏导,输出函数到激活函数的偏导,激活层到加权和的偏导
它们之间的连线,也就是网络层,负责对神经元的操控,它只需要负责向前传播和得到输出的结果。有了如上的结构,便可以来搭建整个网络了,黑喂狗~~
首先编写神经元:
class Neuron():
def __init__(self, bias):
self.bias = bias
self.weights = []
def calculate_output(self, inputs):
self.inputs = inputs
self.out_put = self.activate(self.calculate_total_net_input())
return self.out_put
def calculate_total_net_input(self):
total = 0
for i in range(len(self.inputs)):
total += self.weights[i] * self.inputs[i]
return total + self.bias
def activate(self, total_net_input):
return 1/(1+math.exp(-total_net_input))
def calculate_error(self, target_output):
return 0.5 * (target_output - self.out_put) ** 2
# ∂E/∂yⱼ
def calculate_pd_error_wrt_output(self, target_output):
return - (target_output - self.out_put)
# dyⱼ/dzⱼ = yⱼ * (1 - yⱼ)
def calculate_pd_active_wrt_total_net_input(self):
return self.out_put * (1 - self.out_put)
# ∂zⱼ/∂wᵢ = wᵢ
def calculate_pd_total_net_input_wrt_weight(self, index):
return self.inputs[index]
# δ = ∂E/∂zⱼ = ∂E/∂yⱼ * dyⱼ/dzⱼ
def calculate_pd_error_wrt_total_net_input(self, target_output):
return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_active_wrt_total_net_input()
接下来我们编写网络层部分的代码:
class NeuronLayer():
def __init__(self, num_neurons, bias):
self.bias = bias
self.neurons = []
for i in range(num_neurons):
self.neurons.append(Neuron(bias))
def feed_forward(self, inputs):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.calculate_output(inputs))
return outputs
def get_outs(self):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.out_put)
return outputs
最后,我们由它们来组合我们的整个网络结构:
class NeuralNetwork():
LEARNING_RATE = 0.5
def __init__(self, num_inputs, num_hiddens, num_outputs, hidden_layer_weights=None, hidden_layer_bias=None, output_layer_weights=None, output_layer_bias=None):
self.num_inputs = num_inputs
self.hidden_layer = NeuronLayer(num_hiddens, hidden_layer_bias)
self.output_layer = NeuronLayer(num_outputs, output_layer_bias)
self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)
def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):
weight_num = 0
for h in range(len(self.output_layer.neurons)):
for i in range(self.num_inputs):
if not hidden_layer_weights:
self.hidden_layer.neurons[h].weights.append(random.random())
else:
self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
weight_num += 1
def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):
weight_num = 0
for o in range(len(self.output_layer.neurons)):
for h in range(len(self.hidden_layer.neurons)):
if not output_layer_weights:
self.output_layer.neurons[o].weights.append(random.random())
else:
self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
weight_num += 1
def feed_forward(self, inputs):
hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)
return self.output_layer.feed_forward(hidden_layer_outputs)
def train(self, train_inputs, train_outputs):
self.feed_forward(train_inputs)
pd_errors_wrt_output_neuron_total_net_input = [0]*len(self.output_layer.neurons)
for o in range(len(self.output_layer.neurons)):
pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(train_outputs[o])
pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)
for h in range(len(self.hidden_layer.neurons)):
d_error_wrt_hidden_neuron_output = 0
for o in range(len(self.output_layer.neurons)):
d_error_wrt_hidden_neuron_output += pd_errors_wrt_hidden_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]
pd_errors_wrt_hidden_neuron_total_net_input[h] += d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_active_wrt_total_net_input()
for o in range(len(self.output_layer.neurons)):
for w_ho in range(len(self.output_layer.neurons[o].weights)):
pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)
self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight
for h in range(len(self.hidden_layer.neurons)):
for w_ih in range(len(self.hidden_layer.neurons[h].weights)):
# ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ
pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[
h].calculate_pd_total_net_input_wrt_weight(w_ih)
# Δw = α * ∂Eⱼ/∂wᵢ
self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight
以上便是通过简单的网络结构,理解反向传播算法的相关细节。从我学习和理解的过程来看,其实真正花耐心去理解,是不难的,往往真正击败我们的,真正击败我们的,往往是浮躁。道长且阻,一起加油~
参考资料:
mattmazur.com/2015/03/17/… 一文弄懂神经网络中的反向传播法--BackPropagation - Charlotte77 - 博客园