【导读】转置卷积一直不太好理解,今天我们通过详细的推导示例及代码了解简单的两层CNN中转置卷积的反向传播。
编译 | 专知
参与 | Yingying, Xiaowen
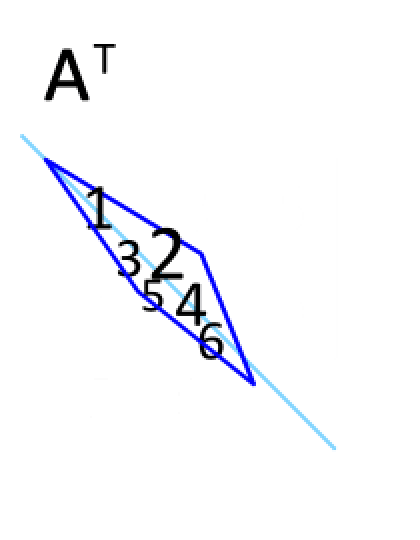
今天,我们要训练一个简单的有两个卷积层的CNN,如下所示。
灵感来源

盘子上的玉米提示了我CNN反向传播过程中的解卷积的原理。
红框是2 * 2输出图像
绿色框是3 * 3卷积核
蓝色框是4 * 4输入图像
“由于我们在对4 * 4图像执行卷积后得到2 * 2的输出图像,因此在执行反向传播时,我们需要对2 * 2输出图像执行一些操作,以获得具有4 * 4的图像。”
但玉米让我意识到目标不是恢复原始图像。 相反,应该是获得网络中每个权重的错误率。 而在多层CNN的情况下,我们需要反向传播该错误率。 让我试着通过一个具体的例子和代码来解释我的意思。
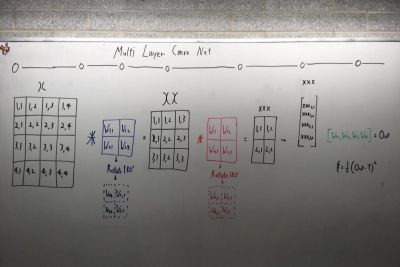
网络结构
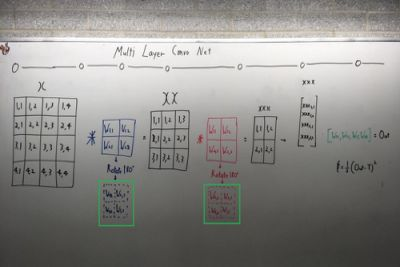
如上所示,网络结构非常简单,只有两层卷积和一层完全连接的层。 请注意,在执行卷积时,我们需要将卷积核转置(旋转)180度,请注意上图中的绿色框。
另外,请注意,为了简单我并没有绘制激活层。 但在代码中,我使用了tanh()或者archtan()作为激活函数。
前向传播

注意:作者在列上犯了一个错误,必须交换绿色箭头指向的两列。
所以如上所见,卷积操作可以写成一行。 由于我将在稍后解释的原因,请仔细记下红框变量,它们是下一层的输入。 这些信息在执行反向传播时很重要。
(上图中绿色权重的)反向传播
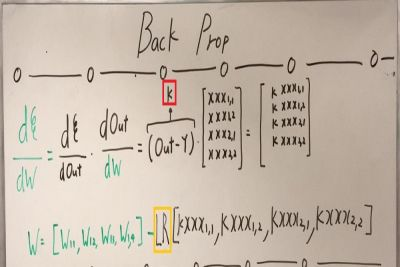
黄框代表学习率,整个反向传播就是标准的过程。我把梯度更新方程也写下来了。。 最后,请注意红框中的符号'k',我会反复使用此符号来表示(Out - Y)。
(上图中红色权重的)反向传播

红框→(Out - Y)
黄框→学习率
黑框→在卷积操作之前旋转内核180度(或转置) (记住在卷积运算中,我们旋转卷积核)。
除了紫色框,一切都非常简单直接,那紫色方框是干什么的?
紫框→旋转矩阵以适合计算每个权值量的导数。
现在的问题出现了,为什么? 我们为什么要做这个?
还记得我告诉过你们要注意每层的输入吗? 那么让我们再回去一次。

请仔细查看彩色框。
橙框→正在乘以红色W的输入W(2,2)
浅绿色框→正在乘以红色的输入W(2,1)
蓝色框→正在乘以红色W的输入W(1,2)
粉红色框→正在乘以红色的输入W()1,1)
这很简单,但是这与转置卷积核有什么关系?因为(请看黑色框方程)Out可以写成一行,红框中权值的梯度如下:

深绿色框中的数字->绿色的权值。
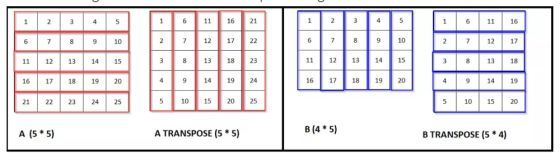
正如所看到的那样,当对每个红色权重计算导数时,我们可以看到XX坐标因输入而异。 我们需要将这些坐标与每个权重进行匹配,这就是我们将矩阵旋转180度的原因。
-
蓝色权重反向传播第1部分

篮框→计算(K *绿色重量)和(填充红色权重)之间的卷积
橙框→再次旋转矩阵得到每个权重的梯度
黑框→在卷积操作之前旋转卷积核
现在,问题出现了,为什么Padding(紫框)? 为什么我们需要填充红色权值?
这问题我们稍后解释。
-
蓝色权重反向传播第2部分

蓝框→第1部分中计算的矩阵
黑框→在卷积操作之前转置卷积核
橙色,浅绿色,蓝色,粉红色框→计算每个蓝色权值的梯度

以上是对旋转的卷积核进行更仔细的观察,同时执行卷积操作。 但现在让我们再看看输入。

再一次,因为Out可以写成一行,所以蓝色权重的梯度如下所示:

绿框→绿色权值
橙框→蓝色权值W(2,2)的梯度
粉框→蓝色权值W(1,1)的梯度
所以,我们再次旋转(或转置)矩阵以匹配每个权重的梯度。
另外,现在我们填补红色权重的原因很明显,就是为每个权重获计算梯度,我会再次向你展示我的意思是填充红色权重(请看紫色星号部分)。

激活函数
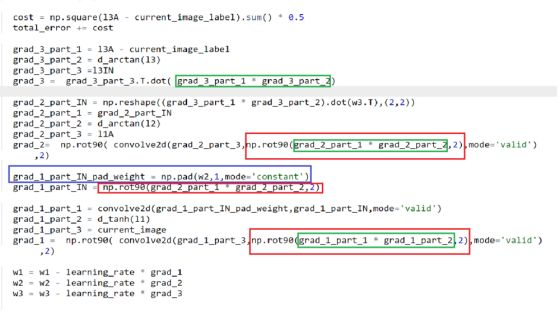
绿框→激活函数的导数,因为它们具有相同的维数,我们可以进行元素相乘
红框→旋转卷积核以匹配梯度
篮框→用零填充红色权重(命名为W2)
代码
import numpy as np,sys# Func: Only for 2D convolution from scipy.signal import convolve2dfrom sklearn.utils import shuffle# Func: For Back propagation on Max Poolingfrom scipy.ndimage.filters import maximum_filterimport skimage.measurenp.random.seed(12314)def ReLU(x): mask = (x >0) * 1.0 return mask * xdef d_ReLU(x): mask = (x >0) * 1.0 return mask def tanh(x): return np.tanh(x)def d_tanh(x): return 1 - np.tanh(x) ** 2def arctan(x): return np.arctan(x)def d_arctan(x): return 1 / ( 1 + x ** 2)def log(x): return 1 / (1 + np.exp(-1 * x))def d_log(x): return log(x) * ( 1 - log(x))# 1. Prepare Datanum_epoch = 1000learning_rate = 0.1total_error = 0x1 = np.array([ [0,0,0,-1], [-1,0,-1,0], [-1,0,-1,-1], [1,0,-1,-1] ])x2 = np.array([ [0,0,0,0], [0,0,-1,0], [0,0,0,0], [1,0,0,-1] ])x3 = np.array([ [0,0,0,-1], [0,0,-1,0], [-1,0,1,1], [1,0,-1,1] ])x4 = np.array([ [0,0,0,1], [1,0,1,0], [1,0,1,1], [1,0,1,1] ])image_label=np.array([ [-1.42889927219], [-0.785398163397], [0.0], [1.46013910562] ])image_matrix = np.array([x1,x2,x3,x4])w1 = (np.random.randn(2,2) * 4.2 )-0.1w2 = (np.random.randn(2,2)* 4.2)-0.1w3 = (np.random.randn(4,1)* 4.2)-0.1print('Prediction Before Training')predictions = np.array([])for image_index in range(len(image_matrix)): current_image = image_matrix[image_index] l1 = convolve2d(current_image,w1,mode='valid') l1A = tanh(l1) l2 = convolve2d(l1A,w2,mode='valid') l2A = arctan(l2) l3IN = np.expand_dims(l2A.ravel(),0) l3 = l3IN.dot(w3) l3A = arctan(l3) predictions = np.append(predictions,l3A)print('---Groud Truth----')print(image_label.T)print('--Prediction-----')print(predictions.T)print('--Prediction Rounded-----')print(np.round(predictions).T)print("\n")for iter in range(num_epoch): for current_image_index in range(len(image_matrix)): current_image = image_matrix[current_image_index] current_image_label = image_label[current_image_index] l1 = convolve2d(current_image,w1,mode='valid') l1A = tanh(l1) l2 = convolve2d(l1A,w2,mode='valid') l2A = arctan(l2) l3IN = np.expand_dims(l2A.ravel(),0) l3 = l3IN.dot(w3) l3A = arctan(l3) cost = np.square(l3A - current_image_label).sum() * 0.5 total_error += cost grad_3_part_1 = l3A - current_image_label grad_3_part_2 = d_arctan(l3) grad_3_part_3 =l3IN grad_3 = grad_3_part_3.T.dot( grad_3_part_1 * grad_3_part_2) grad_2_part_IN = np.reshape((grad_3_part_1 * grad_3_part_2). dot(w3.T),(2,2)) grad_2_part_1 = grad_2_part_IN grad_2_part_2 = d_arctan(l2) grad_2_part_3 = l1A grad_2= np.rot90( convolve2d(grad_2_part_3,np.rot90 (grad_2_part_1 * grad_2_part_2,2),mode='valid') ,2) grad_1_part_IN_pad_weight = np.pad(w2,1,mode='constant') grad_1_part_IN = np.rot90(grad_2_part_1 * grad_2_part_2,2) grad_1_part_1 = convolve2d(grad_1_part_IN_pad_weight,grad_1_part_IN,mode='valid') grad_1_part_2 = d_tanh(l1) grad_1_part_3 = current_image grad_1 = np.rot90( convolve2d(grad_1_part_3,np. rot90(grad_1_part_1 * grad_1_part_2,2),mode='valid') ,2) w1 = w1 - learning_rate * grad_1 w2 = w2 - learning_rate * grad_2 w3 = w3 - learning_rate * grad_3 #print('Current iter: ', iter, ' current cost: ', cost, end='\r') total_error = 0 print('\n\n')print('Prediction After Training')predictions = np.array([])for image_index in range(len(image_matrix)): current_image = image_matrix[image_index] l1 = convolve2d(current_image,w1,mode='valid') l1A = tanh(l1) l2 = convolve2d(l1A,w2,mode='valid') l2A = arctan(l2) l3IN = np.expand_dims(l2A.ravel(),0) l3 = l3IN.dot(w3) l3A = arctan(l3) predictions = np.append(predictions,l3A)print('---Groud Truth----')print(image_label.T)print('--Prediction-----')print(predictions.T)print('--Prediction Rounded-----')print(np.round(predictions).T)print("\n")完整代码链接:https://repl.it/@Jae_DukDuk/transpose-conv
原文链接:
https://towardsdatascience.com/only-numpy-understanding-back-propagation-for-transpose-convolution-in-multi-layer-cnn-with-c0a07d191981