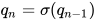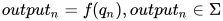作为随机选择的工具,我没有发现任何优于骰子的东西
—— Francis Galton,1890 年 《自然》
1 什么是伪随机数序列
如果从字面意思来看,『伪随机数序列』就是伪造的随机数序列。为了准确定义,在这里假设掷骰子可以得到一个真正的随机数,它的结果符合 1 ~ 6 上的均匀分布(注 1)。如果多次掷骰子,在这个过程中,可能可以看到以下序列
1, 5, 6, 5, 6, 2, 5, 4, 5, 3, 4, 5, 5, 5, 3, 4, 2, 1, 1, 3
也有可能出现这个序列
3, 6, 6, 6, 2, 3, 1, 5, 2, 2, 4, 5, 6, 3, 1, 3, 3, 5, 5, 6
甚至有可能,出现这样的序列,虽然概率很小
6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6
在不停掷骰子的过程中,在结果出来之前,永远也不会知道当前这个数是多少。我们只知道在这此掷骰子的结果中某个数可能出现的概率是多少,并且这个概率永远不会改变。这个性质也可以称为,独立同分布。或者转换一下概念,称之为不可预测性;相反的,如果只知道当前数字,也不可能确定上一次掷骰子结果。
而『伪随机数序列』是使用特定的方法,比如通过对某个数学公式的计算,生成一个数字序列,并且让这个数字序列在各方面看起来尽可能的像一个真正随机数序列。比如一个最古老的伪随机数生成算法——平方取中法(Middle-square method),它的过程如下
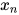 是一个 4 位十进制,比如 1234
是一个 4 位十进制,比如 1234- 计算
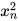 ,值为 1522756,补足 8 位,即 01522756
,值为 1522756,补足 8 位,即 01522756 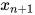 等于
等于 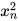 中间 4 位,即 5227
中间 4 位,即 5227
def middle_square():
global rand #伪随机数生成算法的内部状态,也是输出值
rand = rand ** 2
rand = (rand // 100) % 10000 #也可以考虑转成字符串再提取
return rand
rand = 1234 #初始状态
# 将输出进一步处理,模 6 加 1,获得[1, 6]范围内的整数
#[middle_square() % 6 + 1 for i in range(0, 20)]
将会输出序列
2, 6, 3, 1, 4, 1, 2, 5, 3, 5, 5, 1, 6, 4, 1, 5, 5, 1, 6, 4
单独看这个序列,和前面掷骰子出来结果比较,看起来还是比较像,每个数字都出现了,看似没有什么规律性。那么我们模拟了一个随机过程——一个伪随机数序列。
这里将之为伪随机数序列,只因为它和真正的随机数序列比较而言,它实际上是确定的——在平方取中法中,当第一个 rand 确定时,后续序列的所有值也就随之确定,在这个过程中没有任何随机性。
可以使用一个 4 元组 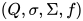 定义一个伪随机数生成算法(在习惯上,也称之为伪随机数生成器,Pseudo Random Number Generator,简称 PRNG),其中
定义一个伪随机数生成算法(在习惯上,也称之为伪随机数生成器,Pseudo Random Number Generator,简称 PRNG),其中 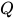 是有限状态集合,
是有限状态集合, 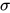 为状态转移函数,
为状态转移函数, 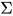 是有限输出集合,
是有限输出集合, 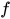 是从
是从 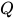 到
到 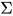 的单射。当需要一个伪随机数序列时,设定初始状态
的单射。当需要一个伪随机数序列时,设定初始状态 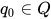 ,每一次输出都由如下两个过程组成
,每一次输出都由如下两个过程组成
对于上述的平方取中法,可以直观的得到 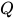 对应 [0, 9999] 中的所有整数,
对应 [0, 9999] 中的所有整数, 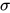 即平方取中法的计算过程,
即平方取中法的计算过程, 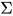 为 [0, 9999] 中的所有整数,而
为 [0, 9999] 中的所有整数,而 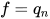 。在示例上,初始状态
。在示例上,初始状态 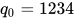
从上述定义来看,当 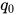 确定后,后续所有输出序列
确定后,后续所有输出序列 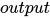 即被确定。事实上,对任何图灵机模型,或者说任何确定性有限自动机模型,其表达能力是不包括任何真正意义上的随机——当起始状态、输入和所有状态转移都被确定时,后续所有过程都将被确定。所以,在不依赖外部物理环境,而单纯使用逻辑计算,只能生成这种实质没有任何随机性的『伪随机数序列』(注
2)
即被确定。事实上,对任何图灵机模型,或者说任何确定性有限自动机模型,其表达能力是不包括任何真正意义上的随机——当起始状态、输入和所有状态转移都被确定时,后续所有过程都将被确定。所以,在不依赖外部物理环境,而单纯使用逻辑计算,只能生成这种实质没有任何随机性的『伪随机数序列』(注
2)
值得庆幸的是,我们可以定义良好的 4 元组 PRNG,使得生成序列在某些方面和真正的随机数序列有一定相似性。而这些相似性,达到一定程度时,就足够特定目的的使用。某些方面包括
A1. 生成的序列每段之间大概率(统计意义上)不一样
A2. 各项统计指标,和真正随机数序列尽可能相似,比如自相关检测
A3. 即使知道生成序列中的某一段数字,也难以确定之前的数、当前内部状态 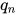 以及之后的数
以及之后的数
A4. 即使知道当前 PRNG 的当前内部状态 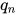 ,也难以确定出之前的状态(如
,也难以确定出之前的状态(如 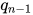 )和生成的数(如
)和生成的数(如 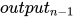 )
)
A1 - A4 是一个非常概念化的说法,更准确的定义可以参考 这篇文章。这 4 条,从上到下,表现得越良好,算法适用性越广。一般而言,对于一般的娱乐活动,或者模拟计算(比如蒙特卡洛方法),在一定程度上满足 A1、A2 条即可。对于加密安全或者高要求的赌博活动,第 A3、A4 条不可或缺,称之为 CSPRNG(Cryptographically Secure Pseudo Random Number Generator)。
在本文中,并不准备定量分析 A1 - A4 条,对于他们的具体分析过于形式化。综合 A1 - A4、和实践中的一些要求,提出以下 3 个更弱化并直观的要求
B1. 循环周期很长(由 A1 导出)。比如 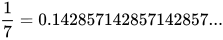 ,这个小数点后面的输出序列的周期为 6,而我们希望 PRNG 的输出序列具备很长的周期,比如
,这个小数点后面的输出序列的周期为 6,而我们希望 PRNG 的输出序列具备很长的周期,比如 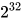 ,甚至更大
,甚至更大
B2. 输出数字序列不相关(由 A2 导出)。相关度越高体现出的随机性也越弱
B3. 高效,可以很快的给出一个伪随机数序列。计算机内之所以没有内置一个掷骰子装置,是因为太慢了^*^(注 3)
A3 和 A4 涉及的领域在本文中将被忽略,有兴趣可以参考 CSPRNG - Wikipedia
2 计数器
def counter():
global state
state += 1
return state
state = 0
#[counter() for i in range(0, 20)]
#[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
这是一个简单的计数器实现,可以设置初始值。显而易见,计数器生成序列,周期非常大,在图灵机模型中可以任意大(但有限);在现实计算机中,可以达到该计算机的表示能力上界(主要由存储能力决定)。它满足 B1,也只满足 B1。计数器生成递增序列和真正随机数序列差距太大,比如强自相关,我们很难将其作为一个 PRNG 用于实践。
3 平方取中法
在第 1 节中已经简单描述过这一方法的过程
def middle_square():
global rand #伪随机数生成算法的内部状态,也是输出值
rand = rand ** 2
rand = (rand // 100) % 10000 #也可以考虑转成字符串再提取
return rand
在上述示例中,输出和内部状态都是由 4 位整数来表达。这个算法是冯诺依曼在 19 世纪 40 年代提出了,其本身更多还是玩具性质。这个算法有几个严重缺陷,让其很难作为一个 PRNG 来使用
- 接近 20% 的初始值会让序列收敛到 0
- 其余 80% 的初始值同样会陷入其他短周期循环中
比如 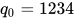 ,其第 56 次迭代即收敛到 0
,其第 56 次迭代即收敛到 0
比如 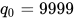 ,其第 3 次迭代即开始了周期为 4 的循环,循环序列为 1600, 5600, 3600, 9600
,其第 3 次迭代即开始了周期为 4 的循环,循环序列为 1600, 5600, 3600, 9600
对于周期很短的序列,其在 B1 的表现就已经非常差。
实际上,可以定义不同长度的 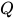 和
和 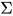 ,比如
,比如 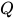 的元素是 6 位整数,而
的元素是 6 位整数,而 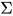 的元素是 3 位整数
的元素是 3 位整数
def middle_square():
global rand #伪随机数生成算法的内部状态,也是输出值
rand = rand ** 2
rand = (rand // 1000) % 100000 #也可以考虑转成字符串再提取
return rand % 1000
这里存在同样的问题,只是陷入周期循环更慢一些,周期相对而言可能较长而已。这其中的原因有本身 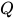 的大小限制了周期的上界,也有其实现内在固有的一些性质。比如对这个实例,一旦
的大小限制了周期的上界,也有其实现内在固有的一些性质。比如对这个实例,一旦 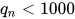 ,就会开始向 0 收敛。
,就会开始向 0 收敛。
整体来看,平方取中法生成序列只有前面一些数可用,具体有多少数字可用由 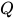 的位数决定。而当
的位数决定。而当 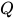 位数增大时,就需要考虑位数的限制以及计算复杂度。
位数增大时,就需要考虑位数的限制以及计算复杂度。
4 线性同余生成器,Linear congruential generator
线性同余生成器(LCG) 4 元组定义
状态转移函数 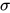 为
为
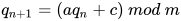
其中 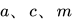 是固定值
是固定值
有限状态集合 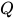 为 [0, m - 1] 中的所有整数,
为 [0, m - 1] 中的所有整数, 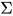 为 [0, m - 1] 中的所有整数,而
为 [0, m - 1] 中的所有整数,而 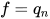 。
。
LCG 显然是非常高效的,但是它的问题在于,对不同的 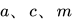 取值,特性相差很大,比如
取值,特性相差很大,比如
def lcg():
a = 31
c = 5
m = 127
global rand
rand = (a * rand + c) % m
return rand
#rand = 1
这个 LCG 函数对任意 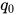 都将输出一个周期为 63 的序列,除
都将输出一个周期为 63 的序列,除 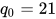 以外,此时所有输出都将是 21。很容易发现,LCG 的
以外,此时所有输出都将是 21。很容易发现,LCG 的 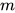 取值决定了其输出序列周期的上界。为了直观感受周期性对 PRNG 仿真的重要性,可以使用一段程序(注 4),根据不同 PRNG 生成伪随机二值图
取值决定了其输出序列周期的上界。为了直观感受周期性对 PRNG 仿真的重要性,可以使用一段程序(注 4),根据不同 PRNG 生成伪随机二值图


可以看出,前一幅图的随机性表现的更好。而后者,有极强的规律性,这主要是由其短周期导致的。
值得庆幸的是,我们可以需要选择一个很大的 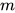 值,同时小心翼翼的选择特定
值,同时小心翼翼的选择特定 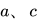 的值(注 5),以产生一个周期很长并可以达到
的值(注 5),以产生一个周期很长并可以达到 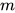 上界的输出系列。
上界的输出系列。
比如
def LCG():
a = 69069
c = 1
m = 4194304 # 1 << 22
global rand
rand = (a * rand + c) % m
return rand
#rand = 1
其输出序列周期是 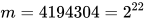
我们来看下这个 LCG 生成的伪随机二值图

看上去也挺不错的。我们很容易证明一个输出序列周期为 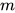 的 LCG,其输出是均匀分布在 [0, m - 1] 上。因为在一个周期内,同一个数只会出现一次,而总共只有
的 LCG,其输出是均匀分布在 [0, m - 1] 上。因为在一个周期内,同一个数只会出现一次,而总共只有 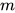 个数,所以 [0, m
- 1] 范围内的每一个整数各出现一次。但如果我们把范围缩小,会发现在周期的不同位置,不同大小的数出现分布有显著差别。现在我们可以继续看下大尺寸图像的效果
个数,所以 [0, m
- 1] 范围内的每一个整数各出现一次。但如果我们把范围缩小,会发现在周期的不同位置,不同大小的数出现分布有显著差别。现在我们可以继续看下大尺寸图像的效果

仔细看图,会发现有明显的条带,这是为什么——在图大小为 1024 * 1024 = 1048576 小于该 LCG 的周期 4194304 的情况下。事实上,这种规律性并不是由周期太短(B1)而导致的,而是序列相关(B2)导致——当 m 为 2 的幂时,LCG 输出值很容易保持高位不变,而连续在低位变化。在这个前提下,当我们把它归一化,比如除以 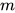 ,容易得到一串连续的 0 或者 1。一个更加著名的例子是 RANDU - Wikipedia
,容易得到一串连续的 0 或者 1。一个更加著名的例子是 RANDU - Wikipedia
所以很多现代编程语言标准库中的 PRNG 并不使用 LCG,比如 Python 的 random 库中使用的是 Mersenne Twister 。即使使用 LCG 作为 PRNG,也会做适当改进,比如 Java 的 Random 库中 next 方法使用 64 位整型参与计算,最后状态保留后 48 位(如果返回 int,则返回 48 位中的高 32 位)
5 更多 PRNG
比如上文提到的 Mersenne Twister,Python 使用它作为 Random 库的 PRNG,于 1997 年提出。其有巨大的周期 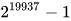 (B1),虽然我们已经知道长周期并不一定代表一个好的 PRNG,但是短周期必然不好。 Mersenne Twister 改进了朴素 LCG 中的统计特征方面的缺陷(A2 / B2),且和
LCG 一样高效(B3)
(B1),虽然我们已经知道长周期并不一定代表一个好的 PRNG,但是短周期必然不好。 Mersenne Twister 改进了朴素 LCG 中的统计特征方面的缺陷(A2 / B2),且和
LCG 一样高效(B3)

关于 Mersenne Twister 的更多信息,包括实现,参考
Permuted congruential generator(PCG),其包括一系列变种,统称为 PCG Family,其 2014 年才被提出。PCG 具有极其良好的特性,可以拥有任意大的周期;良好的统计特性(比 Mersenne Twister 更好,注 6);高效的计算;同时 PCG 的不可预测性也较前面所说的 PRNG 更好(虽然并未达到 CSPRNG 标准)。PCG Family 应该是目前综合表现最好的 PRNG 之一。

关于 PCG family 的更多信息,参考 PCG, A Family of Better Random Number Generators
其余更多 PRNG,参考 List of random number generators - Wikipedia
6 参考阅读
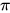 是一个好的 PRNG 么,类似的还有其他无理数
是一个好的 PRNG 么,类似的还有其他无理数

一个关于洗牌算法问题的小故事
When Random Isn't Random Enough: Lessons from an Online Poker Exploitwww.lauradhamilton.com
War3 录像使用 PRNG 的确定性,来重演整个伪随机过程
《魔兽争霸》的录像,为什么长达半小时的录像大小只有几百 KB?www.zhihu.com
随机数生成的 Wiki
Random number generationen.wikipedia.org
注 1:事实上掷骰子得到的数并不会严格均匀分布,甚至这个过程是不是严格意义上的随机也有很多不同的意见
注 2:初始状态的确定可能会引入一些随机性(随机种子),如果从不同的角度进行理解,PRNG 的一项功能是将初始状态的随机性进行扩散
注 3:计算机内部可能内置其他物理设备,用以搜集诸如外部热噪声,或一些电磁现象用以生成随机数,但是相对而言,还是较慢。可以参考 Hardware random number generator - Wikipedia
注 4: 这段图片生成代码如下
#pip install image
from PIL import Image
len = 127 #这个长度根据需要调整,建议根据 prng 周期来选择
img = Image.new('1', (len, len))
pixels = img.load()
for i in range(img.size[0]):
for j in range(img.size[1]):
#将实现 prng 归一化,或者将 if 条件改下
pixels[i, j] = 0 if prng() > 0.5 else 1
img.show()
注 5:关于参数选择可以参考 Linear congruential generator - Period length
注 6:Mersenne Twister 并没有通过 TestU01 的所有测试,而 PCG 通过了,TestU01 是一个软件库,提供了一系列用于 PRNG 的统计测试
注 7:PCG 实现可以通过 randomstate 库获得,randomstate 1.13.3