数据结构--二叉堆&优先队列

    优先队列，顾名思义，就是允许优先级高的元素先出队，优先级低的元素后出队。它与普通队列FIFO（先进先出）的特性不同，元素的出队顺序并不受入队顺序的影响，而是允许我们自定义元素的优先级（排序）来决定出队顺序。如果按照删除元素的策略划分，我们可以用如下方式理解栈、普通队列、优先队列的特性：

• 栈：最新的元素先出栈；（LIFO）
• 普通队列：最老的元素先出队；（FIFO）
• 优先队列：最大/小的元素先出队；

    优先队列的应用场景很广，比如任务调度使用优先队列存放待执行的任务，按照执行时间的先后顺序排序，从而保证先到达执行时间的任务先执行。再比如使用Cache时尝尝涉及到淘汰算法，根据元素的访问的活跃程度或者在缓存中的存放时间，决定优先淘汰哪些元素，这时也可以使用优先队列存放元素。
    优先队列与栈、普通队列相类似，也包含两个核心操作：插入元素，删除元素。栈的插入/删除都是在栈顶完成，普通队列的插入/删除分别在队尾、队首进行，二者都只是针对最多1个元素进行操作，因而效率都是 。优先队列的插入或者删除操作由于先要按优先级查找元素，因而插入和删除的效率并不能都达到，需要在实现时进行权衡取舍。现在假如我们考虑使用数组实现优先队列，可能的做法如下：

• 牺牲插入效率，提升删除效率：使用有序数组，在插入时，对元素进行排序，使得优先级越高的元素越靠近队首，每次删除时，删除队首元素；此时，插入平均效率为，而删除平均效率为；

• 牺牲删除效率，提升插入效率：使用无须数组，在插入时，将元素放在队尾，每次删除时，遍历查找优先级最高的元素删除；此时，插入平均效率为，删除效率为；

      使用上面方式实现优先队列，比较简单，应对小规模问题是可以的，但是如果对于元素数量较大的场景，则两个操作中可能有一个会成为瓶颈。为了能够保持较高的插入/删除效率，常用堆来实现优先队列，它能够保证插入/删除的平均效率都在，堆的实现有很多种，此处我们讨论最简单的一种：二叉堆。

什么是二叉堆？

堆有序：假定有一棵二叉树，它的父节点的值总是大于等于2个子节点的值，则此时的二叉树称为堆有序。
    在堆有序的二叉树中，每个节点都小于等于它的父节点。因而，在任意节点向上的路径总能得到一列非递减节点；任意节点向下的路径总能得到一列非递增的节点；此时可以保证从根节点到二叉树的每一个分支都是有序的，且根节点是值最大的节点。
    堆有序并不需要保证同一层级兄弟节点的有序性，仅需要保证从根节点到每一个叶子节点路径的有序性即可。即从根节点到每个叶子节点的路径单调递减。

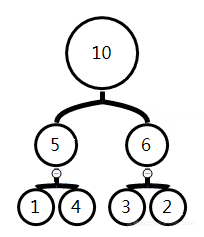
上图是一颗堆有序的二叉树，每一条二叉树的分支都是有序的：
10 > 5 > 1
10 > 5 > 4
10 > 6 > 3
10 > 6 > 2

完全二叉树：若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。一颗包含N个节点的完全二叉树，高度为。完全二叉树可以使用数组实现，树中的第k个元素的父节点为k/2，2个子节点分别为2k、2k+1，因而可以根据元素所在的位置计算出父子节点的位置，在树中移动元素时，仅需根据索引交换元素即可，而不需要借助指针，从而保证了操作的高效。

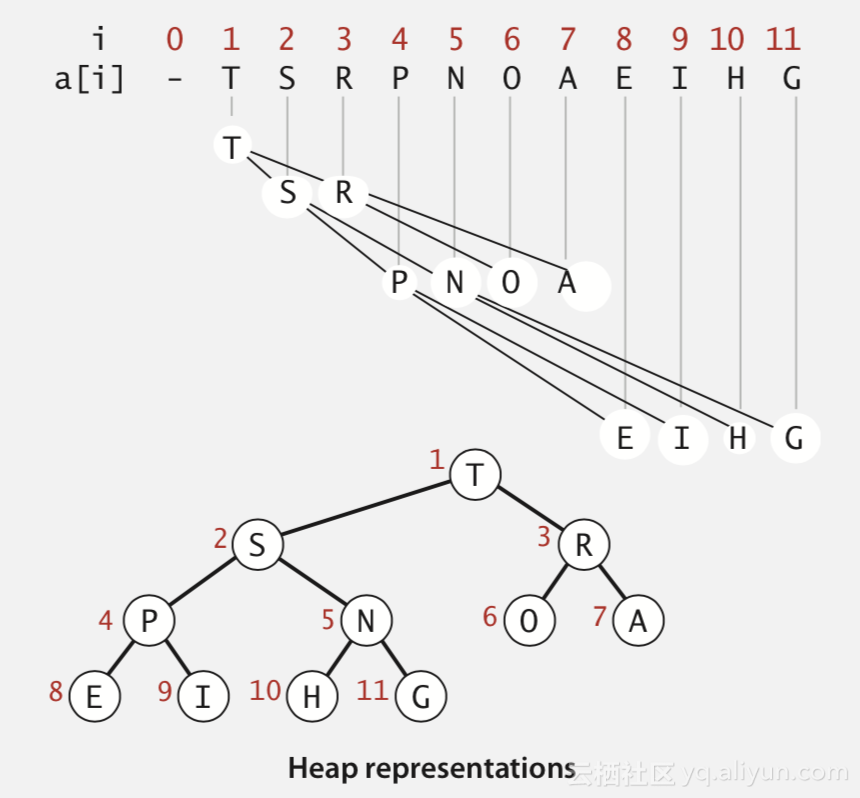
二叉堆：堆有序的完全二叉树。由于完全二叉树父子节点的索引可以根据位置计算出来，因而二叉堆可以按顺序逐层存放到数组中，如上图。二叉堆中处于k位置的元素，其父节点在数组中的位置是k/2，两个子节点的位置是2k，2k+1。比如上图中元素N在数组中的位置是5，则父节点S的索引是5/2=2，子节点H的索引为25=10，子节点G的索引为25+1=11，完全符合规律。

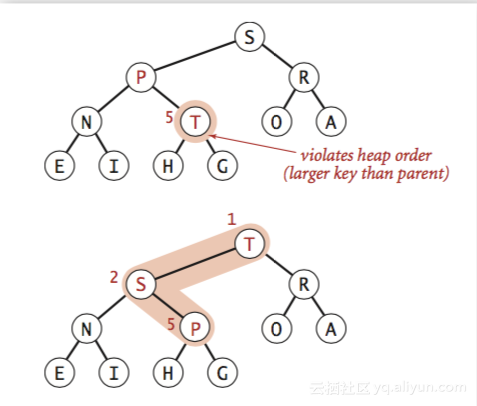
堆有序化：当新增或者删除二叉堆中的节点时，需要通过比较交换，使得节点处于一个合适的位置，同时这个过程叫做堆有序化。比如上图中，T > P > S，因而T先跟P交换，再跟S交换，最后变为根节点，整个二叉堆变为堆有序状态。

思考：为什么二叉堆在数组中的索引要从1开始？
答：为了满足根据元素所在位置查找父子节点的规律；二叉堆中处于k位置的元素，其父节点在数组中的位置是k/2，两个子节点的位置是2k，2k+1。如果索引从0开始，则规律有所改变，父节点位置是(k-1)/2，两个子节点的位置是2k+1，2k+2。

二叉堆实现优先队列的思路

首先考虑优先队列的两个核心操作的实现思路：

删除元素：自上而下的堆有序化（下沉）
使用二叉堆实现优先队列，每次删除元素时，因为根节点保存着最大的元素，因而只需要删除根节点，此时需要从堆中选出最大的元素作为新的根节点，因为使用数组存放二叉树，为保证数组元素的连续，通常先将数组末尾的元素放在根节点的位置，然后通过与子节点的比较交换，自上而下进行移动，最终落在一个合适的位置，此时的二叉堆也保持了堆有序的状态。

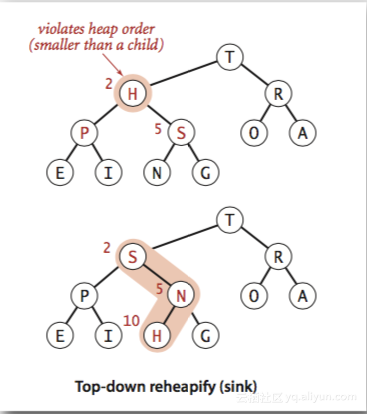
插入元素：自下而上的堆有序化（上浮）
当向二叉堆中插入元素时，需要先将元素放到数组末尾，然后通过与父节点的比较交换，自下而上的移动，最终放到一个合适的位置，此时的二叉堆也保持了堆有序状态。

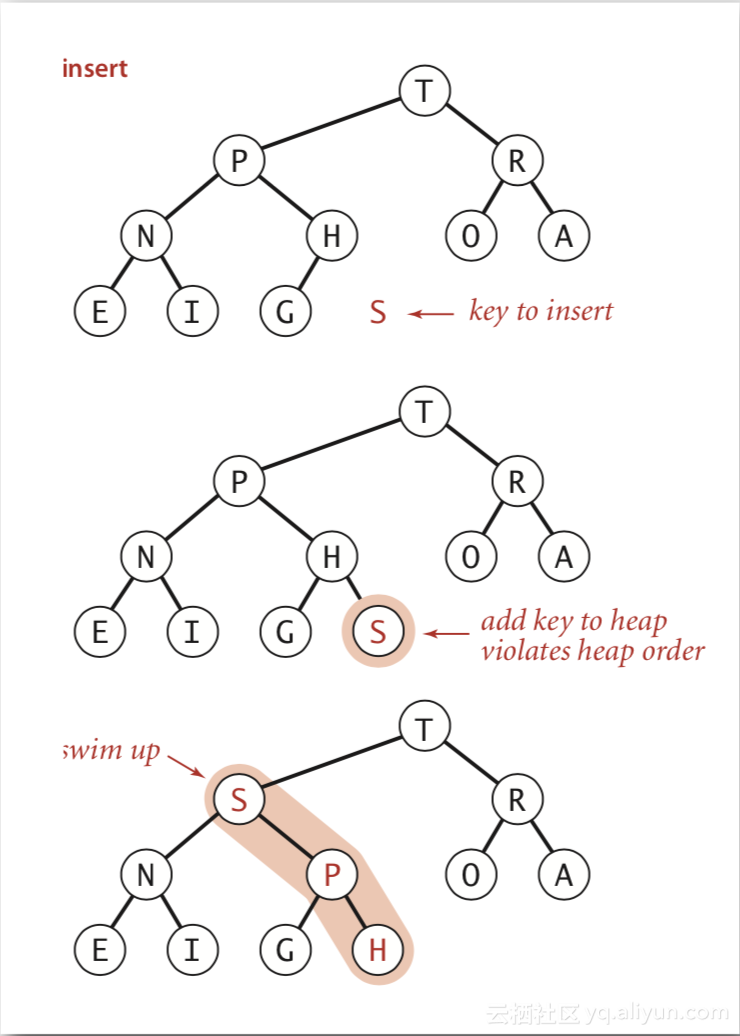
如上图所示，按照字母顺序组织的二叉堆。通过数组存放元素顺序如下：

T P R N H O A E I G

当新插入元素S时，会将S放入到数组的末尾，此时数组中元素顺序如下：

T P R N H O A E I G S

因为S > H > P，因而经过2次交换后，二叉堆变为有序状态，此时数组中元素顺序如下：

T S R N P O A E I G H

实现4个基本操作

实现上面的步骤需要4个基本操作：
比较（less）：比较两个元素的大小；
交换（exch）：交换两个元素在数组中的位置；
上浮（swim）：通过比较和交换，自下而上的移动元素，使其到达合适的位置；
下沉（sink）：通过比较和交换，自上而下的移动元素，使其达到合适的位置；

实现代码如下：

public class MaxPQ<Key extends Comparable<Key>> implements Iterable<Key> {

    /**
     * 存放堆元素的数组
     */
    private Key[] arr;

    /**
     * 堆中元素的数量
     */
    private int size;

    /**
     * 比较器，设定元素比较规则
     */
    private Comparator<Key> comparator;

    /**
     * 上浮
     */
    private void swim(int k) {

        while (k > 1 && less(k / 2, k)) {
            exch(k / 2, k);
            k = k / 2;
        }

    }

    /**
     * 下沉
     */
    private void sink(int k) {

        while (2 * k <= size) {

            int j = 2 * k;
            // 找出两个子节点中较大的节点
            if (j < size && less(j, j + 1)) {
                j++;
            }

            // 如果当前节点大等于子节点，则位置合适，跳出循环
            if (!less(k, j)) {
                break;
            }

            // 交换元素
            exch(k, j);
            // 更新元素位置，进入下一轮迭代
            k = j;
        }
    }

    /**
     * 比较
     */
    private boolean less(int i, int j) {

        // 若未指定比较器，则按照默认规则比较
        if (null == comparator) {
            return arr[i].compareTo(arr[j]) < 0;
        }

        // 若指定比较器，则使用比较器比较
        return comparator.compare(arr[i], arr[j]) < 0;
    }

    /**
     * 交换
     */
    private void exch(int i, int j) {
        Key tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
    
    ... ...
}

实现插入、删除操作

    我们按照上述实现思路，可以很方便的根据基本操作组合实现插入和删除操作，代码如下：

public class MaxPQ<Key extends Comparable<Key>> implements Iterable<Key> {

    ... ...

    /**
     * 插入元素
     */
    public void insert(Key value) {
        // 在数组末尾存放新增元素，增大size
        arr[++size] = value;
        // 将元素上浮到合适的位置
        swim(size);
    }


    /**
     * 删除最大值
     */
    public Key delMax() {
        // 获取最大值
        Key max = arr[1];
        // 将数组末尾元素换至根节点，同时减小size
        exch(1, size--);
        // 将根节点元素下沉到合适位置
        sink(1);
        // 清空引用，防止内存泄露
        arr[size + 1] = null;
        return max;
    }
    
    ... ...
}

初始化、状态获取操作实现

    上面实现了优先队列的核心内容，下面来完善优先队列的初始化及其它辅助操作：包括构造器的实现，通过empty()和size()判断队列中元素的数量... ...代码如下：

    public MaxPQ() {
        this(1);
    }

    /**
     * 指定arr的初始容量
     */
    public MaxPQ(int initialCapacity) {
        // 索引从1开始，因而数组长度+1
        arr = (Key[]) new Comparable[initialCapacity + 1];
        size = 0;
    }

    /**
     * 指定容量和比较器
     */
    public MaxPQ(int initialCapacity, Comparator<Key> comparator) {
        this.comparator = comparator;
        arr = (Key[]) new Comparable[initialCapacity + 1];
        size = 0;
    }

    /**
     * 指定比较器
     */
    public MaxPQ(Comparator<Key> comparator) {
        this(1, comparator);
    }

    /**
     * 通过传入arr创建优先队列
     */
    public MaxPQ(Key[] arr) {

        size = arr.length;
        this.arr = (Key[]) new Comparable[size + 1];
        for (int i = 0; i < size; i++) {
            this.arr[i + 1] = arr[i];
        }

        // 从倒数第二层开始sink，因为叶子节点不需要sink
        for (int k = size / 2; k >= 1; k--) {
            sink(k);
        }
    }
    
    /**
     * 返回队列中的最大值
     */
    public Key max() {

        if (isEmpty()) {
            throw new NoSuchElementException("priority queue is empty");
        }

        return arr[1];
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public int size() {
        return size;
    }

动态扩缩容

    优先队列基于数组实现，由于数组的长度固定，存放元素数量有上限，当插入元素数量到达数组上限时，需要扩容数组长度；当删除元素，使得数组长度空余许多时，需要减少数组长度。扩缩容的时机：

• insert时，如果size == arr.length-1，此时数组已满，需要扩容；
• delMax时，如果size == (arr.length-1)/2，此时需要缩容；

实现代码如下：

    /**
     * 动态扩容
     */
    private void resize(int capacity) {
        assert capacity > size;

        // 创建新数组，拷贝原数组元素
        Key[] newArr = (Key[]) new Comparable[capacity];
        for (int i = 1; i <= size; i++) {
            newArr[i] = arr[i];
        }

        // 更新数组引用
        arr = newArr;
    }
    
    /**
     * 插入元素
     */
    public void insert(Key value) {

        // 如果容量已满，则成倍扩容
        if (size == arr.length - 1) {
            resize(2 * arr.length);
        }

        // 在数组末尾存放新增元素，增大size
        arr[++size] = value;
        // 将元素上浮到合适的位置
        swim(size);
    }

    /**
     * 删除最大值
     */
    public Key delMax() {

        if (isEmpty()) {
            throw new NoSuchElementException("priority queue is empty");
        }

        // 获取最大值
        Key max = arr[1];
        // 将数组末尾元素换至根节点，同时减小size
        exch(1, size--);
        // 将根节点元素下沉到合适位置
        sink(1);
        // 清空引用，防止内存泄露
        arr[size + 1] = null;

        // 如果元素数量仅为数组长度的1/4，则数组缩容至原来的1/2；
        // 之所以缩容至原来的1/2而不是1/4，是因为索引0位置空缺，缩容1/4，可能少一个位置；
        if (size > 0 && size == (arr.length - 1) / 4) {
            resize(arr.length / 2);
        }

        return max;
    }

二叉堆的效率

    使用二叉堆实现优先队列的效率相比于本文开头讨论的方式要好很多。对于一个包含N个元素的优先队列，插入一个元素，最多进行次比较（最坏情况从末尾到根节点比较次+跳出循环条件1次）；删除最大元素，最多进行 次比较（最坏情况从根节点一直下沉到叶子节点，下沉次，每一轮进行2次比较，共次）；

最大堆与最小堆

    上面讨论的二叉堆实现，是约定父节点大于等于子节点，因而根节点存放的元素最大，这时的堆实现称为最大堆；如果将定义反过来，约定父节点小于等于子节点，此时根节点存放的元素最小，则称为最小堆。最大堆和最小堆实现的差异主要在于比较策略的不同，实现时，只要改变less比较符的方向或者将Comparator比较顺序翻转（调用reverseOrder()），即可实现最大堆和最小堆实现的转变。

一个降序排列的数组一定是一个最大堆；而一个升序排列的数组一定是一个最小堆；

判断一个数组是否是最大堆

判断从索引k开始的子二叉树是否是最大堆。通过递归实现：

    private boolean isMaxHeap() {
        return isMaxHeap(1);
    }

    private boolean isMaxHeap(int k) {

        if (k > size) {
            return true;
        }

        int left = 2 * k;
        int right = 2 * k + 1;

        if (left <= size && less(k, left)) {
            return false;
        }

        if (right <= size && less(k, right)) {
            return false;
        }

        // 递归判断
        return isMaxHeap(left) && isMaxHeap(right);
    }

测试用例

/**
 * MaxPQ测试
 */
public class MaxPQTest {

    private int[] testArr = {9, 7, 10, 8, 5, 2, 3, 4, 6, 1, 0};

    @Test
    public void insert() throws Exception {

        MaxPQ<Integer> maxPQ = new MaxPQ<>();
        for (int i : testArr) {
            maxPQ.insert(i);
        }

        Assert.assertTrue(maxPQ.isMaxHeap());

        for (int i : maxPQ) {
            System.out.println(i);
        }
    }

    @Test
    public void delMax() throws Exception {

        Integer[] arr = new Integer[testArr.length];
        for (int i = 0; i < testArr.length; i++) {
            arr[i] = testArr[i];
        }

        MaxPQ<Integer> maxPQ = new MaxPQ<>(arr);
        Assert.assertTrue(maxPQ.isMaxHeap());

        Assert.assertEquals(10, (int) maxPQ.delMax());
    }

    @Test
    public void max() throws Exception {

        MaxPQ<Integer> maxPQ = new MaxPQ<>(10);
        for (int i = testArr.length - 1; i >= 0; i--) {
            maxPQ.insert(testArr[i]);
        }
        Assert.assertTrue(maxPQ.isMaxHeap());

        Assert.assertEquals(10, (int) maxPQ.max());
    }

    @Test
    public void isEmpty() throws Exception {

        MaxPQ<Integer> maxPQ = new MaxPQ<>(10);
        Assert.assertTrue(maxPQ.isEmpty());

        maxPQ.insert(1);
        Assert.assertFalse(maxPQ.isEmpty());
    }

    @Test
    public void size() throws Exception {

        MaxPQ<Integer> maxPQ = new MaxPQ<>(5);
        for (int i = testArr.length - 1; i >= 0; i--) {
            maxPQ.insert(testArr[i]);
        }
        Assert.assertTrue(maxPQ.isMaxHeap());

        Assert.assertEquals(testArr.length, maxPQ.size());
    }

    @Test
    public void iterator() throws Exception {

        MaxPQ<Integer> maxPQ = new MaxPQ<>();
        for (int i = testArr.length - 1; i >= 0; i--) {
            maxPQ.insert(testArr[i]);
        }
        Assert.assertTrue(maxPQ.isMaxHeap());

        int i = 10;
        Iterator<Integer> iterator = maxPQ.iterator();
        while (iterator.hasNext()) {
            Assert.assertEquals(i--, (int) iterator.next());
        }
    }

    @Test
    public void forEach() throws Exception {

        MaxPQ<Integer> maxPQ = new MaxPQ<>();
        for (int i = testArr.length - 1; i >= 0; i--) {
            maxPQ.insert(testArr[i]);
        }
        Assert.assertTrue(maxPQ.isMaxHeap());

        List<Integer> list = new ArrayList<>();
        maxPQ.forEach(list::add);

        Assert.assertEquals(0, (int) list.get(testArr.length - 1));
        Assert.assertEquals(10, (int) list.get(0));
    }
}

总结

1）基于二叉堆实现的优先队列，插入和删除操作效率都能够达到，使得入队和出队效率相对平衡，但并不一定在所有场景都是最优的方法。比如，对于插入较多，删除较少的场景，可以考虑使用无序数组实现优先队列，是的插入的效率为；而对于删除较多而插入较少的场景，可以考虑使用有序数组实现，从而使得删除效率为 。
2）一个降序排列的数组一定是一个最大堆；而一个升序排列的数组一定是一个最小堆；
3）通过insert操作copy一个二叉堆，性能是；
4）二叉堆适合于在大规模数据集中求解TopN的问题，对于求解MaxTopN，可以考虑使用大小为N的最小堆，每次处理都包含一次sink（插入当前元素）和swim（删除最小元素）操作，是的最大的元素逐渐沉淀下来；反之，对于求解MinTopN，可以考虑使用大小为N的最大堆，使得最小的元素逐渐沉淀下来。
5）二叉堆推而广之，我们可以使用多叉堆来实现优先队列，从而保证 的插入和删除效率，其中m为堆中每个节点可以包含的最大子节点数。比如，使用基于数组的完全三叉树构造三叉堆，对于数组中的1到N个元素，位置k的父节点索引在(k+1)/3，子节点索引分别在3k-1，3k，3k+1的位置。此时数的高度是，因而插入和删除效率均为。

参考

算法（第4版）2.4节-优先队列
coursera算法视频课程