起手诗
从今天起,做一个牛X的人,早起,健身,修炼算法
从今天起,关心代码质量,我有一个梦想,朝九晚五,年薪百万
从今天起,和每一个亲人通信,告诉他们我的决心
那成功的天使告诉我的
我想告诉每一个人
给每一个文件、每一个变量取一个温暖的名字
陌生人,我也为你祝福
愿你有一个灿烂的前程
愿你的头发不再减少
愿你明天仍是公司栋梁
而我,只愿朝九晚五,年薪百万
前言
书接上文从今天起,每天详解一道算法题,今天实现一个二叉查找树。
基本概念
二叉查找树是二叉树的一种特殊情况,二叉查找树的左边节点的值总是比右边的小,先看下定义:
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉查找树。
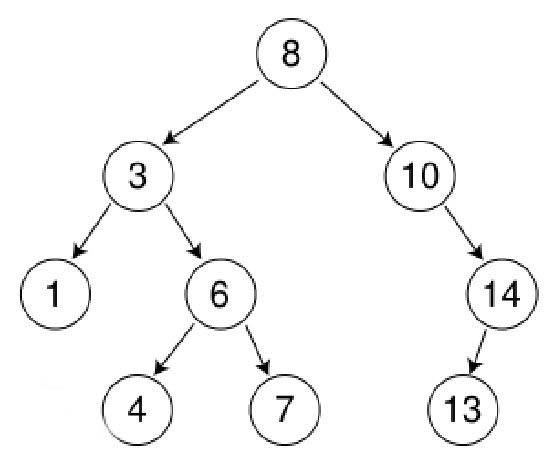
节点:包含一个数据元素及若干指向子树的分支;
根节点:第一层的节点(图中的8);
叶子节点:结点的子树的根称为该结点的叶子节点,这是一个相对概念;
结点层:根结点的层定义为1;根的孩子为第二层结点,依此类推;
树的深度:树中最大的结点层;
结点的度:结点子树的个数(二叉树为2);
树的度:树中最大的结点度(二叉树为2);
代码实现
实现二叉树,先要实现上面最重要的一个概念--节点:
它有三个属性,值、左节点的指针、右节点的指针:
class Node {
constructor(data, left, right) {
this.value = data
this.left = left
this.right = right
}
show(){
return this.data
}
}
下面我们实现二叉查找树的类:
我们可以想向到它应该有一个根节点,还应该有一些操作该类的方法,我会分别解释,先看代码(为了避免代码太长,我把各个方法分开写了,他们应该都在BST类里的):
insert方法:
该方法负责向该二叉树中插入一条数据,实现的思路是:
1、通过Node类创建包含该条数据的一个节点;
2、判断如果该实例的根节点root为null,则把这个节点设置为根节点;
3、如果根节点不为null,则创建一个指向当前节点的指针(第一次指向根节点),然后比较data是否大于当前节点的data;
4、如果小于当前节点的data,则说明这个节点应该往左边放,否则说明应该往右边放;
5、通过循环比较,最终当前节点会找到null,这时候把新节点插入到这里(也就是让当parentNode的子节点指向新节点);
class BST {
constructor() {
this.root = null
}
insert(data) {
let newNode = new Node(data, null, null)
if (root == null) {
this.root = newNode
} else {
let currentNode = this.root
let parentNode
while (true) {
parentNode = currentNode
if (data < currentNode.data) {
currentNode = currentNode.left
if (currentNode == null) parentNode.left = newNode
break
} else {
currentNode = currentNode.right
if (currentNode == null) parentNode.right = newNode
break
}
}
}
}
}
遍历方法:
树的遍历分为3种类型:中序、先序、后序,其中“中”、“先”、“后”指的是访问根节点的时机。
下面代码中的each方法中有三个console,从上至下他们分别对应先序、后序、中序。他们分别代表访问根节点(2)的时机。也就是一个在最先,一个在最后,一个在中间。
each(node) {
node = node || this.root
//console.log(node.data) // 2,1,3
if (node.left) this.each(node.left)
//console.log(node.data) // 1,2,3
if (node.right) this.each(node.right)
//console.log(node.data) // 1,3,2
}
查找最大最小值
这两个方法比较简单,最大值就是遍历右子树,找到最后一个;最小值就是遍历左子树找到最后一个
注:max和min方法有参数,这是为了查找制定节点的最大最小值,下面的remove方法中用到了min方法查找制定节点的最小值
max(node) {
let currentNode = node || this.root
while (currentNode.right) {
currentNode = currentNode.right
}
return currentNode.data
}
min(node) {
let currentNode = node || this.root
while (currentNode.left) {
currentNode = currentNode.left
}
return currentNode.data
}
查找给定值的节点
has方法和上面的insert方法的思路类似,都是创建一个指针指向根节点,比较传入的data值,如果比根节点大就把指针向右移,否则向左。
一旦找到相等的值就返回ture,如果遍历到最后一个节点都没有找到,返回false。
has(data) {
let currentNode = this.root
while (currentNode) {
if (data == currentNode.data) {
return true
} else if (data < currentNode.data) {
currentNode = currentNode.left
} else {
currentNode = currentNode.right
}
}
return false
}
删除给定值的节点
删除方法相对较复杂,思路为:
1、定义remove方法,方法中把根节点更改为一个递归方法removeNode的返回值
2、removeNode是一个被删除了制定节点的新树,它的实现需要考虑以下几种情况:
a:如果输入节点为null,则返回null
b:如果data与node的data相等,说明这个节点就是需要被删除的节点(这种情况又分为几种情况,下面单独说)
c:如果data比node的data小,则说明需要删除的节点在node的左边,那么就需要递归它左边这个节点,直到找到相等的或者null
d:如果data比node的data大,思路同c
接下来说b(命中相等节点)的情况:
1、如果这个节点没有子节点,那么直接删除即可
2、如果这个节点只有一个节点,那么它的这个子节点应该取代它的位置(代码中第二、三行注释下的代码)
3、如果这个节点有左右两个节点,那么我们找到它的右子树的最小值minData,这个节点的值就应该为minData,同时让它的右子树为它之前的右子树(删除最小值之后的)。
remove(data) {
this.root = removeNode(this.root,data)
}
removeNode(node, data) {
if (node == null) {
return null
}
if (data == node.data) {
//没有节点,返回null
if (node.left == null && node.right == null) {
return null
}
//没有左节点,右节点替换当前节点
if (node.left == null) {
return node.right
}
//没有右节点,左节点替换当前节点
if (node.right == null) {
return node.left
}
//左右节点都存在
let minData = this.min(node.right)
node.data = minData
node.right = this.removeNode(node.right, minData)
return node
} else if (data < node.data) {
node.left = this.removeNode(node.left, data)
return node
} else if (data > node.data) {
node.right = this.removeNode(node.right, data)
return node
}
}
参考资料
《数据结构与算法-javascript描述》
《学习javascript数据结构与算法》