我们可以在网页中轻易地展示图片或其他平面形状。然而,当要展示 3D 模型时,事情就不那么简单了,因为三维空间比二维空间更复杂。为了实现 3D 效果,我们可以使用专门的技术和库,如 WebGL 和 Three.js。
然而,如果你只是想展示一些基本形状时,如立方体,那么这些技术就显得大材小用了。另外,使用它们并不会帮助你理解其工作原理,或解答如何在平面中显示 3D 形状的疑问。
我编写这篇教程的目的是:阐述如何在 web 中构建一个简单的 3D 引擎(无 WebGL)。我们将首先学习如何存储 3D 模型,然后学习如何在两种不同视图(正视图和透视图)中展示这些形状。
保存和转换3D模型
所有形状都是多面体
虚拟世界与现实的最大不同是:没有东西是连续的,即所有东西都是离散的。例如,你无法在屏幕上显示一个完美的圆。你只能以一个正多边形表示圆:边越多,圆就越“完美”。
同理,在三维空间,每个 3D 模型都等同于一个 多面体(即 3D 模型只能由不弯曲的平面组成)。当我们讨论一个本身就是多面体(如立方体)的模型时并不足以为奇,但当我们想展示其它模型时,如球体时,就需要记住这个原理了。
保存一个多面体
想要保存一个多面体,就需要运用数学知识将其表示出来。你肯定在上学期间学过一些基本的几何知识。以正方形为例,你需要定义 ABCD 四个标识符,它们分别代表正方形的每个直角。
我们的 3D 引擎也一样。我们从保存模型的每个顶点开始。然后,模型的每个面都会被这些顶点所标注。
我们需要正确的结构体去表示顶点。因此,我们创建一个类去存储顶点的坐标。
var Vertex = function(x, y, z) {
this.x = parseFloat(x);
this.y = parseFloat(y);
this.z = parseFloat(z);
};现在我们可以像下面这样创建顶点了。
var A = new Vertex(10, 20, 0.5);接着,我们创建一个类去表示多面体。我们以立方体为例。下面是该类的定义,后面会有相应的解释。
var Cube = function(center, size) {
// Generate the vertices
// 生成多个顶点
var d = size / 2;
this.vertices = [
new Vertex(center.x - d, center.y - d, center.z + d),
new Vertex(center.x - d, center.y - d, center.z - d),
new Vertex(center.x + d, center.y - d, center.z - d),
new Vertex(center.x + d, center.y - d, center.z + d),
new Vertex(center.x + d, center.y + d, center.z + d),
new Vertex(center.x + d, center.y + d, center.z - d),
new Vertex(center.x - d, center.y + d, center.z - d),
new Vertex(center.x - d, center.y + d, center.z + d)
];
// Generate the faces
// 生成面
this.faces = [
[this.vertices[0], this.vertices[1], this.vertices[2], this.vertices[3]],
[this.vertices[3], this.vertices[2], this.vertices[5], this.vertices[4]],
[this.vertices[4], this.vertices[5], this.vertices[6], this.vertices[7]],
[this.vertices[7], this.vertices[6], this.vertices[1], this.vertices[0]],
[this.vertices[7], this.vertices[0], this.vertices[3], this.vertices[4]],
[this.vertices[1], this.vertices[6], this.vertices[5], this.vertices[2]]
];
};通过这个类,我们只需指定中心和边长就可创建一个虚拟的立方体。
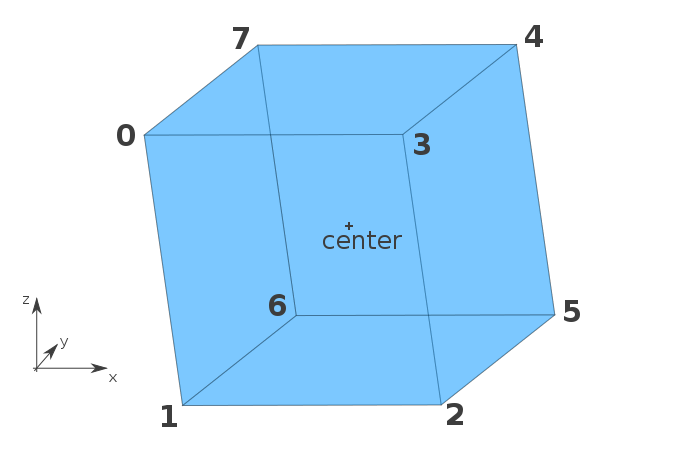
var cube = new Cube(new Vertex(0, 0, 0), 200);Cube 类的构造函数先通过指定的中心位置生成立方体的顶点。通过下面的模型可更清晰地看到,我们创建的8个顶点的位置:
然后,我们列出了面。由于每个面都是正方形,所以需要为每个面指定4个顶点。这里我选择用一个数组表示一个面,当然,你也可以创建一个专门的类表示面。
当我们是通过 4 个顶点(已存储在 this.vertices[i])创建一个面时,就不需要再指定这面的位置。而且,下面有另外一个理由驱使我这样做。
默认情况下,JavaScript 会尽可能少地占用内存。因此,通过参数传进函数的对象或数组(数组也是对象)都不是副本,而只是引用。因此,我们在上面的例子中很好地做到这一点。
实际上,面上的每个顶点都含有 3 个数值(它们的坐标)。假如我们将面上的顶点以副本进行存储,这无疑会使用大量多余的内存。这里,我们使用了引用的方式:坐标都仅需保存一次。通过引用(而非副本的方式),每个顶点会被 3 个面共同使用,因此内存只需原来的三分之一左右。
我们需要三角形吗?
Why do 3D engines primarily use triangles to draw surfaces? 这个提问说道:三角形肯定不会是立体的,但超过3点的面就可以是立体的,因此不能得到渲染,除非转为三角形。具体可看看这个提问。
如果我们曾经使用过 3D(如 Blender 软件或 WebGL 库),可能已经听过三角形。这里,我们选择不使用三角形。
之所以这样选择,是因为这篇文章是以入门为主的,而且我们只会展示一些基本的形状,如立方体。使用三角形表示正方形无疑会让问题复杂化。
然而,如果你计划构建一个更完整的渲染器,那么就需要了解这方面的知识了,一般来说,三角形是完美的。下面有两个主要理由支撑该说法:
- 纹理:出于一些数学方面的原因,想在面上展示图片就需要三角形;
- 不规则的面:三个顶点总会在同一个面上。然而,你可以不在该平面上添加第四个顶点,然后连接这四个顶点创建一个面。在这种情况下,为了能进行绘制,我们别无选择,只能将四边形切成两个三角形(可用一张纸试试!)。通过使用三角形,你能选择切开的位置。
操作多面体
这是保存引用(而不是副本)的另一优势。当我们因操作多面体而进行数值运算时,效率能提高3倍(备注:由于是引用,只需修改一处)。
为了理解当中的原因,让我们再次回忆我们的数学课。当你想平移一个正方形时,你不是真的去移动它。实际上,你只是移动四个顶点。
下面,我们将尝试上述的平移操作:我们无需理会面,只需为每个顶点进行相应的运算。这是因为面是由顶点的引用组成,面的坐标会自动更新。看看我们是如何移动上面所创建的立方体:
for (var i = 0; i < 8; ++i) {
cube.vertices[i].x += 50;
cube.vertices[i].y += 20;
cube.vertices[i].z += 15;
}渲染图像
目前,我们已懂得如何存储和操作 3D 对象了。现在就看看如何渲染它们!在这之前,为了明白我们将要做的事,需要普及一些理论知识。
投影
目前,我们存储的是 3D 坐标。然而,屏幕只能显示 2D 坐标,因此我们需要一种将 3D 坐标转为 2D 的方式:在数学中,我们称之为投影。3D 转 2D 的投影是一个抽象的操作,由一个被称为虚拟摄像机的对象构成。该摄像机会将一个 3D 对象的坐标转为 2D 坐标,然后将其传输给渲染器,以在屏幕上进行显示。我们假设这台摄像机放置在 3D 空间的原点(即(0,0,0))。
在文章开头,我们通过三个数值 x,y和 z 表示坐标。但为了定义坐标,我们需要一个基础原则:z 是竖直坐标吗?它用来表示上/下位移的吗?这没有统一的答案,也没有约定,事实上,你可以选择任何你想要的。你唯一需要记住的是:在操作 3D 对象时,你必须保持一致,因为它决定了公式的定义。在这篇文章中,我选择的基本原则能在上述的立方体模型中看出:x 是从左向右,y 是从后向前(备注:我们是后,屏幕是前),z 是从下向上。
现在,我们知道该做什么了:为了显示三维空间上的坐标(x,y,z),我们需要将它们转换为二维空间的坐标(x,y):因为在平面中,只有转换后才能够进行显示。
不仅只有一个投影。更坏的是,有无数种不同的投影!在这篇文章中,我们会看到两种不同类型的,且在实际中最常见的投影。
如何渲染场景
在对对象进行投影前,让我们编写用于显示的函数。该函数接受一个对象数组作为参数,而 canvas 的上下文是用于渲染这些对象的,函数的其余部分则是将对象绘制在正确的位置上。
该数组包含了用于渲染的对象。这些对象必需能反映这样一件事:拥有一个名为 faces 的公有属性,该属性是一个存有该 3D 模型所有面的数组(如先前创建的立方体)。而这些面可以是任何类型的(正方形,三角形,或甚至是十二边形(如果你愿意)):面是一个保存着顶点的数组。
让我们看看该函数的实现代码,紧随其后的是解释:
function render(objects, ctx, dx, dy) {
// For each object
for (var i = 0, n_obj = objects.length; i < n_obj; ++i) {
// For each face
for (var j = 0, n_faces = objects[i].faces.length; j < n_faces; ++j) {
// Current face
var face = objects[i].faces[j];
// Draw the first vertex
// 绘制第一个顶点
var P = project(face[0]);
ctx.beginPath();
ctx.moveTo(P.x + dx, -P.y + dy);
// Draw the other vertices
// 绘制其余顶点
for (var k = 1, n_vertices = face.length; k < n_vertices; ++k) {
P = project(face[k]);
ctx.lineTo(P.x + dx, -P.y + dy);
}
// Close the path and draw the face
ctx.closePath();
ctx.stroke();
ctx.fill();
}
}
}该函数需要解释的部分应该是 project() 函数与参数 dx、dy 分别是什么。其余的语句基本无需解释,基本上是遍历对象,然后绘制每一面。
正如其名字所示,project() 函数是用于将 3D 坐标转为 2D 坐标的。它接收在 3D 空间的一个顶点,然后返回 2D 平面的顶点。下面是 2D 平面顶点的定义:
var Vertex2D = function(x, y) {
this.x = parseFloat(x);
this.y = parseFloat(y);
};我在这选择将 z 坐标重命名为 y,以保持 2D 几何学的传统约定,当然你也可以保持 z。
project() 的具体内容将在下一节看到:这取决于你选择的 project 类型。但无论它的类型是什么,render() 函数仍保持不变。
一旦拥有平面坐标,我们就能在 canvas 上进行渲染,顺便提了一个小技巧:我们没有绘制 project() 函数返回的实际坐标。
实际上,project() 函数返回了一个虚拟 2D 平面的坐标,但与 3D 空间的原点(0,0,0)相同。然而,我们想让该原点在 canvas(画布)的中心,这就是为什么我们将坐标进行平移:顶点 (0,0) 并不在画布的中心,但 (0 + dx, 0 + dy) 是。由于我们想将 (dx,dy) 放置在canvas中心,我们没有什么好的选择,就定义 dx = canvas.width / 2,dy = canvas.height / 2。
最后,还有一点需要说明的是: 为什么我们使用 -y 而不是直接使用 y?其实这是基于我们之前选择的基本原则之上:z 轴 是向上的。在我们这种情景中,顶点的 z 坐标若是正数,则表示向上移。然而,在 canvas 中,y轴是向下的:顶点的 y 坐标若是正数,则会向下移动。这就是为什么在当前情景下,定义的 z 坐标是与 y 坐标相反的。
现在理解 render() 函数了,是时候看看 project()。
正视图
让我们开始正交投影吧。这是最简单的一步了,因此很容易理解我们将要做的事情。
目前顶点有三个坐标值,但我们只想要两个。在这种情景下的最简单的处理方式是什么呢?移除其中一个坐标值。这也是我们在正视图中所做的事。我们将移除用于表示深度的 y 坐标值。
function project(M) {
return new Vertex2D(M.x, M.z);
}到目前为止,结合文章的所有代码进行测试:能运行!这是值得庆祝的一刻,你能在平面展示一个 3D 物体!
下面的线上案例正是实现的功能,而且它还能通过鼠标让这个立方体进行旋转哦。
线上 Demo: 3D Orthographic View by SitePoint (@SitePoint) on CodePen.
有时,我们就是需要一个正视图,因为他拥有正交投影的特点(不变形)。然而,这不是最自然的视图:我们肉眼所看到的视觉效果并不像这样。这就引出我们将要讲到的第二种投影:透视图。
透视图
透视图比正视图稍微复杂一点,因为我们需要进行一些运算。然而,这些运算并不复杂,你只需知道这么一件事:如何使用 截线定理(又称为平行截割定理,平行线分线段成比例定理)。
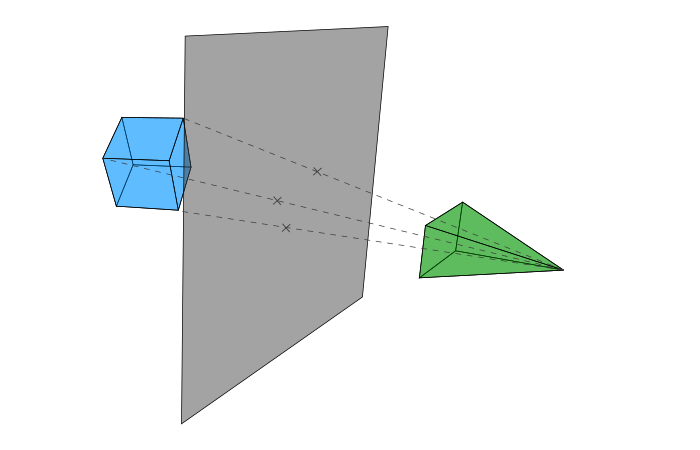
为了明白其中的原因,让我们看看正视图的模型。我们将点以正交的方式投影在平面上。
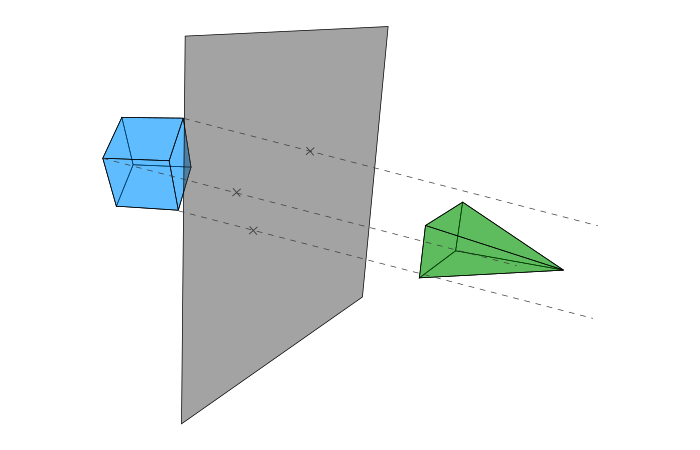
但在现实世界中,我们眼睛的行为更像以下这种模型。
接下来,我们要进行以下两个步骤:
- 连接原始顶点和摄像源;
- 投影是线与面的交点;
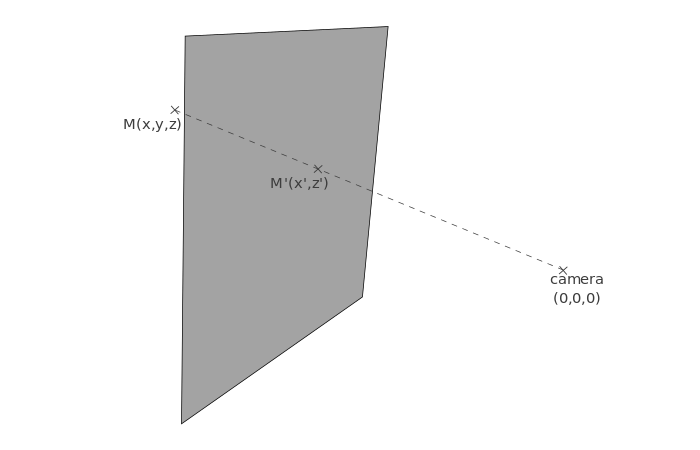
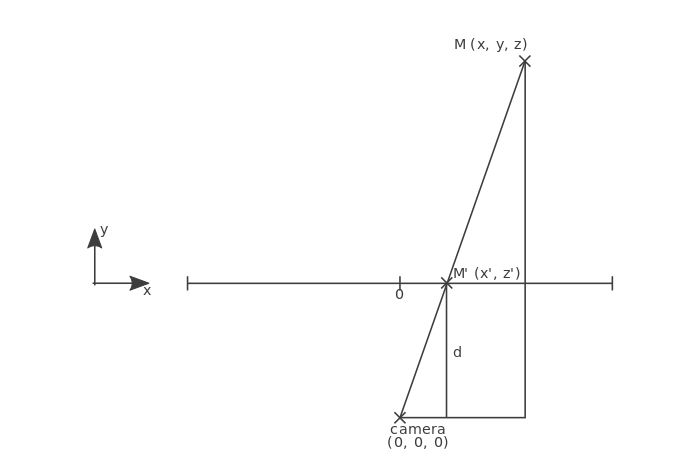
与正视图不同,平面的具体位置变得重要起来了:如果你将平面放置在远离摄像机的地方,效果就与平面靠近摄像机的效果不同。现在我们将其放置在距离摄像机距离为 d 的位置。
对于 3D 空间的顶点 M(x,y,z),我们需要算出其投影在平面上的 M' 点坐标 (x',z')。
在上述模型中,我们知道这些值:x, y 和 d。运用截线定理可得到该等式:x' = d / y * x。
同理,从侧面观察同一个模型,可得该等式:z' = d / y z。
现在我们能编写使用透视图的 project() 函数:
function project(M) {
// Distance between the camera and the plane
// 摄像机与平面的距离
var d = 200;
var r = d / M.y;
return new Vertex2D(r * M.x, r * M.z);
}该函数能在下面的线上案例进行测试。当然,你也能与立方体进行交互。
线上Demo:3D Perspective View by SitePoint (@SitePoint) on CodePen.
结束语
我们(非常基础)的 3D 引擎现在已经能展示任何 3D 模型了。但它仍有几处可以完善的地方。如我们能看到该模型的任何一面,甚至是背面。为了隐藏它,你可以实现 背面剔除(back-face culling)。
另外,我们没讲到纹理。目前,模型的每个面都是同一种颜色的。其实,我们无须修改太多即可添加纹理,如为对象添加一个颜色属性,然后绘制上去。你甚至可为每一面绘制一张图像。为了保持文章的简易,我并没有详细讲解这方面。
我们还可以进行其它操作。我们将摄像机放置在空间的中心,但你可以移动它(需在投影顶点前)。另外,未被摄像机拍摄到的顶点也被绘制出来了,这并不是我们想要的结果。裁剪平面(clipping plane)能修复这个问题(易于理解,但不容易实现)。
如你所见,3D 引擎到这里已经算完成了,这也是我自己的实现方式。你可以添加其它的类:如 Three.js 使用一个专门的类去管理摄像机和投影。另外,我们使用基本的数学知识去存储坐标,但如果你想创建一个更复杂的应用,例如:对于在一帧内旋转多个顶点的操作,目前的引擎很难拥有一个流畅的体验。为了优化这种情况,你需要一些更复杂的数学知识:齐次坐标(射影几何)和 四元数。
如果有人让你推荐前端技术书,请让他看这个列表 ->《经典前端技术书籍》2 赞 3 收藏 评论打赏支持我翻译更多好文章,谢谢!
打赏译者