欢迎访问集智主站:集智,通向智能时代的引擎
注意!
本文所有代码均可在集智原贴中运行调试(无需安装环境),请点击这里前往原贴
聚类:数以类聚
聚类所解决的问题
对于鸢尾花数据集,若已知有三类,但是不知道具体是哪三类,则可以尝试聚类算法:把采样划分至特征鲜明的不同组中。
K-平均聚类
聚类的标准和相应的算法多的很,最simple的聚类算法是K-平均(K-means)。
# 从Scikit-learn导入聚类和数据集两个模块
from sklearn import cluster, datasets
iris = datasets.load_iris()
X_iris = iris.data
y_iris = iris.target
# 创建聚类器对象,指定分组数量为3,并将结果每隔10个数据赋值予变量y_iris_k_means
k_means = cluster.KMeans(n_clusters=3)
k_means.fit(X_iris)
y_iris_k_means = k_means.labels_[::10]
# 分别输出聚类算法结果,与标签进行对比
print("K-means聚类结果:")
print(y_iris_k_means)
print("数据集原始标签:")
print(y_iris[::10])
# 从Scikit-learn导入聚类和数据集两个模块
from sklearn import cluster, datasets
iris = datasets.load_iris()
X_iris = iris.data
y_iris = iris.target
# 创建聚类器对象,指定分组数量为3,并将结果每隔10个数据赋值予变量y_iris_k_means
k_means = cluster.KMeans(n_clusters=3)
k_means.fit(X_iris)
y_iris_k_means = k_means.labels_[::10]
# 分别输出聚类算法结果,与标签进行对比
print("K-means聚类结果:")
print(y_iris_k_means)
print("数据集原始标签:")
print(y_iris[::10])
len(y_iris_k_means) == 15
导入cluster和datasets模块
创建数据集和聚类器对象cluset.KMeans()
结果每隔10个数据赋值予变量y_iris_k_means
与datasets自带的标签进行对比
警告: 算法无法保证能够还原真实准确的聚类(ground truth)。首先选择一个正确的分组数量就很难;其次算法对初始条件极其敏感,尽管Scikit-learn采取了若干措施以避免,但仍有陷入局部最小值的风险。
请勿对聚类结果作过度解读。
应用实例:量化矢量
广义上的聚类算法,尤其是K-Means可以看作是挑选一小部分范式以压缩信息量,这个问题也被称为量化矢量(vector quantization),可用于对图像做色调分离:
%matplotlib inline
import numpy as np
from sklearn import cluster
import matplotlib.pyplot as plt
# 导入科学计算库Scipy并缩写为sp
import scipy as sp
try:
# 创建face对象,设置为灰度
face = sp.face(gray=True)
except AttributeError:
from scipy import misc
face = misc.face(gray=True)
# 将图像转化为形如 (n_sample, n_feature) 的矢量
X = face.reshape((-1, 1))
k_means = cluster.KMeans(n_clusters=5, n_init=1)
k_means.fit(X)
values = k_means.cluster_centers_.squeeze()
labels = k_means.labels_
face_compressed = np.choose(labels, values)
face_compressed.shape = face.shape
plt.imshow(face_compressed)
# 导入科学计算库Scipy并缩写为sp
import scipy as sp
try:
# 创建face对象,设置为灰度
face = sp.face(gray=True)
except AttributeError:
from scipy import misc
face = misc.face(gray=True)
# 将图像转化为形如 (n_sample, n_feature) 的矢量
X = face.reshape((-1, 1))
k_means = cluster.KMeans(n_clusters=5, n_init=1)
k_means.fit(X)
values = k_means.cluster_centers_.squeeze()
labels = k_means.labels_
face_compressed = np.choose(labels, values)
face_compressed.shape = face.shape
plt.imshow(face_compressed)

层次凝聚聚类(Hierarchical Agglomerative Clustering)
层次聚类是
**凝聚(Agglomerative) - ** 自下而上的方法:开始每个采样点都自成一类,然后逐渐迭代合并,使得判别式最小化。当每个聚类包含的采样点很少时,此法尤其适用。但当聚类的总数很大的时候,计算消耗会超过K-means。
**分离(Divisive) - ** 自上而下的方法:开始所有采样点都共属一类,然后逐渐迭代分裂,形成层次。在处理大量聚类的问题时,此方法不仅慢,而且存在统计学意义上的病态。
连通约束聚类
在凝聚聚类中,可以通过连通图(connectivity graph)指定哪些样本属于一类。在Scikit中,图以其邻接矩阵的形式呈现,且通常是稀疏矩阵。在对图像进行聚类的时候,这个方法很有用,比如检索连通区域(有时也叫连通分量)。
%matplotlib inline
import scipy as sp
import matplotlib.pyplot as plt
from sklearn.feature_extraction.image import grid_to_graph
from sklearn.cluster import AgglomerativeClustering
from sklearn.utils.fixes import sp_version
# 生成数据
try:
face = sp.face(gray=True)
except AttributeError:
# face在更新的Scipy版本中位于misc
from scipy import misc
face = misc.face(gray=True)
# 为加快处理速度,将尺寸缩小至10%
face = sp.misc.imresize(face, 0.10) / 255.
import matplotlib.pyplot as plt
from sklearn.feature_extraction.image import grid_to_graph
from sklearn.cluster import AgglomerativeClustering
from sklearn.utils.fixes import sp_version
# 生成数据
try:
face = sp.face(gray=True)
except AttributeError:
# face在更新的Scipy版本中位于misc
from scipy import misc
face = misc.face(gray=True)
# 为加快处理速度,将尺寸缩小至10%
face = sp.misc.imresize(face, 0.10) / 255.
plt.imshow(face)
特征凝聚
已知稀疏可以有助于缓解维数灾难(相比大量的特征,采样点数量不足)。另一个方法是合并相似的特征:特征凝聚。具体实现方法是,在特征的“方向”上进行聚类,换言之即聚类转置过的数据。
%matplotlib inline
import numpy as np
from sklearn import cluster, datasets
import matplotlib.pyplot as plt
digits = datasets.load_digits()
images = digits.images
X = np.reshape(images, (len(images), -1))
connectivity = grid_to_graph(*images[0].shape)
agglo = cluster.FeatureAgglomeration(connectivity=connectivity, n_clusters=32)
agglo.fit(X)
X_reduced = agglo.transform(X)
X_approx = agglo.inverse_transform(X_reduced)
images_approx = np.reshape(X_approx, images.shape)
plt.imshow(image_approx)
digits = datasets.load_digits()
images = digits.images
X = np.reshape(images, (len(images), -1))
connectivity = grid_to_graph(*images[0].shape)
agglo = cluster.FeatureAgglomeration(connectivity=connectivity, n_clusters=32)
agglo.fit(X)
X_reduced = agglo.transform(X)
X_approx = agglo.inverse_transform(X_reduced)
images_approx = np.reshape(X_approx, images.shape)
变换与逆变换方法
有的预测器会提供变换方法,如降低数据集的维数。
分解:从信号到成分与载荷
成分与载荷
设是多变量数据,接下来的问题是如何解析并在不同的采样基准上重构:载荷
和一系列成分
使得
成立。选择成分有不同的判据。
主成分分析(PCA:Principal Component Analysis)
主成分分析选择信号中代表最大方差的几个分量。
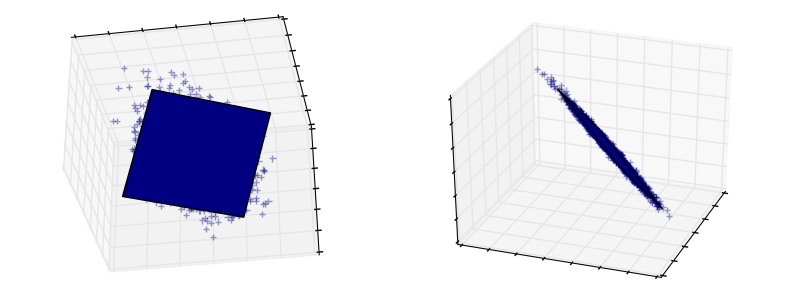
上图中的采样点云在一个方向上非常扁平:三个单变量特征之一甚至几乎可由其他两个计算而来。PCA找的是数据不扁平的那个方向。在变换数据时,PCA可以通过投影到子空间来减少数据的维数。
%matplotlib inline
import numpy as np
# 创建一个变量,只有两个有效维度
x1 = np.random.normal(size=100)
x2 = np.random.normal(size=100)
x3 = x1 + x2
X = np.c_[x1, x2, x3]
from sklearn import decomposition
pca = decomposition.PCA()
pca.fit(X)
# 只有前两个成分是有用的
pca.n_components = 2
X_reduced = pca.fit_transform(X)
X_reduced.shape
# 创建一个变量,只有两个有效维度
x1 = np.random.normal(size=100)
x2 = np.random.normal(size=100)
x3 = x1 + x2
X = np.c_[x1, x2, x3]
from sklearn import decomposition
pca = decomposition.PCA()
pca.fit(X)
# 只有前两个成分是有用的
pca.n_components = 2
X_reduced = pca.fit_transform(X)
X_reduced.shape
X_reduced.shape == (100,2)
from sklearn import decomposition
pca = decomposition.PCA()
pca.fit(X)
独立成分分析(ICA:Independent Component Analysis)
独立成分分析选择一种成分分布,让成分们的载荷带有最多独立信息,并使得还原非高斯(non-Gaussian)信息成为可能。
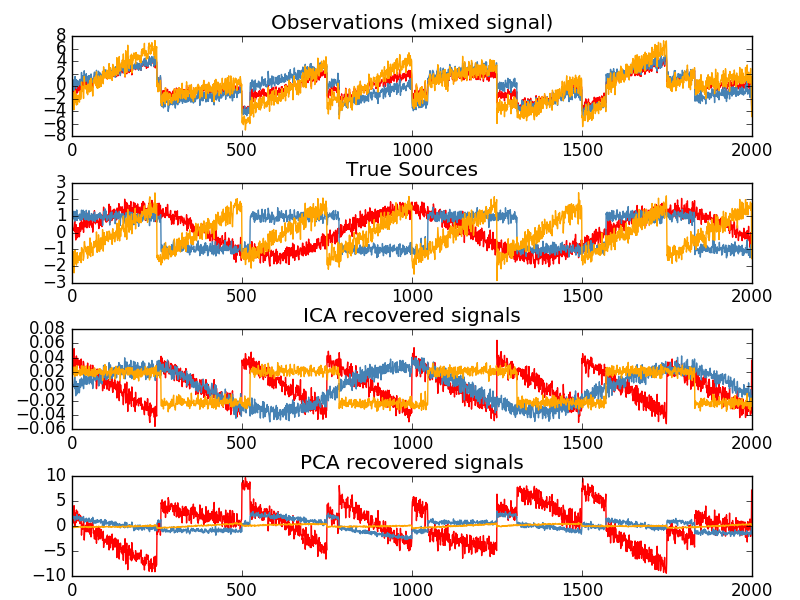
import numpy as np
from sklearn import decomposition
# 生成示例数据
time = np.linspace(0, 10, 2000)
s1 = np.sin(2 * time) # 信号1:正弦波Signal 1 : sinusoidal signal
s2 = np.sign(np.sin(3 * time)) # 信号2:方波
S = np.c_[s1, s2]
S += 0.2 * np.random.normal(size=S.shape) # 添加噪音
S /= S.std(axis=0) # 标准化数据
# 合并数据
A = np.array([[1, 1], [0.5, 2]]) # 合并矩阵
X = np.dot(S, A.T) # 生成采样
# 计算独立成分分析
ica = decomposition.FastICA()
S_ = ica.fit_transform(X) # 获得预测源
A_ = ica.mixing_.T
np.allclose(X, np.dot(S_, A_) + ica.mean_)
# 生成示例数据
time = np.linspace(0, 10, 2000)
s1 = np.sin(2 * time) # 信号1:正弦波Signal 1 : sinusoidal signal
s2 = np.sign(np.sin(3 * time)) # 信号2:方波
S = np.c_[s1, s2]
S += 0.2 * np.random.normal(size=S.shape) # 添加噪音
S /= S.std(axis=0) # 标准化数据
# 合并数据
A = np.array([[1, 1], [0.5, 2]]) # 合并矩阵
X = np.dot(S, A.T) # 生成采样
# 计算独立成分分析
ica = decomposition.FastICA()
S_ = ica.fit_transform(X) # 获得预测源
A_ = ica.mixing_.T
np.allclose(X, np.dot(S_, A_) + ica.mean_)
np.allclose(X, np.dot(S_, A_) + ica.mean_) == True
# 生成示例数据
time = np.linspace(0, 10, 2000)
s1 = np.sin(2 * time) # 信号1:正弦波Signal 1 : sinusoidal signal
s2 = np.sign(np.sin(3 * time)) # 信号2:方波
...
ica = decomposition.FastICA()