BM 算法介绍

各种文本编辑器的 "查找" 功能（Ctrl+F），大多采用 Boyer-Moore 算法。

Boyer-Moore 算法不仅效率高，而且构思巧妙，容易理解。1977 年，德克萨斯大学的 Robert S. Boyer 教授和 J Strother Moore 教授发明了这种算法。

下面我根据书籍 Algorithms on Strings, Trees, and Sequences 的第 2 章 Chapter 2 - Exact Matching: Classical Comparison-Based Methods 来介绍 BM 算法。

好后缀

假设匹配过程中发现 x[i]=a 和 y[i+j] = b 不同，此时当前匹配的信息有：

x[i+1 .. m-1]=y[i+j+1 .. j+m-1]=u

x[i] != y[i+j]

此时我们假设能找到 u 在 x 中的最右出现位置，则可以直接将 x 向右滑动 shift 距离。

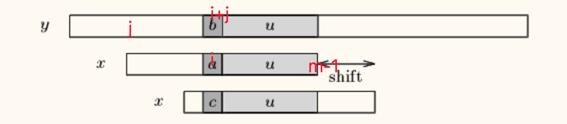
but，如果我们没在 x 中找到 u，则我们尝试去找到 y[i+j+1 .. j+m-1] 的最长后缀 v，同时 v 也是 x 的前缀。

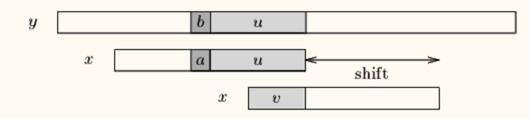
总结下上面两种情况：

• u 可以完整的再次出现在 x 中

• u 的后缀是 x 的前缀

坏字符

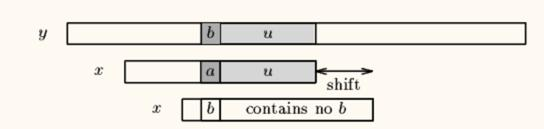
我们找到 y[i+j]=b 在 x 中最右出现的位置，如果没找到直接左对齐 y[i+j+1]：

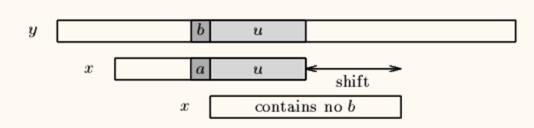
我们可以发现，坏字符的情况中，有可能 shift 是负数。

移动

我们可以根据上面的 好后缀和坏字符分别计算出 shift(好后缀) 和 shift(坏字符) ，我们最后真正移动的 shift 则是 max(shift(好后缀),shift(坏字符))。

算法实现

下面我们来分别计算 shift(好后缀) 和 shift(坏字符)。

先来求 shift(坏字符)，具体算法如下：

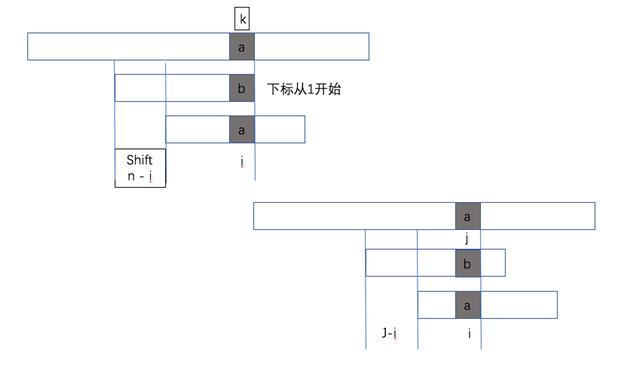
上面图中第一个说明是尾部不匹配的时候，我们查找字符 a 在 pattern 中的位置，假设是 i，则 Pattern shift 的距离是 n-i

第二是是说如果失配发生在 pattern 中第 j 个位置，此时字符 a 在 pattern 中的位置为 i，此时 shift 为 j-i，此时意味着，如果的话，此时我们只能取 shift=1，下面我们来计算

下面我们来看好后缀怎么算计：

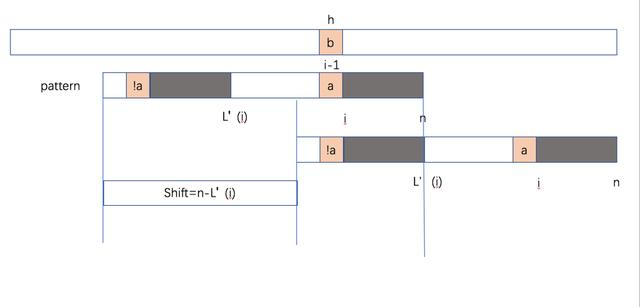
先看上图，我们定义 L(i) 为最大的小于 n 的位置，满足 P[i..n] 是 P[1..L(i)] 的后缀。

接着我们定义 L'(i)，其含义如上图，我们在 L(i) 的基础上，定义 P[i-1] != P[L'(i)-n+i-1]。

举个例子：

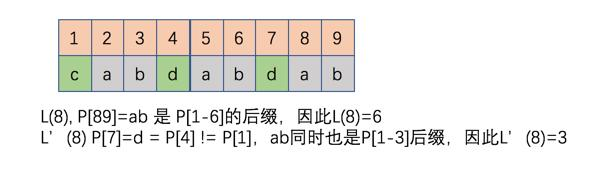
接着我们定义为 P[1..j] 和 P[1..n] 最长公共后缀。

我们来看下定义 P[1..j]，假设存在 i 满足 L‘(i)=j，即 P[i..n] 是同后缀，并且 P[i-1]!=P[j-n+i-1] 也不同，即，此时 L'(i)=j，于是我们就有了下面的算法:

上面算法中我们是假设已经知道了 Nj(P) 了，然后通过 Nj 来计算出 L'(i)，那我们怎么计算 Nj 呢？

计算完 Nj，下面计算 L'：

下面我们看另一种情况，当我们找不到后缀的时候，即 L'(i)=0，我们可以退而求其次，求前缀，看下图：

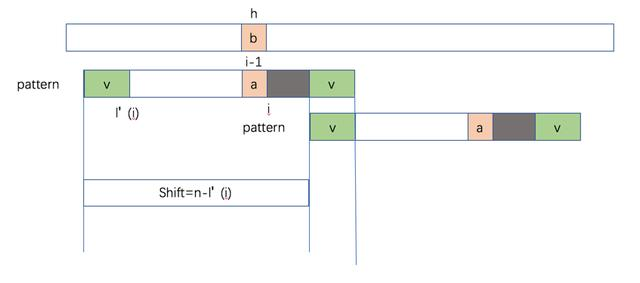
我们定义 l'(i) 是 P[i..n] 的最长后缀同时也是 P[1..n] 的前缀，如果不存在这样子的前缀，则 l'[i] = 0，此时的含义是说，此时 shift=n，为什么移动最大呢？因为我们先去找 Patten 中是否存在 P[i..n]，因为如果要匹配，则 pattern 中必须要存在 P[1..L'(i)]，但是不幸的是没找到，这个时候我们可以直接先 shift i-1，然后在慢慢右移，直到 l'(i)，这个过程如下图：

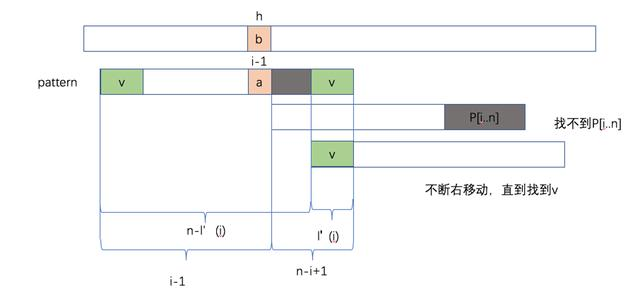
下面就是怎么去计算 l'(i) 了。

我们如果假设 l'(i) 存在，即 l'(i) = j>0，那么此时 Nj(P) = j，并且此时 j 肯定小于等于 |P[i..n]| = n - i + 1，有了这么个洞见以后，我们再来看怎么计算 l'(i).

假设 N[j] == j, j<=n-i+1 => i<=n-j+1，此时 j 越大，i 越小，因此我们就可以这么做了:

代码如下：

现在我们来看下怎么根据 L'(i) 和 l'(i) 来计算 shift 的距离：当 P[i-1] != T[k] 的时候，如果 L'(i) > 0，则移动 n - L'(i)，否则移动 n - l'(i)，此处需要注意一个特殊情况，即 i=n 的时候，我们需要移动 1 位。

代码如下：

好了，现在一切就绪，我们开始整个搜索过程了，完整的搜索代码见 github 地址 。

另外一个完整搜索过程的图示可以看 search examples。

由于头条上Markdown支持不是太好，原文可以看：https://www.zybuluo.com/zhuanxu/note/1035645