给大家看点好玩的，用Python画牛顿分形

今天给大家看点好玩儿的，如何用Python来画牛顿分形。

前排提示：知乎图片压缩严重，非常影响观感，建议点击图片显示原图观看。

分形图是世界上最美妙的图形之一，它结构精细、反常，像是一头怪物难以捉摸。它的每个细节与它的整体如出一辙，在我看来，分形是数学中最优美、吸引人的结构之一。

牛顿分形就是分形的一种，它与解方程的牛顿法(跟优化中的牛顿法是不同的方法)紧密相关，下面讲述如何画出牛顿分形。假如需要求解方程

其中， 的定义域是整个复平面。如何求解这个方程的解呢？我们可以用牛顿法。牛顿法是一种数值解法，我们首先会估算一个“比较好”的初始值 ，然后使用迭代公式

牛顿法可以确保，如果初始猜测值在根附近，那么迭代必然收敛。而且牛顿法是个二阶方法，收敛速度相当的快。下图是迭代一步的示意图

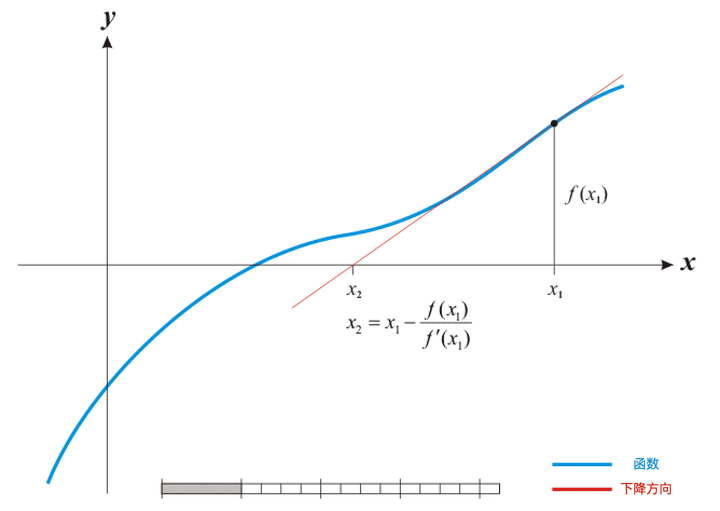
在 处沿着方向 下降，与 轴的交点即为 ，循环往复就能得到方程的根。

学过中学数学的我们都知道， 次方程在复数域上有 个根，那么用牛顿法收敛的根就可能有 个目标。牛顿法收敛到哪个根取决于迭代的起始值。根据最后的收敛结果，我们把所有收敛到同一个根的起始点画上同一种颜色，最终就形成了牛顿分形图。下图中展示的是方程 的情形

图中的三种颜色代表了收敛的三个根，分别为 和 。左上角都是红色的，代表了如果把左上角的点作为牛顿法迭代的初始值，最终会收敛到 ，左下角是绿色，代表这些初始值会收敛到 ，右边是蓝色，代表会收敛到 。神奇的是，中间的三个带状区域，是红绿蓝交错的，而且无限重复自己的细节。

下面看代码。首先是牛顿法解方程

def newton_method(f, df, c, eps, max_iter):
        """f是一个函数,我们要求解f(x)=0 
        df是f的导数
        c是迭代的初始值 
        当两步迭代结果的距离之差小于eps的时候即认为收敛到根
        max_iter是最大迭代次数"""
        for i in range(max_iter):
            c2 = c - f(c) / df(c) # 迭代公式
            if abs(f(c)) > 1e10: # 溢出
                return None, None
            if abs(c2 - c) < eps: # 达到收敛条件
                return c2, i # 返回根和收敛所需的迭代次数
            c = c2

下面就可以用牛顿法画图了，首先我们需要用到下面两个包

import numpy as np
from PIL import Image

然后，我们定义一个取色板函数，根据方程根的次序选取颜色

def color(ind, level):
    """每种颜色用RGB值表示: (R, G, B),
    level是灰度，收敛所用的迭代次数"""
    colors = [(180, 0, 30), (0, 180, 30), (0, 30, 180),
              (0, 190, 180), (180, 0, 175), (180, 255, 0),
              (155, 170, 180), (70, 50, 0),
              (150, 60, 0), (0, 150, 60), (0, 60, 150),
              (60, 150, 0), (60, 0, 150), (150, 0, 60),
              (130, 80, 0), (80, 130, 0), (130, 0, 80),
              (80, 0, 130), (0, 130, 80), (0, 80, 130),
              (110, 100, 0), (100, 110, 0), (0, 110, 100),
              (0, 100, 100), (110, 0, 100), (100, 0, 110),
              (255, 255, 255)]
    if ind < len(colors):
        c = colors[ind]
    else:
        c = (ind % 4 * 4, ind % 8 * 8, ind % 16 * 16)
    if max(c) < 210:
        c0 = c[0] + level
        c1 = c[1] + level
        c2 = c[2] + level
        return (c0, c1, c2)
    else:
        return c

最后，就是我们的画图函数啦。为了少写点参数，我把牛顿法的定义写在`draw`这个函数中，与上面的版本稍有不同。

def draw(f, df, size, name, x_min=-2.0, x_max=2., y_min=-2.0, y_max=2.0, eps=1e-6,
         max_iter=40):
    '''Given function f, its derivative df,
    generate its newton fractal with size, save to image with name
    f是一个函数，我们需要求解方程 f(x) = 0
    df是f的导数
    size是图片大小,单位是像素
    name是保存图像的名字
    x_min, x_max, y_min, y_max定义了迭代初始值的取值范围
    eps是判断迭代停止的条件
    '''
    def newton_method(c):
        "c is a complex number"
        for i in range(max_iter):
            c2 = c - f(c) / df(c)
            if abs(f(c)) > 1e10:
                return None, None
            if abs(c2 - c) < eps:
                return c2, i
            c = c2

        return None, None

    roots = [] # 记录所有根
    img = Image.new("RGB", (size, size)) # 把绘画结果保存为图片
    for x in range(size):
        print("%d in %d" % (x, size))
        for y in range(size): # 嵌套循环，遍历定义域中每个点，求收敛的根
            z_x = x * (x_max - x_min) / (size - 1) + x_min
            z_y = y * (y_max - y_min) / (size - 1) + y_min

            root, n_converge = newton_method(complex(z_x, z_y))
            if root:
                cached_root = False
                for r in roots:
                    if abs(r - root) < 1e-4: # 判断是不是已遇到过此根
                        root = r
                        cached_root = True
                        break
                if not cached_root:
                    roots.append(root)

            if root:
                img.putpixel((x, y), color(roots.index(root), n_converge)) # 上色
    print(roots) # 打印所有根
    img.save(name, "PNG") # 保存图片

好了，有了这几个函数，我们就可以开始实验了。上面的 的图可以用下面几行代码作出

def f(x):
    return x ** 3 - 1
def df(x):
    return 3 * x * x
draw(f, df, 1000, "x^3-1.png")

类似的，我们可以得到其他函数的牛顿分形图。下面是看图时间。

不知道为啥，知乎图片压缩的好厉害，细节丢失严重。。。

注：这次我们只是简要介绍了作牛顿分形图的原理，画的图还是比较原始和丑陋的。要想作出更漂亮的图，还有两方面需要改进，一是根据迭代收敛次数加入shading，二是颜色选取。这两部分也是有一定技巧的，所以改天另开文章再写吧。

最后，题图是 ，来自Wikipedia