1.写在前面
项目中做了个仪表盘效果,需要支持在java中实时更改最大值以及当前值,效果图如下
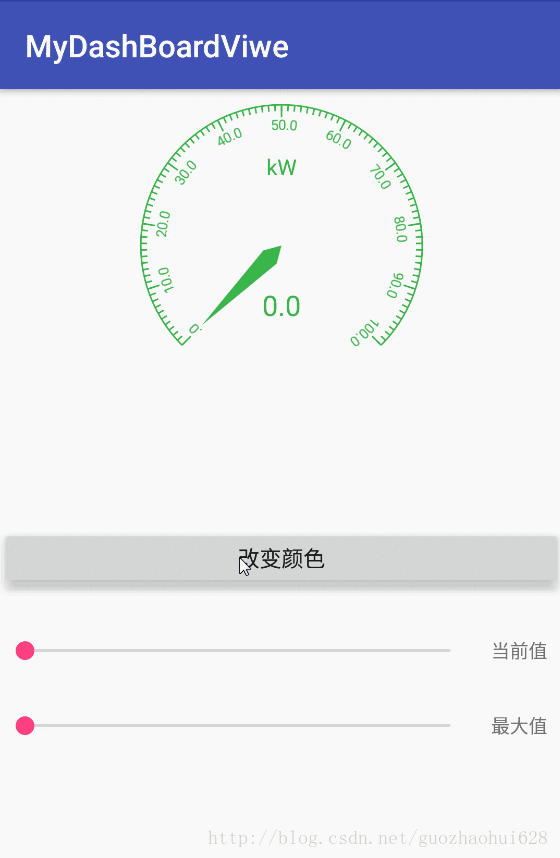
2.实现
首先这个自定义view没有涉及事件分发和动画,纯粹全部都是draw,所以是个练手的好机会。对这个view分析下,可以分为如下几部分
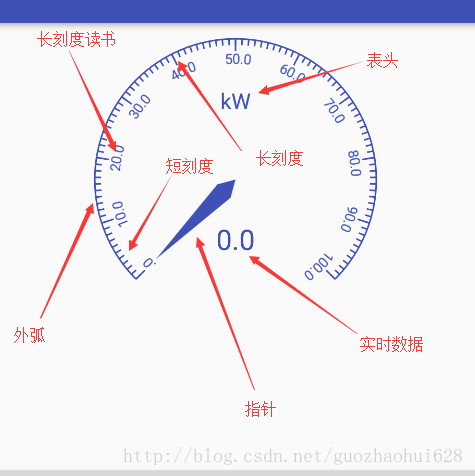
2.1 外弧
我这里方法可能一别人不一样,我首先就移动了画布,将画布的移动到view的中心,所以中心坐标是(0,0),我觉得这样子后面坐标点的坐标好算点。
//整个view的长 宽
private int mWidth,mHeight;
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
mWidth = w;
mHeight = h;
/**
* 圆弧外切矩形的宽度,圆弧的半径即为它的一半
*/
mRectWidth = (float) (Math.min(mWidth,mHeight)*0.9);
}
/**
* 将圆心移到控件中间
*/
canvas.translate(mWidth / 2, mHeight / 2);
上方的Math.min(x,y)*0.9是 正方形类自定义view的常规处理,毕竟这种view的长宽设置时一般都是一样的,但是万一设置的不一样,就取最小的同时在缩小点,留点padding
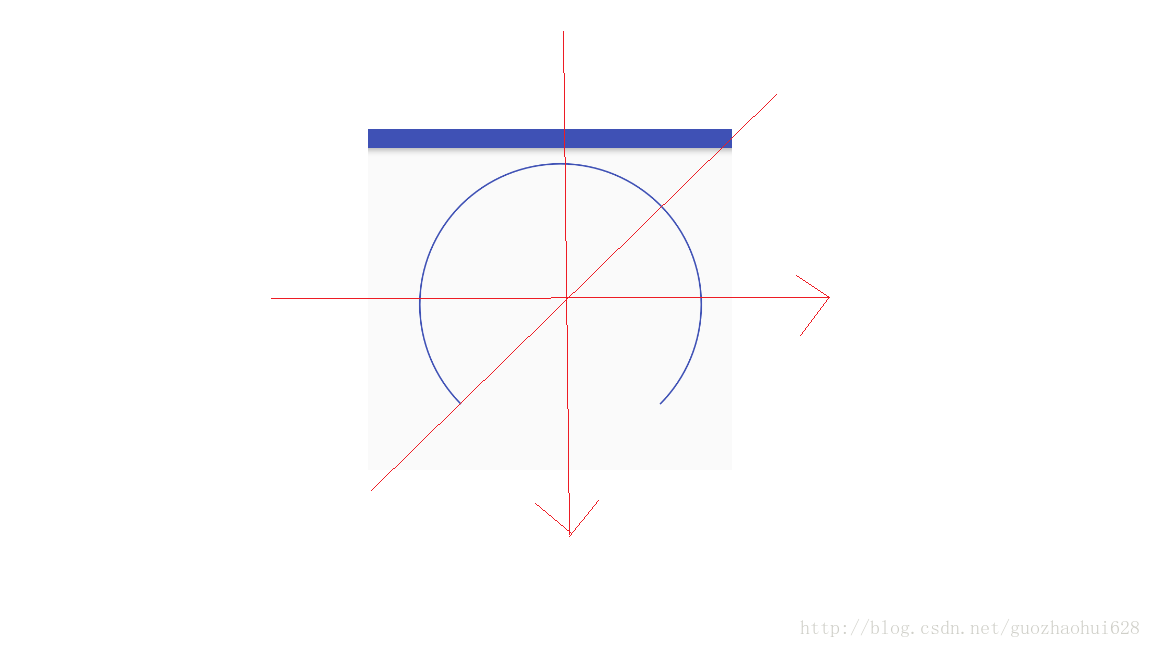
第一步当然画如上图的弧,我为了更明显,红色的坐标系是我加上过去的。这个弧比较容易画,比较明显弧的起始角度是135,弧扫过的角度是270
/**
* 画圆弧
* @param canvas
*/
private void drawArc(Canvas canvas){
mArcPaint.setStyle(Paint.Style.STROKE);
RectF rectFArc = new RectF(-mRectWidth / 2, -mRectWidth / 2, mRectWidth / 2, mRectWidth / 2);
canvas.drawArc(rectFArc,mStartAngle,mSweepAngle,false,mArcPaint);
}
一般来说,画圆弧的第一步是获取圆弧的外切矩形,比如上的rectFArc
2.2 画短刻度
这里为什么是先画短刻度,而不是长刻度,我这里的处理是一共分为十个大份,每个大份分为十个小份,其实长刻度是属于短刻度的,属于包含关系,所以我先讲短刻度画出来,然后长刻度覆盖即可。画短刻度的思路是,先找出短刻度两个点的坐标,然后将两个点这条线画出来,在通过画布旋转。
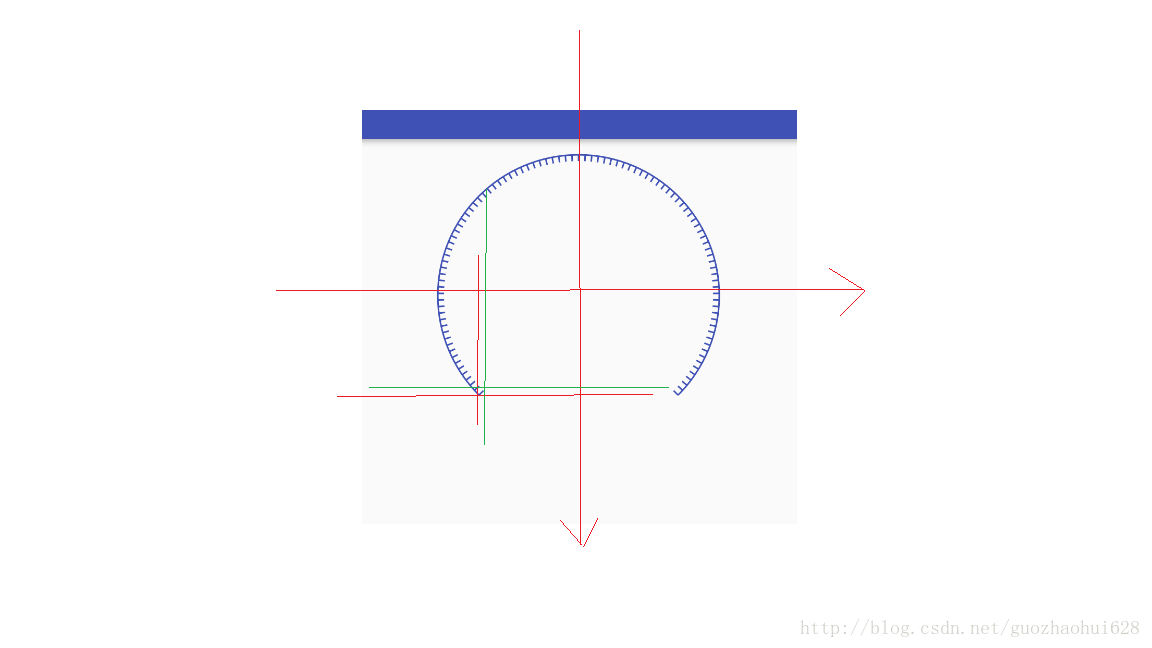
/**
* 画短刻度
* @param canvas
*/
private void drawGraduation2(Canvas canvas){
/**
* 先将画布保存,等下画长度前拿出来,这样 画布相当于是最新的,不然 先画短刻度后 在画长刻度 画布的角度已经变了
*/
canvas.save();
/**
* 将角度135 转成弧度 3pi/4
*/
float startPi = (float) Math.toRadians(mStartAngle);
/**
* 刻度两个点的坐标
*/
float[] point1 = new float[2];
float[] point2 = new float[2];
point1[0] = (float) (Math.cos(startPi)*mRectWidth/2);
point1[1] = (float) (Math.sin(startPi) * mRectWidth / 2);
/**
* 半径减去短刻度的长度,然后算出三角函数
*/
point2[0] = (float) (Math.cos(startPi)*(mRectWidth/2-shortLength));
point2[1] = (float) (Math.sin(startPi) * (mRectWidth / 2 - shortLength));
for(float i=0;i<=270;i+=avgSmallAngle){
canvas.drawLine(point2[0],point2[1],point1[0],point1[1],mArcPaint);
canvas.rotate(avgSmallAngle);
}
}
2.3 画长刻度
长刻度如上一样,只是画布旋转的角度不一样而已,直接看代码即可
/**
* 画长刻度
* @param canvas
*/
private void drawGraduation(Canvas canvas){
canvas.restore();
/**
* 再次保存 为了以后的画布而言,拿出来时 还是最初的
*/
canvas.save();
/**
* 将角度135 转成弧度 3pi/4
*/
float startPi = (float) Math.toRadians(mStartAngle);
/**
* 刻度两个点的坐标
*/
float[] point1 = new float[2];
float[] point2 = new float[2];
point1[0] = (float) (Math.cos(startPi)*mRectWidth/2);
point1[1] = (float) (Math.sin(startPi) * mRectWidth / 2);
point2[0] = (float) (Math.cos(startPi)*(mRectWidth/2-longLength));
point2[1] = (float) (Math.sin(startPi) * (mRectWidth / 2 - longLength));
for(float i=0;i<=270;i+=avgLargeAngle){
canvas.drawLine(point2[0],point2[1],point1[0],point1[1],mArcPaint);
canvas.rotate(avgLargeAngle);
}
}

2.4 画长刻度读数
我们在画长刻度时,首先要获取长刻度的内容,这里代码比较简单,只是我在这里将数据处理了下,所有的数都保留一位有效数字,这样如果最大值是小数时,也可以支持,免得画出来很难看
/**
* 长刻度文本内容数组
*/
private String[] textContent = null;
/**
* 获取长刻度 文字内容
*/
private void getTextContent(){
mMax = getmMax();
textContent = new String[largeSection + 1];
for(int i=0;i<textContent.length;i++){
float avgF = (mMax-mMin)/largeSection;
float result = avgF*i;
Log.d(TAG,"------result------ "+result);
/**
* 对值进行处理,保留一位小数
*/
String lastResutl = new DecimalFormat("#.0").format(result);
/**
* 注意和上面的区别,上面的是 所有的值 始终保留一位小数,下面是 如果是整数则不保留,如果不是整数,则保留一位小数
*/
//String lastResutl = new DecimalFormat("#.0").format(result);
textContent[i] = lastResutl;
}
}
这读数都是随着圆弧画出来的,所以这里使用的方法是drawTextOnPath,其中需要一个path对象,我们需要做的就是给path添加一个圆弧Arc,这里我们需要画11个数据,同时圆弧也要画11次,只不过圆弧每次起点不一样,同时这里我对角度处理了下,等下可以对比下

/**
* 画长刻度 文字
* @param canvas
*/
private void drawText(Canvas canvas){
canvas.restore();
canvas.save();
inArcRect = new RectF(-mRectWidth / 2+longLength+longLength,-mRectWidth / 2+longLength+longLength,mRectWidth / 2-longLength-longLength,mRectWidth / 2-longLength-longLength);
mInPath = new Path();
textRect = new Rect();
mArcPaint.setTextAlign(Paint.Align.LEFT);
mArcPaint.setTextSize(sp2px(9));
mArcPaint.setStyle(Paint.Style.FILL);
for(int i=0;i<textContent.length;i++){
mArcPaint.getTextBounds(textContent[i],0,textContent[i].length(),textRect);
/**
* 处理角度 这里暂时把文字的宽度当作弧长,然后通过弧长算出对应的角度,
* 弧长公式 l(弧长) = n(圆心角) × 派 × r(半径) / 180
* 所以反推出 n = l*180/派×r
*/
int θ = (int) ((textRect.width()/2*180)/(Math.PI*mRectWidth / 2-longLength-longLength));
mInPath.reset();
mInPath.addArc(inArcRect, mStartAngle + i * (mSweepAngle / largeSection)-θ, mSweepAngle);
canvas.drawTextOnPath(textContent[i],mInPath,0,0,mArcPaint);
}
}
不处理是这样的

处理的方法代码中写的很详细了,就是将文字的长度近似于弧长,然后反推弧长公式算出角度,再改变起始角度即可,上面 0 前面那个 . 我已经处理了,写博客时没发现。
2.5 画表头
画表头比较简单,一般来说这种只需设置一次的,设置到xml中比较方便。所以在xml自定义一个表头属性即可。然后在构造函数中获取表头内容,如果为空则不画,不为空 则画出来,画文字这里因为画布在中心的原因比较简单,x坐标为0,y坐标取半径的一般既可,比较简单直接上代码了
/**
* 画表头,如果表头不存在即不画
* @param canvas
*/
private void drawHeadText(Canvas canvas){
if(!TextUtils.isEmpty(mHeadText)){
canvas.restore();
canvas.save();
mArcPaint.setTextSize(sp2px(14));
mArcPaint.setTextAlign(Paint.Align.CENTER);
//mArcPaint.getTextBounds(mHeadText,0,mHeadText.length(),textRect);
canvas.drawText(mHeadText,0,-mRectWidth/4,mArcPaint);
}
}
2.6 画指针
这里我画指针的思路是先算出指针的角度,然后找出指针的四个点坐标,通过path画出来即可,所以指针的难点是找出四个点的坐标。我这里画了个草图,将指针四个点排下序。
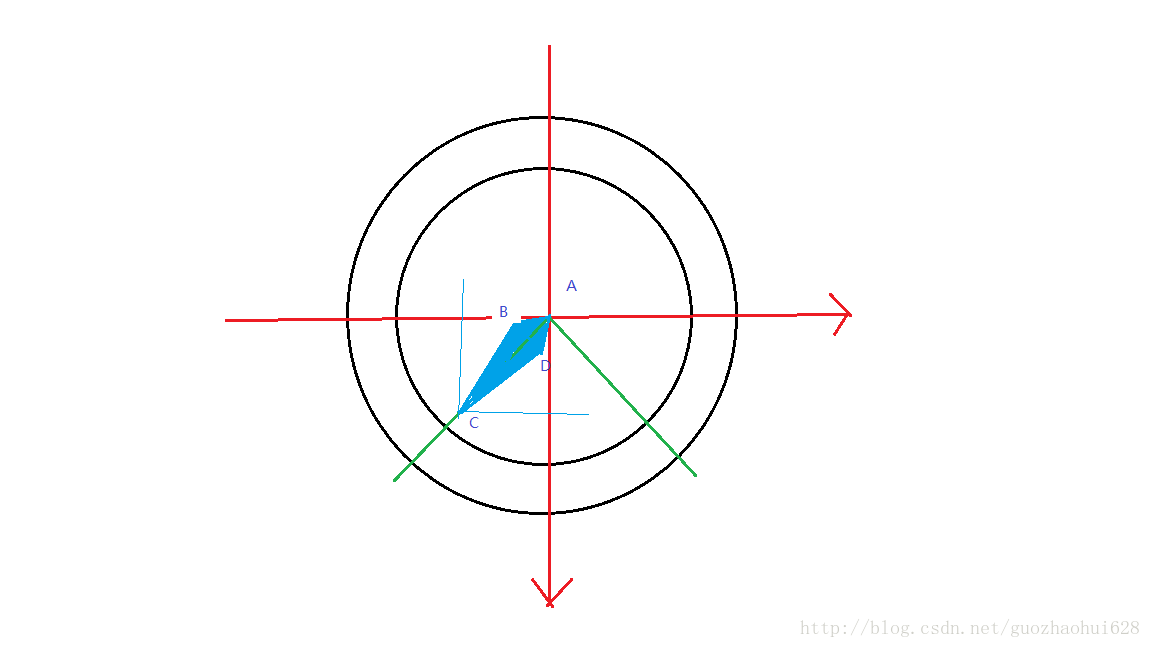
/**
* 画指针,因为这里并不是将 指针画出来 然后算出角度 让它旋转,这里是直接算出角度 然后画出来,所以我们画指针 首先就是算出指针角度
*/
private void drawPointer(Canvas canvas){
canvas.restore();
canvas.save();
float [] pointC = new float[2];
float[] pointB = new float[2];
float[] pointD = new float[2];
mArcPaint.setStyle(Paint.Style.FILL);
/**
* 算出指针的弧度
*/
float angle = (float) Math.toRadians((mCurrentValue/mMax)*mSweepAngle+mStartAngle);
Log.d(TAG, " ------------angle----------- " + angle);
/**
* 指针的半径
*/
float pointerRadius = mRectWidth/2-longLength-longLength-6;
mInPath.reset();
float d = 36;
/**
* C点坐标 指针最末点的位置坐标(远离圆心)
*/
pointC[0] = (float) (Math.cos(angle)*pointerRadius);
pointC[1] = (float) (Math.sin(angle) * pointerRadius);
/**
* B点坐标
*/
pointB[0] = (float) (Math.cos(angle+Math.toRadians(30))*d);
pointB[1] = (float) (Math.sin(angle + Math.toRadians(30)) * d);
/**
* D点坐标
*/
pointD[0] = (float) (Math.cos(angle - Math.toRadians(30)) * d);
pointD[1] = (float) (Math.sin(angle - Math.toRadians(30)) * d);
mInPath.lineTo(pointB[0], pointB[1]);
mInPath.lineTo(pointC[0], pointC[1]);
mInPath.lineTo(pointD[0], pointD[1]);
mInPath.close();
canvas.drawPath(mInPath,mArcPaint);
}

实时读数和表头是一样的,就不上图和代码了。 到这里为止,剩下的就没什么事了,测量和写公开方法,让外部调用,这里比较套路,就不上代码了,等下看源码即可。