谷歌面试题 | 最长递增子序列Ⅰ. 首先解决最长的递增序列问题，最朴素的做法是深搜，以每一个数为开头，找位置在它后面的且

专栏 | 九章算法

网址 | www.jiuzhang.com

题目描述

给一列没有经过排序的数，计算最长的递增序列有几个

样例

输入：[1,3,5,4,7]

输出 : 2

说明：可见上升的最长序列有这么两个，[1, 3, 4, 7] 和 [1, 3, 5, 7]

输入：[2,2,2,2,2]

输出： 5

说明：最长的长度为 1 ，有5个情况，每个都是2

解题思路分析

Ⅰ. 首先解决最长的递增序列问题，最朴素的做法是深搜，以每一个数为开头，找位置在它后面的且数值比它大的为下一层，显然会超时，考虑用动态规划去解决问题(也就是最长上升序列（LIS），一个经典的动态规划问题)

Ⅱ. 设dp[i]为以该数结尾，能构成的最长序列的长度。进行连接的时候，对于每个数字num[i]，遍历位置在它之前的数字num[j]，如果比这个数小（num[j]<num[i]），也就是能构成一个序列，这样就能进行状态转移，我们令dp[i]=max(dp[i],dp[j]+1)来保证存储的为最长长度，同时可以记录max(dp[i])

Ⅲ. 考虑完题目的长度优先后，我们考虑数量，也就是说最长长度的序列有几个，这个问题需要我们在处理dp的时候来记录，我们设ans[i]为以第i个数结尾的最长序列的个数，与dp同理，ans初值也都是1

Ⅳ. 状态转移的时候，如果dp更新了，也就是说（dp[j]+1>dp[i]）说明这个长度的序列是新出现的，我们需要将ans[i]设置为ans[j]，因为新序列中，最新的数提供了序列的尾巴，数量是由前面积累的（或者说转移）；举例序列[1 1 3 7]我们易得数字3对应的dp=2,ans=2,因为可以构成两个[1 3]那么我们操作到数字7的时候，发现接在3后面最长，就可以转移ans来作为初始数量

Ⅴ. 而当dp[j]+1==dp[i]的时候，如同样例，操作7的时候，我们最先发现了可以接在5后面，最长序列[1 3 5 7],然后发现可以接在4后面，[1 3 4 7]，长度也是4，这时候就同样需要转移ans，加上去 ans[i]+=ans[j]

Ⅵ. 最后我们需要遍历dp，找到dp[i]=我们记录的最大值的时候，累加我们得到的ans[i]，即为所求结果，时间复杂度是O(n^2)

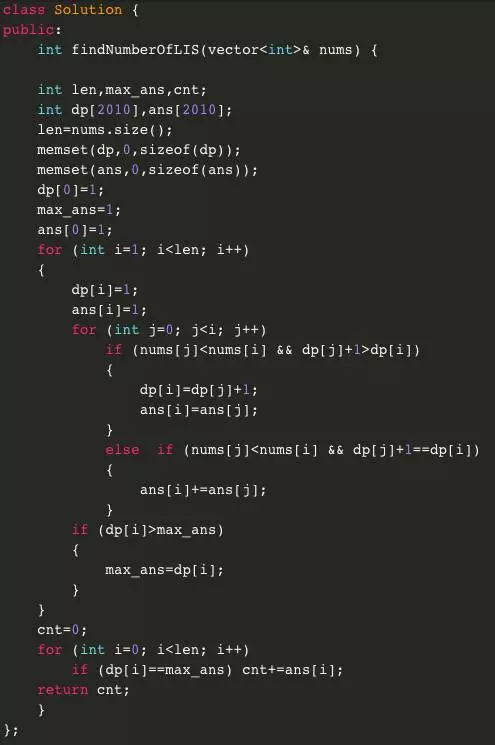
参考程序

Number Of Longest Increasing Subsequence 参考程序

面试官角度分析

本题是一道经典动态规划问题（最长上升子序列）的扩展，难度中等偏简单，给出动态规划算法以及统计次数的方法就可以达到hire

lintcode相关问题

Longest Increasing Subsequence

推荐阅读

欢迎关注我的微信公众号：九章算法（ninechapter）。

精英程序员交流社区，定期发布面试题、面试技巧、求职信息等