左倾堆以及Java实现

左倾堆的定义

左倾堆是一棵二叉树，它的节点除了和二叉树的节点一样具有左右子树指针外，还有两个属性：键值和零距离。

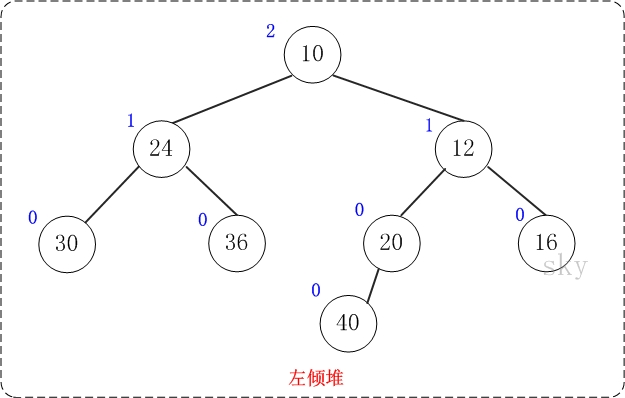
1. 键值的作用是来比较节点的大小，从而对节点进行排序。
2. 零距离(英文名NPL，即Null Path Length)则是从一个节点到一个"最近的不满节点"的路径长度。不满节点是指该该节点的左右孩子至少有有一个为NULL。叶节点的NPL为0，NULL节点的NPL为-1。

基本性质

1. 节点的键值小于或等于它的左右子节点的键值。
2. 节点的左孩子的NPL >= 右孩子的NPL。
3. 节点的NPL = 它的右孩子的NPL + 1。
4. 节点的NPL值等于其右子节点的NPL值 + 1
5. 左倾堆的左右子节点及其下方节点构成的堆也分别都是左倾堆

合并两个左倾堆

1. 如果一个空左倾堆与一个非空左倾堆合并，返回非空左倾堆。
2. 如果两个左倾堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将"较小堆的根节点的右孩子"和"较大堆"进行合并。
3. 如果新堆的右孩子的NPL > 左孩子的NPL，则交换左右孩子。
4. 设置新堆的根节点的NPL = 右子堆NPL + 1

 /**
     * 合并
     *
     * @param x
     * @param y
     * @return
     */
    private LeftistNode<T> merge(LeftistNode<T> x, LeftistNode<T> y) {
        if (x == null)
            return y;
        if (y == null)
            return x;
        //x结点比y结点大
        if (x.key.compareTo(y.key) > 0) {
            LeftistNode<T> temp = y;
            y = x;
            x = temp;
        }
        x.right = merge(x.right, y);
        if (x.left == null || x.left.npl < x.right.npl) {
            LeftistNode<T> tmp = x.right;
            x.right = x.left;
            x.left = tmp;
        }

        if (x.right == null || x.left == null)
            x.npl = 0;
        else
            x.npl = (x.left.npl < x.right.npl) ? x.left.npl + 1 : x.right.npl + 1;
        return x;
    }


    public void merge(LeftistHeap<T> other) {
        merge(mRoot, other.mRoot);
    }

源码