原创作品:cxsmarkchan
个人主页:cxsmarkchan.com
机器学习的样本中通常会存在少量错误标签,这些错误标签会影响到预测的效果。标签平滑采用如下思路解决这个问题:在训练时即假设标签可能存在错误,避免“过分”相信训练样本的标签。当目标函数为交叉熵时,这一思想有非常简单的实现,称为标签平滑(Label Smoothing)。
我们以2类分类问题为例,此时训练样本为(xi,yi),其中yi是样本标签,为0或1。在训练样本中,我们并不能保证所有的样本标签都标注正确,如果某个样本的标注是错误的,那么在训练时,该样本就有可能对训练结果产生负面影响。一个很自然的想法是,如果我们有办法“告诉”模型,样本的标签不一定正确,那么训练出来的模型对于少量的样本错误就会有“免疫力”。
为了达到这个目标,我们的方法是:在每次迭代时,并不直接将(xi,yi)放入训练集,而是设置一个错误率ε,以1-ε的概率将(xi,yi)代入训练,以ε的概率将(xi,1-yi)代入训练。 这样,模型在训练时,既有正确标签输入,又有错误标签输入,可以想象,如此训练出来的模型不会“全力匹配”每一个标签,而只是在一定程度上匹配。这样,如果真的出现错误标签,模型受到的影响就会更小。
那么,这是否意味着我们在每次训练时,都需要对标签进行随机化处理呢?答案是否定的,我们有更好的方法来解决,也就是标签平滑。下面我们介绍标签平滑的具体思路。
当我们采用交叉熵来描述损失函数时,对于每一个样本i,损失函数为:

经过随机化之后,新的标签有1-ε的概率与yi相同,有ε的概率不同(即1-yi)。所以,采用随机化的标签作为训练数据时,损失函数有1-ε的概率与上面的式子相同,有ε的概率为:
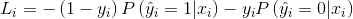
我们把上面两个式子按概率加权平均,就可以得到:
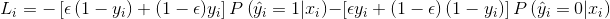
为了简化上面的式子,我们令yi'=ε(1-yi)+(1-ε)yi,可以得到:
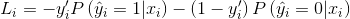
这个式子和原先的交叉熵表达式相比,只有yi被替换成了yi',其他的内容全部都没有变。这实际上等价于:把每个标签yi替换成yi',再进行常规的训练过程。因此,我们并不需要在训练前进行随机化处理,只需要把每个标签替换一下即可。
为什么这个过程被成为标签平滑呢?我们可以从下面的式子看出来:
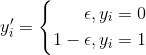
也就是说,当标签为0时,我们并不把0直接放入训练,而是将其替换为一个比较小的数ε. 同样地,如果标签为1,我们也将其替换为较接近的数1-ε。为了方便看出效果,我们可以给出交叉熵模型的表达式:
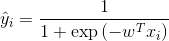
由此可见,在交叉熵模型中,模型输出永远不可能达到0和1,因此模型会不断增大w,使得预测输出尽可能逼近0或1,而这个过程与正则化是矛盾的,或者说,有可能出现过拟合。如果我们把标签0和1分别替换成ε和1-ε,模型的输出在达到这个值之后,就不会继续优化。因此,所谓平滑,指的就是把两个极端值0和1变成两个不那么极端的值。
当然,标签平滑也可以用在多类分类问题中,仍然是假设标签值在一定概率下不变,以一定概率变为其他值。只不过此时有多个其他值,我们可以假设均匀分布,也可以按一定的先验分布处理。如果假设均匀分布,那么标签平滑只需要把所有的标签1变为1-ε,把所有的标签0变为ε/(k-1)即可,其中k是类别的数量。