前言
主成分分析是一种统计学方法,它主要通过降维来简化数据结构,将多个变量转化成少数的几个综合变量,而综合变量能很好地表达原来多个变量的大部分信息,变量之间需要要具备相关性,而经过分析后的变量之间没有相关性。
基本原理
简单从感性角度来了解它的原理就是,比如有两个变量,如下图,看起来它俩的信息量差不多,这时不能忽略某个变量进行降维。
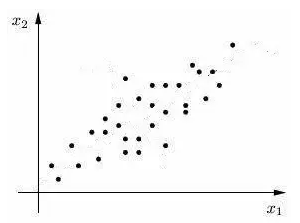
创建一个新的坐标体系PC1和PC2,此时PC1包含的信息量远远大于PC2的,可以忽略掉PC2,于是可以用PC1来表示原来两个维度的信息,达到降维效果。类推到多维情况也是类似如此。
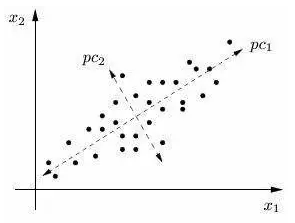
对于有n个变量的m个样本,构成m*n阶的数据矩阵,
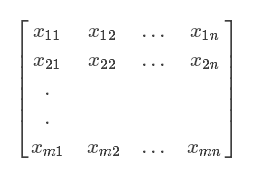
如果变量个数个n较大时,对于我们来说,直接观察这些变量很难看出一些指标,为方便我们观察指标,需要将其降维处理,而且降维后要尽可能多地反应原来包含的信息量。
设有p个主成分,p<n,
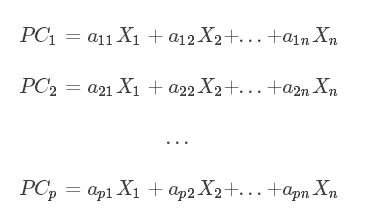
其中PC 之间互相无关。若令
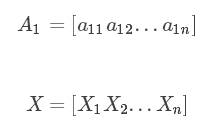
则
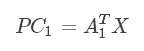
此时向量$A1$称为第一主成分的载荷,计算出来的值为第一主成分的得分。同理其他成分也类似。我们进行主成分分析其实本质就是确定原来变量在p个主成分上的载荷,即$a{ij}$,其中i=1,2,...,p且 j=1,2,...,n。数学上证明$a_{ij}$是相关矩阵的p个较大特征值对应的特征向量。
相关矩阵
相关系数用于描述变量之间相关关系的密切程度,对于p个变量,相关矩阵为,

左上到右下对角线上半部分和下半部分是对称的,$r{ij}$表示两个变量的相关,其中(i,j = 1,2,...,p),且有$r{ij} = r_{ji}$。计算公式如下,
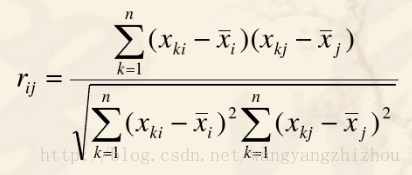
如何确定成分

步骤
- 将原始数据按行排列组成矩阵。
- 将数据进行标准差标准化处理。
- 计算相关系数矩阵。
- 根据相关矩阵计算特征值,并由大到小排列。
- 计算各特征值的特征向量,并且要求
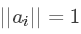
- 计算各主成分的贡献率及累计贡献率,一般选择累计贡献率大于85%的p个主成分。
- 得到p个主成分对应的特征向量,得到各个主成分的载荷。
以下是广告
========广告时间========
鄙人的新书《Tomcat内核设计剖析》已经在京东销售了,有需要的朋友可以到 item.jd.com/12185360.ht… 进行预定。感谢各位朋友。
=========================
欢迎关注:

