管道网络中每条边的最大通过能力(容量)是有限的,实际流量不超过容量。
最大流问题(maximum flow problem),一种组合最优化问题,就是要讨论如何充分利用装置的能力,使得运输的流量最大,以取得最好的效果。求最大流的标号算法最早由福特和福克逊与与1956年提出,20世纪50年Ford、Fulkerson建立的“网络流理论”,是网络应用的重要组成成分。
解决这个问题之前,先看两个相对简单的特例:二分图匹配问题和不相交路径问题。这两个问题本来就代表了各种各样的应用。
和最大流问题思想上一致的是最小切割集的问题。
这两个问题只要解决一个,另一个也会迎刃而解。
这篇文章的基本理念就是:我们希望经由一个网络,以网络的一边为起点,另一边为终点,尽可能多运送某种物质—而对于这些路径有一些附加条件,比如双边匹配,或者以某个单位整数倍进行传输。
下面来说第一个问题,二分图匹配:
我们讨论二分图匹配问题时,通常是指最大化匹配。在这种匹配当中,边的数量应该是追求最大化的。如果情况允许,我们需要寻找的是一种完美匹配。就是里所有的节点都应存在于这个匹配当中。
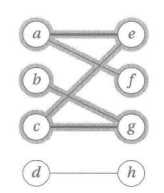
上图是一个二分图的(不是最大化)匹配(粗体的部分),以及从b到f的增广路径(高亮部分)。
然后我们可以开始着手实现解决问题的方法,下面的算法是一种可能的实现方式。参数X和Y都属于可以迭代的对象,表示图G的二分图匹配。它的运行时间可能并不是非常明显,因为执行时边总是被开启和关闭。但是我们可以确定每次迭代都可以增加一对,所以迭代的数量都是O(n),其中n为节点的数量。假设有m条边,那么对于增广路径上的搜索基本上就是对连通分量的遍历也就是O(m)的复杂度。下面是实现的代码:
# 通过增广路径算法来寻找最大双边匹配
from itertools import chain
def match(G, X, Y):
H = tr(G)
S, T, M = set(X), set(Y), set()
while S:
s = S.pop()
Q, P = {s}, {}
while Q:
u = Q.pop()
if u in T:
T.remove(u)
break
forw = (v for v in G[u] if (u, v) not in M)
back = (v for v in H[u] if (v, u) in M)
for v in chain(forw, back):
if v in P:
continue
P[v] = u
Q.add(v)
while u != s:
u, v = P[u], u
if v in G[u]:
M.add((u, v))
else:
M.remove()
return M
def tr(G):
GT = dict()
for u in G:
GT[u] = set()
for u in G:
for v in G[u]:
GT[v].add(u)
return GT
这里的代码,运行时间为O(mn)。
下面说另一个问题,不相交的路径:
增广路径算法也可以用来解决相对于寻找图的匹配来说更加一般化的问题,其中最简单的就是累计边的不相交路径,而不是边的本身的累计。边的不相交路径可以共享节点,但是不能共享边。
最简单的是生命两个特殊的节点s和t,一个是源点,一个是汇点。然后我们要求所有的路径都从s开始。然后从t结束。
如果每个源点和汇点都只属于唯一的路径,如果不用在意拉节点和灌节点之间的配对的话,那么整个题可以被归简为单源点—汇点问题。每次加入一对s、t节点时,就引入了从s到所有源点的边,以及从所有汇点到t的边。路径的数量总是不变的,而重新构造您所要寻找的便只需要重新剪除s和t节点。
对此,我们可以将图分割为互相都独立的小图。然后我们可以加入以下两个规则:
- 对于s和t节点以外,每个节点的入边数量和出边数量必须相等。
- 对任何一条边而言,最多只有一条路径可以占用它。
比如,下图中:
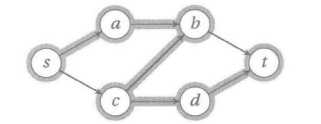
这是一个被发现了一条路径(加粗的边),以及一条增广路径(高亮的边)的s-t网络。
第一次迭代时候,第一条路径被建立了,从s开始,经历c和b,到达t结束。现在任何其他路径都被这条路径阻塞了。但是增广算法可以取消c到b的路径来改进解决方案。
取消操作的工作原理与二分图匹配差不多完全相同,这里不再详细描述。下面是代码实现:
# 使用带标记的遍历来寻找增广路径,并对边不相交的路径计数
from itertools import chain
def paths(G, s, t):
H, M, count = tr(G), set(), 0
while True:
Q, P = dict(s), dict()
while Q:
u = Q.pop()
if u in t:
count += 1
break
forw = (v for v in G[u] if (u, v) not in M)
back = (v for v in H[u] if (v, u) in M)
for v in chain(forw, back):
if v in P:
continue
P[v] = u
Q.add(v)
else:
return count
while u != s:
u, v = P[u], u
if v in G[u]:
M.add((u,v))
else:
M.remove((v, u))
def tr(G):
GT = dict()
for u in G:
GT[u] = set()
for u in G:
for v in G[u]:
GT[v].add(u)
return GT
这段代码的每段迭代都包含了一个相对直白的遍历,运行时间是O(m²)。
下面说下一个问题,最大流问题:
这个问题的通用解决方案当中,一个幼稚的方法是直截了当的对图中的边进行分割。然后我们看一下这个技术,然后我们设置两个规则:
- 除了s和t节点以外,流入节点的流量与流出节点的流量应该相等。
- 对于给定的边,最多只能允许c(e)个单位的流通过
来看一张图:

上图是用伪节点方法来模拟边的容量。
c(e)是边e的容量。
然后继续看下面的图:
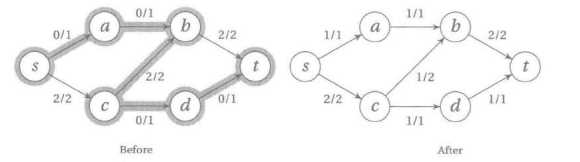
在第一个状态当中,流从s-c-b-t节点依次经过,并且流的值为2.这个流阻塞了其他所有沿着入边的改进。
不过,增广路径包含了反向的边。通过取消从c到b的一个单位的流,我们就可以从c经过d到t增加一个额外的单位,于是我们达到了最大流。
然后看具体的实现代码:
# 通过BFS与标记法来寻找增广路径
from collections import deque
inf = float('inf')
def bfs_aug(G, H, s, t, f):
P, Q, F = {s: None}, deque([s]), {s: inf}
def label(inc):
if v in P or inc <= 0:
return
F[v], P[v] = min(F[u], inc), u
Q.append()
while Q:
u = Q.popleft()
if u == t:
return P,F[t]
for v in G[u]:
label(G[u][v] - f[u, v])
for v in H[u]:
label(f[v, u])
return None, 0
然后是Ford-Fulkerson算法:
# Ford-Fulkerson法(默认使用Edmonds-Karp算法)
from collections import defaultdict
def ford_fulkerson(G, s, t, aug=bfs_aug):
H, f = str(G), defaultdict(int)
while True:
P, c = aug(G, H, s, t, f)
if c == 0:
return f
u = t
while u != s:
u, v = P[v], u
if v in G[u]:
f[u, v] += c
else:
f[v, u] -= c
def tr(G):
GT = dict()
for u in G:
GT[u] = set()
for u in G:
for v in G[u]:
GT[v].add(u)
return GT
下面一个部分,我们说一下最小切割集的问题:
这个问题其实可以用Ford-Fulkerson算法实现。
这里简要证明,我们假设目前所谈论的s-t切割发是这里的唯一的切割方法,然后将该切割集的容量定义其中所通过的流量,这样我们会发现以下三个命题是等价的:
- 我们已经找到了规模为k的流,并且存在一个容量为k的切割集。
- 我们已经找到了最大流。
- 图中而没有增广路径。
这三个命题其实并不难证明,这里不再给出。
下面说最后一个问题,最小成本的流和赋值问题:
解决这个问题的办法,其实是一个贪心算法。我们逐渐建立一个流,每一次迭代中尽可能地增加一些成本。至于这个算法可行性的证明,这里不再给出了。
这里直接给出实现的代码:
# Busacker_Gowen算法,使用Bellman-Ford作为增广算法
def busacker_gowen(G, W, s, t):
def sp_aug(G, H, s, t, f):
D, P, F = {s: 0}, {s: None}, {s:inf, t:0}
def label(inc, cst):
if inc <= 0:
return False
d = D.get(u, inf) + cst
if d >= D.get(u, inf):
return False
D[v], P[v] = d, u
F[v] = min(F[u], inc)
return True
for _ in G:
changed = False
for u in G:
for v in G[u]:
changed |= label(G[u][v] - f[u, v], W[u, v])
for v in H[u]:
changed |= label(f[v, u], -W[v, u])
if not changed:
break
else:
raise ValueError('negative cycle')
return P, F[t]
return ford_fulkerson(G, s, t, sp_aug)
对于算法的运行时间来说,Busacker_Gowen算法的运行时间取决于所选择的最短路径算法。
到这里,这篇文章到这里就要结束了,生活中还是工程中经常会遇到这一章的问题衍生问题。比如棒球淘汰问题、议员选举问题、节假日医生问题、供给与需求的问题和一致性矩阵取整问题等等。
这篇文章主要写的,就是一个核心问题,找到网络中的最大流。基本上所有的解决方案总体思路都是不断迭代改进,不断重复地寻找一条增广路径,让我们的解决方案更优。
写到这里,文章就要结束了。
今天是双十一,作者今天下午参加了一个Google DevFest的活动。也有些收获。作者比较喜欢开源,如果有这个爱好的朋友,大家可以一起交流。
今天的温度,骤然降低,希望大家多穿衣服,注意保暖。
谢谢大家关注。希望大家每天都能进步。