发布人:研究科学家 Maya Gupta,软件工程师 Jan Pfeifer 和 Seungil You
(在 Google 开放源代码博客上交叉发布)
机器学习使用高度灵活的模型来捕获复杂的输入/输出关系,已在许多应用领域取得了巨大进步,其中包括自然语言处理和计算机视觉与建议系统。不过,还未解决的一项挑战是在分析遵守已知全局关系并具有一定语义意义的输入(例如,“如果交通拥堵,行驶一段路程的预估时间将增加,否则将保持不变。”)时存在问题。 DNN 和随机森林一类的柔性模型可能无法学习这些关系,因此,也无法很好地泛化到从与训练模型所用的示例不同的抽样分布中绘制的示例。
今天,我们发布 TensorFlow Lattice,它包含一套易于使用的预构建 TensorFlow 估算器和 TensorFlow 运算符,可以帮助您构建自己的点阵模型。点阵是多维内插式查找表(如需了解详情,请参阅 [1--5]),与几何教材封底近似于正弦函数的查找表类似。为了模型更好地泛化,我们充分利用查找表的结构来满足您指定的 单调关系,这种结构能够通过使用多重输入估计任意柔性关系的方式进行键控。也就是说,查找表值在训练后可以最大程度减少训练示例上的损失,同时,查找表中的邻近值将限制为沿着输入空间的给定方向增大,从而让模型输出在这些方向上增大。重要的是,由于可以内插在查找表值之间,点阵模型非常平滑,预测也有边界限制,这有助于避免测试时出现虚假的大或小预测。
www.youtube.com/watch?v=kaP…
点阵模型如何帮助您
假设您正在设计一个向用户推荐附近咖啡店的系统。您希望模型学习“如果两家咖啡店相同,则选择更近的一家”。我们在下面显示了一个柔性模型(粉色),它可以为东京的用户准确拟合一些训练数据(紫色),这些用户的附近有很多咖啡店。粉色的柔性模型过度拟合了噪声训练示例,并背离了优先选择更近咖啡店的整体趋势。德克萨斯州的咖啡店分布较为分散,如果使用此粉色模型对德州的示例(蓝色)进行排名测试,您会发现模型会表现得非常奇怪,有时甚至选择较远的咖啡店!
相比之下,使用东京的相同示例训练的点阵模型可以被限制为满足此类单调关系,并生成一个单调柔性函数(绿色)。绿线不仅准确拟合了东京训练示例,还很好地泛化到德州示例,从未出现选择距离更远的咖啡店的情况。
一般来说,关于每家咖啡店,您可能有很多输入,例如,咖啡质量和价格等。柔性模型很难捕获以下形式的全局关系:“如果所有其他输入都相同,则选择较近的”,在训练数据稀疏并有噪声的部分特征空间中更是如此。可以捕获先前知识(例如,输入应如何影响预测)的机器学习模型在实际中取得的效果更好,并且更易于调试和解释。
预构建估算器
我们提供了一系列点阵模型架构,例如 TensorFlow 估算器。我们提供的最简单估算器是校准线性模型,它可以学习每个特征(使用一维点阵)的最佳一维变换,然后以线性方式组合所有校准特征。如果训练数据集非常小或者没有复杂的非线性输入交互,这个线性模型将非常有效。另一个估算器是校准点阵模型。这个模型可以使用一个两层单一点阵模型以非线性方式组合校准特征,两层单一点阵模型可以表示您的数据集中复杂的 非线性交互。如果您有 2-10 个特征,校准点阵模型通常是一种比较好的选择,但对于 10 个或更多特征来说,我们认为利用一组校准点阵会取得最佳结果,您可以使用预构建的一组架构来训练这些点阵。与随机森林相比,单调点阵集合可以将准确率提高 0.3-0.5% [4],这些全新的 TensorFlow 点阵估算器可以实现比之前最先进的单调学习模型高 0.1-0.4% 的准确率 [5]。
自行构建模型
您可能想要试验更深层的点阵网络,或者将部分单调函数作为深度神经网络或其他 TensorFlow 架构的一部分开展研究。我们提供以下构建块:TensorFlow 校准器运算符、点阵内插和单调性投影。例如,下图所示为一个 9 层深度点阵网络 [5]。
除了模型选择灵活性和标准的 L1 与 L2 正则化之外,我们还在 TensorFlow Lattice 中提供了全新的正则项:
致谢
开发和开源 TensorFlow Lattice 是一项巨大的团队工作。我们非常感谢所有参与人员:Andrew Cotter、Kevin Canini、David Ding、Mahdi Milani Fard、Yifei Feng、Josh Gordon、Kiril Gorovoy、Clemens Mewald、Taman Narayan、Alexandre Passos、Christine Robson、Serena Wang、Martin Wicke、Jarek Wilkiewicz、Sen Zhao、Tao Zhu
参考文献
[1] Lattice Regression, Eric Garcia, Maya Gupta, Advances in Neural Information Processing Systems (NIPS), 2009
[2] Optimized Regression for Efficient Function Evaluation, Eric Garcia, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
[3] Monotonic Calibrated Interpolated Look-Up Tables, Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
[4] Fast and Flexible Monotonic Functions with Ensembles of Lattices, Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Advances in Neural Information Processing Systems (NIPS), 2016
[5] Deep Lattice Networks and Partial Monotonic Functions, Seungil You, David Ding, Kevin Canini, Jan Pfeifer, Maya R. Gupta, Advances in Neural Information Processing Systems (NIPS), 2017
(在 Google 开放源代码博客上交叉发布)
机器学习使用高度灵活的模型来捕获复杂的输入/输出关系,已在许多应用领域取得了巨大进步,其中包括自然语言处理和计算机视觉与建议系统。不过,还未解决的一项挑战是在分析遵守已知全局关系并具有一定语义意义的输入(例如,“如果交通拥堵,行驶一段路程的预估时间将增加,否则将保持不变。”)时存在问题。 DNN 和随机森林一类的柔性模型可能无法学习这些关系,因此,也无法很好地泛化到从与训练模型所用的示例不同的抽样分布中绘制的示例。
今天,我们发布 TensorFlow Lattice,它包含一套易于使用的预构建 TensorFlow 估算器和 TensorFlow 运算符,可以帮助您构建自己的点阵模型。点阵是多维内插式查找表(如需了解详情,请参阅 [1--5]),与几何教材封底近似于正弦函数的查找表类似。为了模型更好地泛化,我们充分利用查找表的结构来满足您指定的 单调关系,这种结构能够通过使用多重输入估计任意柔性关系的方式进行键控。也就是说,查找表值在训练后可以最大程度减少训练示例上的损失,同时,查找表中的邻近值将限制为沿着输入空间的给定方向增大,从而让模型输出在这些方向上增大。重要的是,由于可以内插在查找表值之间,点阵模型非常平滑,预测也有边界限制,这有助于避免测试时出现虚假的大或小预测。
www.youtube.com/watch?v=kaP…
点阵模型如何帮助您
假设您正在设计一个向用户推荐附近咖啡店的系统。您希望模型学习“如果两家咖啡店相同,则选择更近的一家”。我们在下面显示了一个柔性模型(粉色),它可以为东京的用户准确拟合一些训练数据(紫色),这些用户的附近有很多咖啡店。粉色的柔性模型过度拟合了噪声训练示例,并背离了优先选择更近咖啡店的整体趋势。德克萨斯州的咖啡店分布较为分散,如果使用此粉色模型对德州的示例(蓝色)进行排名测试,您会发现模型会表现得非常奇怪,有时甚至选择较远的咖啡店!
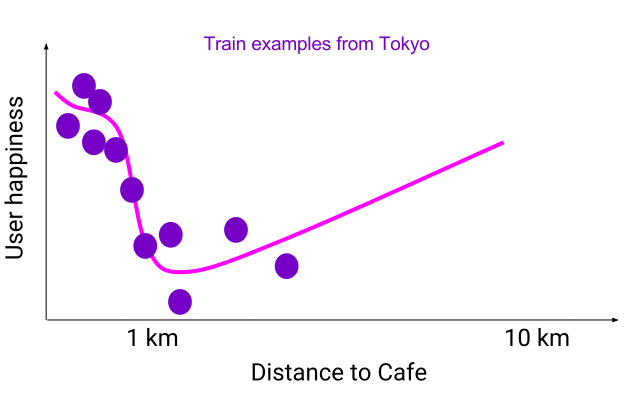 |
| 分割出模型中所有其他输入保持不变,只有距离发生变化的特征空间。在东京的训练示例(紫色)上准确的柔性函数(粉色)预测一家距离为 10 公里的咖啡店优于一家距离为 5 公里的相同咖啡店。如果数据分布发生变化,正如这里德克萨斯州的蓝色示例所示(德州的咖啡店分布较为分散),这个问题在测试时就变得更加明显了。 |
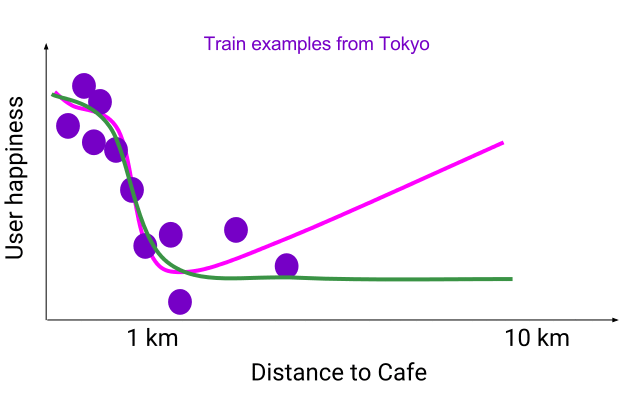 |
| 单调柔性函数(绿色)在训练示例上都是准确的,并且与上一个图中的非单调柔性函数(粉色)相比,可以泛化到德克萨斯州的示例。 |
一般来说,关于每家咖啡店,您可能有很多输入,例如,咖啡质量和价格等。柔性模型很难捕获以下形式的全局关系:“如果所有其他输入都相同,则选择较近的”,在训练数据稀疏并有噪声的部分特征空间中更是如此。可以捕获先前知识(例如,输入应如何影响预测)的机器学习模型在实际中取得的效果更好,并且更易于调试和解释。
预构建估算器
我们提供了一系列点阵模型架构,例如 TensorFlow 估算器。我们提供的最简单估算器是校准线性模型,它可以学习每个特征(使用一维点阵)的最佳一维变换,然后以线性方式组合所有校准特征。如果训练数据集非常小或者没有复杂的非线性输入交互,这个线性模型将非常有效。另一个估算器是校准点阵模型。这个模型可以使用一个两层单一点阵模型以非线性方式组合校准特征,两层单一点阵模型可以表示您的数据集中复杂的 非线性交互。如果您有 2-10 个特征,校准点阵模型通常是一种比较好的选择,但对于 10 个或更多特征来说,我们认为利用一组校准点阵会取得最佳结果,您可以使用预构建的一组架构来训练这些点阵。与随机森林相比,单调点阵集合可以将准确率提高 0.3-0.5% [4],这些全新的 TensorFlow 点阵估算器可以实现比之前最先进的单调学习模型高 0.1-0.4% 的准确率 [5]。
自行构建模型
您可能想要试验更深层的点阵网络,或者将部分单调函数作为深度神经网络或其他 TensorFlow 架构的一部分开展研究。我们提供以下构建块:TensorFlow 校准器运算符、点阵内插和单调性投影。例如,下图所示为一个 9 层深度点阵网络 [5]。
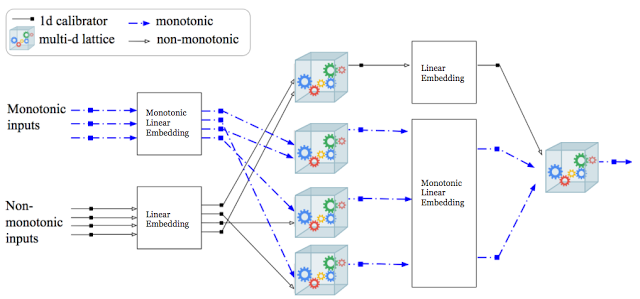 |
| 9 层深度点阵网络架构 [5] 的示例,点阵线性嵌入和集合的交替层,包含校准器层(作为神经网络中整流线性单元的总和)。蓝线对应于单调输入,这些输入逐层保留,从而在整个模型中得到保留。可以使用 TensorFlow Lattice 构建这个架构和其他任意架构,因为每一层都是可以区分的。 |
- 对您的输入选择进行单调性限制 [3],如上文所述。
- 在点阵上进行拉普拉斯正则化 [3],以便让学习函数更扁平。
- 扭曲正则化 [3] 以抑制不必要的非线性特征交互。
致谢
开发和开源 TensorFlow Lattice 是一项巨大的团队工作。我们非常感谢所有参与人员:Andrew Cotter、Kevin Canini、David Ding、Mahdi Milani Fard、Yifei Feng、Josh Gordon、Kiril Gorovoy、Clemens Mewald、Taman Narayan、Alexandre Passos、Christine Robson、Serena Wang、Martin Wicke、Jarek Wilkiewicz、Sen Zhao、Tao Zhu
参考文献
[1] Lattice Regression, Eric Garcia, Maya Gupta, Advances in Neural Information Processing Systems (NIPS), 2009
[2] Optimized Regression for Efficient Function Evaluation, Eric Garcia, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
[3] Monotonic Calibrated Interpolated Look-Up Tables, Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
[4] Fast and Flexible Monotonic Functions with Ensembles of Lattices, Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Advances in Neural Information Processing Systems (NIPS), 2016
[5] Deep Lattice Networks and Partial Monotonic Functions, Seungil You, David Ding, Kevin Canini, Jan Pfeifer, Maya R. Gupta, Advances in Neural Information Processing Systems (NIPS), 2017