代码：曲率滤波代码（所有实验均可重复）
给定一个图像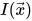
，我们可以把它当作一个三维曲面
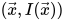。这样，我们就可以利用经典的微分几何工具来处理该三维曲面。假设我们处理后的曲面是
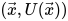，那么我们可以从中提取出处理后的图像
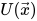，也就是我们处理后的图像。整个过程如标题图片所示。
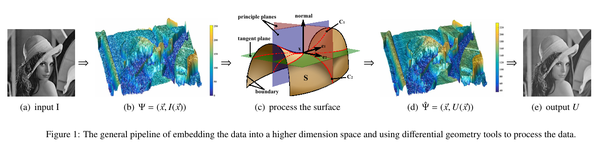
以这种方式进行图像处理的论文非常多，基本的思路都是把图像嵌入三维空间、计算各种曲率（高斯曲率、平均曲率、主曲率等等），然后根据曲率的大小进行各向异性扩散。而且这种扩散方程在数学上是非常完善的，也就是经典的几何流，如下图所示。这么做看起来顺理成章，理论基础也非常扎实，但其实是忽略了一个非常重要的问题：我们的数字图像通常是离散的。
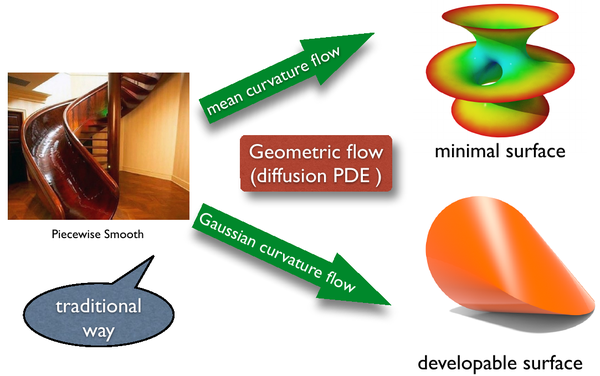
很多读者会问：离散的图像有什么问题？我们还是可以照样计算它的梯度、曲率、方向导数、张量？只不过计算公式被离散化罢了。事实上，真的是公式离散化这么简单吗？离散的数字图像的本质问题在于它的不光滑性。数学上来说，我们的原始图像可能属于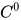
而不属于
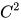。也就是说它本身就是不可导的。对于本身不可导的函数求二阶导数（曲率）的意义是什么呢？
曲率滤波博士论文试图利用图像的离散特性来隐式地优化曲率，即减小曲率而不需要计算曲率。这样就不要求最终的结果二次可导，从而对图像边缘进行更好的保护。一方面，它利用图像的离散特性;
另一方面，它利用连续的微分几何导出一些有用的结论来保证方法的正确性。如何把两者完美地结合起来就非常有挑战性。
接下来就让我们以高斯曲率滤波为例来说明如何利用数据的离散性和微分几何的连续性。一般来说，我们可以把曲面分为可展曲面和不可展曲面两类，如下图所示。
可展曲面可以沿某个基线剪开，然后没有任何拉伸或者扭曲就可以完全平摊在一个平面上（可以展开）。这样的曲面有良好的性质，而且在数学中已经被研究得很透彻。这样的曲面上每一点的高斯曲率为零。我们可以利用这一点来构造曲率滤波，以达到优化曲率的目的。
在连续的微分几何理论中，我们知道高斯曲率处处为零的曲面是可展曲面，而可展曲面只有三类：柱面、锥面和切向可展面。如下图所示，我们可以证明一个定理：
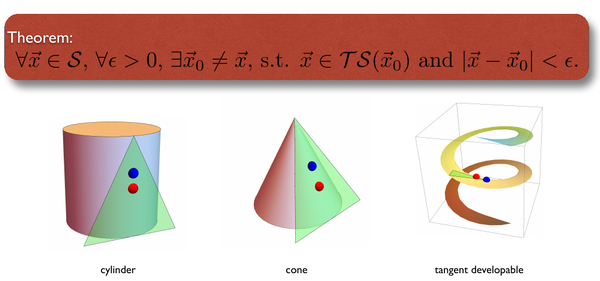该定理说明：对于任何一个可展曲面上的点（如上图红色球所示），它都位于它邻域内某一个点（如上图蓝色球所示）的切面上（如上图绿色三角形所示）。那么，我们怎么样利用这个定理来减小高斯曲率呢？
这就需要利用图像的离散性来构造切面（上图所示的绿色三角形）。在3X3的小窗口内，我们可以枚举所有可能的切面。如下图所示，三个柱面和红色球表示图像的灰度值，绿色三角形表示来自天蓝色三角柱的切面。显然，我们只需要增加或者减小红色球的高度就可以让它位于绿色三角形（切面）上。
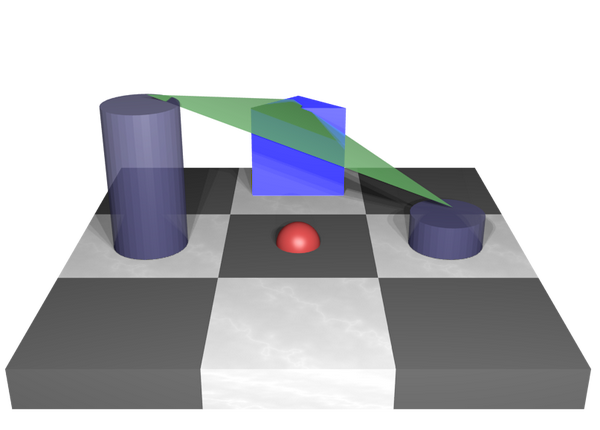利用数据的离散性，我们可以遍历所有可能的切面，然后找到到当前灰度值最小的变化来进行更新，这就完成了一次高斯曲率滤波。我们可以多次重复这一过程，直到收敛。收敛性证明在
曲率滤波博士论文 第六章第一节。
以上过程充分利用了图像的离散特征，也利用了微分几何的连续理论，从而避免了计算曲率和复杂的几何流（数值稳定性，步长，时间离散化等等问题）。更重要的是，这种方式构造的滤波器非常简单，计算速度非常快，比传统的几何流快好几个数量级（优化效果差不多的情况下）。下图是一个例子。左边是原图，中间是经典的高斯曲率几何流，最右边是曲率滤波的结果。视觉上，三者没有太大的差别。但是它们对应的高斯曲率能量分别为246.98, 115.4, 97.15 。传统几何流和曲率滤波的计算时间分别为4246ms 和 18ms。曲率滤波的高效性可见一斑。
简单、高效、通用，是曲率滤波的三个特征。曲率滤波可以单独存在，也可以跟数据拟合项（成像模型）一起工作。而且它可以不要求计算成像模型的梯度。这使得它非常通用，可以求解任意成像模型（black
box）。这是全局算法（global method）做不到的。曲率滤波简单到什么程度呢？下图是Bernstein Filter（优化平均曲率的一种滤波）的算法伪代码（计算太简单了，而且优化效果比state
of the art还要快两个数量级，推导过程见 论文 ）：
当单独使用曲率滤波时，高斯曲率滤波跟其他常见的图像平滑算法有何不同？下表把它和其他经典方法做了简单的对比：
显然，如果输入图像是一个可展曲面，高斯曲率滤波并不会对图像做任何改动。换句话说，高斯曲率滤波保持可展曲面（类似的，平均曲率滤波保持最小曲面）。由于假设的不同和计算方式的不同，这些方法平滑的结果是有些区别的：
简单来说，曲率滤波在平滑和细节保持方面平衡得比较好。这是因为高斯曲率滤波保持分段可展曲面，而其他的只是保持分段线性或者分段常值曲面。后两者是前者的子集，也就意味着曲率滤波的结果产生最少的人工雕琢痕迹（artifacts）。我们为什么要在曲率域做图像处理而不是在梯度域？梯度域不是直接导为Poisson方程吗？有很多高效的解法可以用，而且有很多经典的论文作为基础。我自己也做过梯度域的图像处理，比如 基于梯度分布的图像增强， 基于梯度分布的光学显微镜图像处理。梯度虽然是很好的工具，可以很好地保持sharp edges，但是在实际应用中也有局限性。比如，可不可积就是一个大问题。因为它有多个分量，各个分量之间可能不一致。而曲率是一个标量场，不存在这样的问题。这就是为什么曲率域比梯度域更为理想的原因之一。另外一个原因是曲率是曲面本身的度量，而梯度与坐标系有关。当然，两者也不是完全没有关系。平均曲率就是归一化梯度方向变化的度量。
在曲率滤波提出之前，传统的基于曲率的几何流不能很好地保持sharp edges是因为假设了曲面二次光滑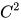。而曲率滤波只要求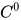，从而能很好地保持梯度（保护边缘，跟梯度等效）。曲率滤波的梯度保持本质上来自于数据的离散性，而光滑性来自于微分几何。这种边缘保持特性可以从上图（与多种滤波算法比较）和下图（除噪实验）中看出。下图最左边为原始图像，中间为噪声图像，右边为高斯曲率滤波后结果。显然，滤波结果在边缘处并不是二次光滑的，而肩膀处的光滑曲面也得到了恢复和保持，没有产生像TV那样的阶梯效应。
曲率滤波博士论文 详细解释了为什么曲率比梯度在理论和实践中更有优势，对很多已知的现象做了理论上的解释和阐述，从本质上开辟了一个优化曲率的新途径（利用数据的离散性和微分几何的连续性）。最近，平均曲率也被证明是一个凸的正则项， Bernstein Filter，这必将促进平均曲率在各种图像处理问题当中的应用。
最后，希望基于曲率的图像处理能够繁荣昌盛！
再贴一次代码链接：曲率滤波代码，希望喜欢的朋友能在github上赏赐一颗星星！
期刊论文链接在 这里。
参考文献：
@ARTICLE{gong:cf, author={Yuanhao Gong and Ivo F. Sbalzarini}, journal={IEEE Transactions on Image Processing}, title={Curvature filters efficiently reduce certain variational energies}, year={2017}, volume={26}, number={4}, pages={1786-1798}, doi={10.1109/TIP.2017.2658954}, ISSN={1057-7149}, month={April},} @phdthesis{gong:phd, title={Spectrally regularized surfaces}, author={Gong, Yuanhao}, year={2015}, school={ETH Zurich, Nr. 22616}, note={http://dx.doi.org/10.3929/ethz-a-010438292}} @INPROCEEDINGS{gong:Bernstein, author={Yuanhao Gong}, booktitle={2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)}, title={Bernstein filter: A new solver for mean curvature regularized models}, year={2016}, pages={1701-1705}, doi={10.1109/ICASSP.2016.7471967}, month={March},} @article{gong:gc, Author = {Yuanhao Gong and Ivo F. Sbalzarini}, Journal = {Intl. Conf. Image Proc. (ICIP)}, Month = {September}, Pages = {534--538}, Title = {Local weighted {G}aussian curvature for image processing}, Year = {2013}}
======================= 点赞过百，为图形学加更 ===========================
以上微分几何理论也完全适用于三角网格处理：
原理是完全一样的，对于三角网格表示的曲面来说，它每一个顶点的邻居也是可以枚举的，如果它是可展曲面，那么它也要满足上述微分几何定理！从而，我们也可以使用相同的方法让三角网格变为可展曲面。曲率滤波博士论文 的附录二（195页）给出了一个简单的例子，如下图所示，经过多次迭代，网格曲面的高斯曲率能量下降了。当然，三角网格的曲率优化更加复杂一点，因为每一个顶点都可以在三维中移动，不像图像中的灰度值只可以上下移动。但是背后的数学原理是一样的。
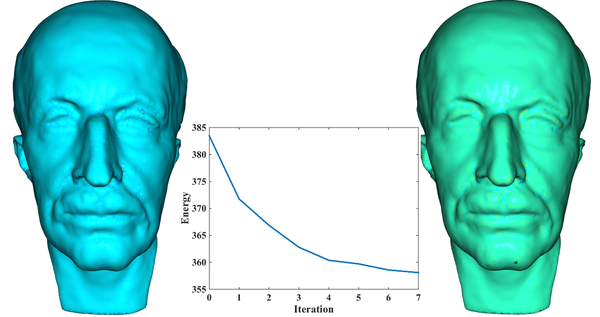
三角网格的高斯曲率滤波的实现是基于 LibIGL（因为当年在ETH读博的时候修过Olga大神的课，所以对这个库比较熟悉，就采用了它）。
让任意曲面变成可展曲面有什么实际意义？因为可展曲面在制造业应用非常广泛，绝大部分人造的东西都是由可展曲面构成的，如下图衣服的设计。最右边给出的就是展开后的可展曲面。显然，这对于其他制造业，比如造船、建筑、服装、汽车、飞机、航天器、智能手机等等，也完全适用。对于制造业，可展曲面的设计比不可展曲面更容易被生产出来。
再来一个建筑设计的例子：
除了对制造业的重要意义意外，可展曲面对于计算机模拟也非常重要。比如需要对如下图右边的复杂曲面进行受热分析。直接在它上面做热传导模拟是挺复杂的（有限元法，粒子方法）。但是如果把它展开，如左图所示，那么在平面上做模拟就简单很多了（不管边界有多复杂）。
这个问题的本质在于计算曲面上任意两点之间的测地线距离。二维曲面本身是一个二维流形，在二维空间计算显然要比在三维空间计算容易得多。不过，外在性质（比如平均曲率、法向量等）就没有得到保持。但是内蕴几何量（比如距离、面积、夹角）会得到保持。
希望这个基于样本离散性和微分几何连续性的想法对做计算机图形学的朋友也有所启迪，从而构造出更好更快的优秀算法来。
