专栏 | 九章算法
网址 | www.jiuzhang.com
题目描述
在二维空间中的一组气球,给出每个气球的横向直径的起始横坐标和结束横坐标,保证起始横坐标小于结束横坐标。
不需要考虑气球的纵坐标,因此横坐标区间可以相互重叠。气球最多有10000个。一支箭可以选定一个横坐标纵向射击。
一个气球的横向直径两端横坐标为xbegin,xend,一支箭射击的横坐标为x,如果有xbegin<=x<=xend,则这支箭可以刺破该气球。没有箭的使用数量限制,并且一支箭可以刺破相应坐标上的所有气球。
求出刺破所有气球所需的最少的箭的数量。
样例
输入: [[10,16], [2,8], [1,6], [7,12]]
输出: 2
说明:
一种方案是在坐标x=6射一支箭(可以刺破气球[2,8]和[1,6]),
在坐标x=11射另一只箭(刺破剩下的两个气球)
解题思路分析
a. 考虑n个区间[s(i), f(i)],i=1,2,……,n,表示n个气球的横向直径的左右端点所表示的区间。如果它们全都互相重叠,那么就可以在它们的相交区间上取一点射箭,这支箭即可刺破所有气球。如果存在互不重叠的区间,那么为了将这些区间的气球刺破,就不得不在这些区间中各射一支箭。
假设区间右端点坐标f(1),f(2),……,f(n),已按从小到大排序,对于这类在一个轴上的区间问题,我们常用的思路是按照左(右)端点排序。考虑第一个区间(右端点坐标f(1)最小的区间),至少要用一支箭将该区间的气球刺破,那么这支箭射在什么位置可以使它刺破尽可能多的气球呢?
答案是区间的右端点坐标。事实上,对于射在任何坐标x<f(1)上的箭能刺破的气球,射在f(1)上一定能刺破,因为f(1)是所有右端点中最小的,在x上能刺破的气球右端点也不会小于f(1)。
这样我们就得到了一个贪心的策略:先按区间右端点f(i)排序,从左往右扫描区间,取出当前右端点坐标最小的区间,在该区间右端点坐标x射出一箭,答案加1,继续往后扫描,去掉所有能被这支箭刺破的气球(s(i)<=x的气球均能被刺破),直到搜索到下一个不能被这只箭刺破的气球,再用同样的方式处理。时间复杂度为排序的时间复杂度O(n*log(n))。
b. Follow up:
本题的输出答案与所有区间中能选出的最多的互不重叠的区间的个数有什么关系?
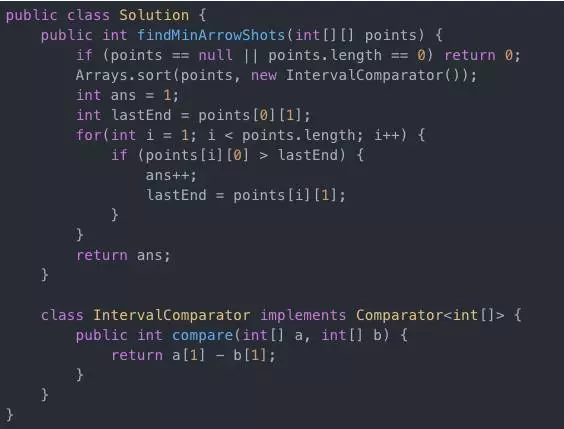
参考程序
面试官角度分析
这题与经典的活动选择问题十分相似,解法是贪心算法,能有清晰的思路并给出解答即可hire。
lintcode相关问题
推荐阅读:
- 网申时, 是否需要 cover letter (求职信) ?
- 2017年最受欢迎的编程语言有哪些?
- HR 揭秘: 10 个挂掉 Offer 的原因
- Google offer 如何谈判?听听 Google recruiter 怎么说!
- 面试遇到做过的题怎么办?
- Snapchat 面经 | LA 总部面试体验
- 面试前如何了解一家IT企业?试试官方技术博客!
- 互联网历史上最有创意的 7 份简历
- 利用 Twitter 找工作 | 如何寻找招聘信息
- Facebook 电面+Onsite面经
欢迎关注我的微信公众号:九章算法(ninechapter)。
精英程序员交流社区,定期发布面试题、面试技巧、求职信息等
