深度学习入门系列，用白话文的方式让你看得懂学的快（第九章、第十章）深度学习入门系列，用白话文的方式让你看得懂学的快，本系

系列文章：

------------------------------------------------------------------------------------

全面连接困何处，卷积网络见解深（深度学习入门系列之九）

原文再续，书接上回。

摘要： 低级动物的眼睛多长在两侧，这样视野广阔，便于避险。而人类的双眼只长在一面，视野有死角，安全难保障，可为什么只有人类“高级”起来，进化成为这个地球的主宰呢？进一步地，是广而肤浅好呢，还是深而专注佳呢？再进一步，这和卷积神经网络又有啥关系？进来瞅瞅呗，历史会告诉你答案。

背景

在前面的文章中，我们介绍了反向传播(Back Propagation，简称BP) 算法，在本质上，BP算法是一种全连接神经网络。BP算法也有很多成功的应用，但只能适用于“浅层”网络，因为“肤浅”，所以也就限制了它的特征表征能力，进而也就局限了它的应用范围。

为什么它难以“深刻”呢？在很大程度上问题就出在它的“全连接”上。难道“全连接”不好吗？它更全面啊，难道全面反而是缺陷？

我们暂时不讨论这个问题，等读者朋友阅读完本专题的系列文章之后，答案自然就会了然于胸。在本章，我们讨论一种应用范围更为广泛的网络——卷积神经网络(Convolutional Neural Network，简称CNN)，它在图像、语音识别等众多任务（比如GoogleNet、微软的ResNet等）上发挥神勇，近几年深度学习大放异彩，CNN可谓是功不可没，拔得头筹。

可为什么CNN能这么生猛呢？答案还得从历史中追寻。著名人类学家费孝通先生曾指出[1]，我们所谓的“当前”，其实包含着从“过去”历史中拔萃出来的投影和时间选择的积累。历史对于我们来说，并不是什么可有可无的点缀之饰物，而是实用的、不可或缺的前行之基础。

下面我们就先聊聊卷积神经网络的历史脉络，希望能从中找到一点启发。在回顾历史之前，我们先尝试思考这样一个“看似题外话而实则不然”的问题：为什么几乎所有低级动物的双眼都是长在头部两侧？

9.1眼在何方？路在何方？

的确，如果你仔细观察，低级动物的双眼大多都长在两侧。从进化论的角度来看，“物竞天择，适者生存”。大自然既然这么安排，自然有它的道理。其中一个解释就是，那些低级动物正是因为这样的“造物安排”，所以能够同时看到上下左右前后等各个方向，从而就不存在视觉盲区。这确实是一种极为安全的配置，有了安全性，它们才能更好地在地球上生存。

可这样的配置又有什么局限呢？相比于低级动物，人的双眼可都是长在面部前方的。这样的配置，肯定不能全方位地观察周遭的一切，这岂不是很糟糕？但事实上是，只有人类进化成为这个地球上最为“高级”的动物。

有人是这样解释的（这个解释的意义可能更多的是来自于意象上的，而非生物学的，所以读者也无需死磕）：低级动物无死角的眼睛配置，虽然能够更全面的关注周围，但副作用却在于，它们没办法把自己的目光集中在某一处，自然也没有办法仔细、长期地观察某个点，于是它们也就不可能进化出深入思考的能力。而人类却因为眼睛的缺陷（接受了视野中的盲区）而能注视前方，从而能给出观察事物的深刻洞察（Insight）。“高级”动物就是这么“练就”出来了。

换句话说，肤浅的全面观察，有时候还不如局部的深入洞察。想一想，那个著名的蝴蝶效应（The Butterfly Effect）是怎么回事，它以“统筹全局”的视角来解释天气的变化：亚马逊雨林一只蝴蝶翅膀偶尔振动，也许两周后就会引起美国得克萨斯州的一场龙卷风。可现实生活中，又有谁真的用“蝴蝶效应”来解决过天气变化问题了呢？我们还不是挥起一把芭蕉扇，利用局部的空气流动，来让自己在酷暑之下获得一丝丝凉意？

可这，和我们今天的主题——卷积神经网络又有什么联系呢？当然有联系，这个联系体现在方法论层面，且听我慢慢道来。

9.2卷积神经网络的历史脉络

我们知道，所谓动物的“高级”特性，体现出来的是行为表象。更深层地，它们也会体现在大脑皮层的进化上。1968年，神经生物学家大卫•休伯尔（David Hunter Hubel）与托斯坦•威泽尔（Torsten N. Wiesel）在研究动物(先后以猫和人类的近亲——猴子为实验对象)视觉信息处理时，有了两个重要而有趣的发现[1]：（1）对于视觉的编码，动物大脑皮层的神经元实际上是存在局部的感受域(receptive field)的，具体说来，它们是局部敏感且具有方向选择性（论文如图9-1所示）。（2）动物大脑皮层是分级、分层处理的。在大脑的初级视觉皮层中存在两种细胞：简单细胞（simple cell）、复杂细胞（complex cell）和超复杂细胞（hyper-complex cell），这些不同类型细胞承担不同抽象层次的视觉感知功能。

（图·9-1休伯尔与威泽尔的经典论文）

正是因为这些重要的生理学发现，使得休伯尔与威泽尔二人获得了1981 年的诺贝尔医学奖。而这个科学发现的意义，并不仅仅局限于生理学，它也间接促成了人工智能在五十年后的突破性发展。

休伯尔等人的研究成果对人工智能启发意义在于，人工神经网络的设计可以不必考虑使用神经元的“全连接”模式。如此一来，就可以大大降低神经网络的复杂性。受此理念的启发，1980年日本学者福岛邦彦（Fukushima）提出了神经认知机(neocognitron，亦译为“新识别机”)模型[3]，这是一个使用无监督学习训练的神经网络模型，其实也就是卷积神经网络的雏形（论文如图9-2所示）。从图9-2中可以看到，neocognitron借鉴了休伯尔等人提出的视觉可视区（visual area）分层和高级区关联等理念。

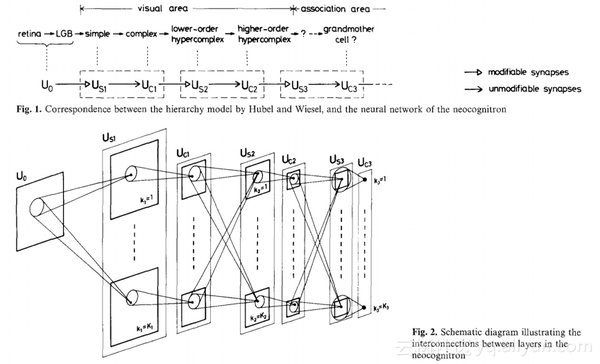
（图9-2 神经认知机的论文）

自此之后，很多计算机科学家先后对“神经认知机”做了深入研究和改进，但其效果却不尽人意。直到1990年，在AT&T贝尔实验室工作的Yann LeCun等人，把有监督的反向传播（BP）算法应用于福岛邦彦等人提出的架构，从而奠定了现代CNN的结构[4]。

相比于传统的图像处理算法，LeCun等人提出的CNN，避免了对图像进行复杂的前期处理（即大量的人工图像特征提取工作），也就是说，CNN能够直接从原始图像出发，经过非常少的预处理，就能从图像中找出视觉规律，进而完成识别分类任务，其实这就是端到端（end-end）的含义。在手写邮政编码的识别问题上，LeCun等人把错误率整到5%左右（论文如图9-3所示）。有了严格的理论基础，并有成功的商业案例应用为之站台，一下子就让卷积神经网络学术界和产业界引爆。

（图9-3 LeCun等人利用卷积神经网络识别手写邮政编码）

LeCun其实也挺“自恋的”，他把自己的研究工作命名为 LeNet，几经版本的更新，最终定格为LeNet 5。在当时，LeNet 架构可谓是风靡一时，但它的核心业务主要用于字符识别任务，比如前文提到的读取邮政编码、数字等。

可问题来了，从1990年到现在，小30年过去了。为什么30年前的技术，到现在突然又以深度学习的面目重新火爆起来了呢？

对于深度学习，吴恩达先生有个形象的比喻：深度学习的过程就犹如发射火箭。火箭想“发飙”，得依靠两法宝：一是发动机，二是燃料。而对深度学习而言，它的发动机就是“大计算”，它的燃料就是“大数据”。

而在30年前，LeCun等人虽然提出了CNN，但其性能严重受限于当时的大环境：没有大规模的训练数据，也没有跟得上的计算能力，这导致了当时CNN网络的训练过于耗时且识别效果有上限。

而与LeCun同在一个实验室的“老冤家”Vapnik（万普尼克），提出并发扬光大了支持向量机 (Support Vector Machine，简称SVM)。这个SVM很了不起，在1998年，就把LeCun等人同类任务的识别错误率一下子降到低至0.8%，远超同期的卷积神经网络。就这样，在SVM的崛起中，神经网络研究沉寂于一个新的低潮！

有人把“Yann LeCun”的中文名称翻译成“严乐春”。的确，“三十年河东，三十年河西”，当“大计算”和“大数据”不再是问题的时候，严乐春用了三十年迎来了自己的又一“春”。当前，严乐春以深度学习大牛的身份出席各大会议，做了一场又一样的主题报告（keynote speech），他用自己的亲身经历，生动地演绎了“形势比人强”。

LeCun 提出的LeNet，在推进深度学习的发展上可谓是功不可没。后期的卷积神经网络也在LeNet 5 基础上做了很多改良，比如2012年Hinton教授采用新的激活函数（ReLU）等。当前主流的卷积神经网络结构如图9-4所示，其精华大致体现在3个核心操作和3个概念。3个核心是指：卷积（Convolution）、池化（Poling）和非线性处理（ReLU）。三概念是指：局部感受域（Local receptive filed）、权值共享（Weight sharing）和亚采样（Subsampling）。

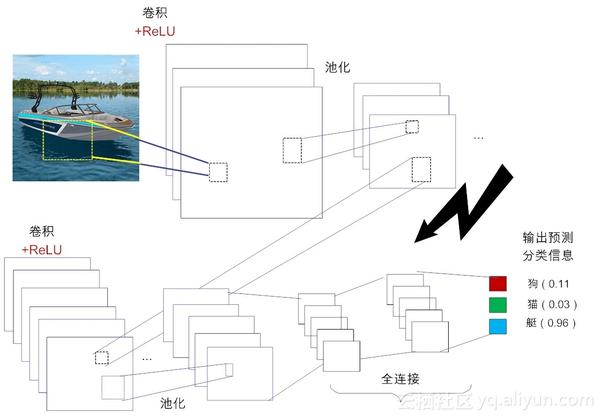
（图9-4 CNN的基本结构）

在后面的章节中，我们会对这些概念一一进行生动形象地介绍，敬请关注。

9.3 小结与思考

在本节中，我们主要回顾了卷积神经网络的发展史，从历史的脉络中，我们可得出一个意象上的结论：深而洞察的专注可能要胜过广而肤浅的观察。这也从方法论上部分解释了“深度学习”的成功所在。

进一步地，请你思考如下问题，人类双眼的布局其实是有缺陷的，因为它带来不安全。李笑来先生认为，人只有放弃了部分的安全感，才能获得进步。为了弥补这方面的缺陷，人们可以通过有效的社交和协作将缺点逆转为优势。

社交进而催生出社群，但社群数量超过150人，人们单纯的社交就显得无能为力了。新锐历史学家尤瓦尔·赫拉利在《人类简史》中表明观点，人类需要通过“讲故事”的方式来完成大规模的协作。你认可这个观点吗？为什么？

留言写下你的感悟，祝你每天都有收获。

参考文献

[1] 费孝通.乡土中国.北京大学出版社.2012年10月

[2] Hubel D H, Wiesel T N. Receptive fields and functional architecture of monkey striate cortex[J]. The Journal of physiology, 1968, 195(1): 215-243.

[3] Fukushima K, Miyake S. Neocognitron: A self-organizing neural network model for a mechanism of visual pattern recognition[M]//Competition and cooperation in neural nets. Springer, Berlin, Heidelberg, 1982: 267-285.

[4] LeCun Y, Boser B E, Denker J S, et al. Handwritten digit recognition with a back-propagation network[C]//Advances in neural information processing systems. 1990: 396-404.

文章作者：张玉宏，著有《品味大数据》一书。审校：我是主题曲哥哥。

---------------------华丽的分割线---------------------

卷地风来忽吹散，积得飘零美如画（深度学习入门系列之十）

摘要： “此情可待成追忆”。可“记忆”到底是什么？如果我告诉你，“记忆”就是一种“卷积”，你可别不信。卷积并不神秘，它就在你我的生活中，它就在深度学习里！这可能是史上最通俗易懂的关于“卷积”介绍文章，不信你就进来瞅瞅呗。

在前面的章节中，我们简要地介绍了卷积神经网络的来龙去脉。接下来我们逐一来解释它之所以成功的几个核心要素。卷积神经网络的名字就来自于其中的卷积操作。因此说到卷积神经网络，它最核心概念可能莫过于“什么是卷积”？

10.1 卷积的数学定义

脱离卷积神经网络这个应用背景，“卷积”其实是一个标准的数学概念。早在3.4节中，我们已经提及到“卷积”的概念：所谓卷积，不过是一个函数和另一个函数在某个维度上的加权“叠加”作用而已[1]。为了更好地理解卷积操作的数学意义，下面我们列举一个具体的案例来加以说明[2]。

假设我们的任务是实时监控一艘宇宙飞船。这艘宇宙飞船带有激光发射器。激光发射器在任意时刻t 都实时输出信号 f(t) ，这里 f(t) 表示飞船在任意时刻 t 所处的位置。通常来说，激光信号中都会夹杂有一定的噪音信号 g(t) 。为了能更加准确地测量飞船的位置，就需要减少噪音的影响，因此我们就需要对获取的距离信号x(t)进行平滑处理。

很显然，对于相邻时间的输出结果，距离当前时间较近的输出，它们对结果的输出影响也较大（分配较大的权值）。反之，距离当前时间越远，它们对当前结果的影响也就越小（分配较小的权值）。因此，加权平均后的飞船位置s(t) 可以用如公式(10.1)表示：

这样的操作就被称为连续域上的卷积操作。这种操作通常也简单记为公式(10.2)：

在公式（10.2）中，通常把函数f称为输入函数， g 称为滤波器或卷积核（kernel），这两个函数的叠加结果称为特征图或特征图谱（feature map）

在理论上，输入函数可以是连续的，因此通过积分可以得到一个连续的卷积。但实际上，目前基本上所有计算机都是数字计算机，这样的计算机是不能处理连续（模拟）信号的。因此需要把连续函数离散化。

一般情况下，我们并不需要记录任意时刻的数据，而是以一定的时间间隔（也即频率）采样即可。这么说是有理论根据的，根据香农采样定理，当采样频率应不小于模拟信号频谱中最高频率的2倍时，可以不失真地恢复模拟信号。对于离散信号，卷积操作可用如公式(10.3)表示：

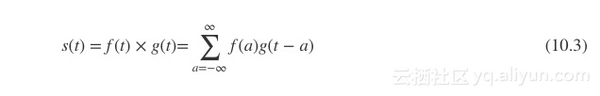
当然，对于离散卷积的定义推广到更高维度的空间上。例如二维的公式可表示为公式（10.4）所示：

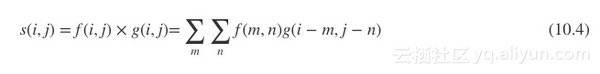
10.2生活中的卷积

卷积的概念好像比较抽象。好在理论来源于现实的归纳和抽象。为了便于理解这个概念，我们可以借助现实生活中案例，来反向演绎说明这个概念。

在前面章节的描述中，我们已经提到，函数（function）就是功能（function），功能就是函数。函数的加权叠加作用，更通俗点讲，就是功能的叠加作用。如果是函数是抽象的，那么功能则是具体的。我们很容易从生活中找到“卷积”影子，从而能更加形象地解释这个概念。在这方面，李德毅院士是高手。

在2015中国计算机大会特邀报告上，笔者有幸聆听了中国人工智能学会理事长李德毅院士的主题报告。在报告中，李院士便提到了卷积的理解问题，非常有意思[3]。

他讲到，什么叫卷积呢？举例来说，在一根铁丝某处不停地弯曲，假设发热函数是f(t) ，散热函数是 g(t) ，此时此刻的温度就是 f(t) 跟g(t)的卷积。在一个特定环境下，发声体的声源函数是f(t) ，该环境下对声源的反射效应函数是 g(t) ，那么这个环境下的接受到声音就是 f(t) 和 g(t) 的卷积。

类似地，记忆其实也是一种卷积的结果。假设认知函数是 f(t) ，它代表对已有事物的理解和消化，随时间流逝而产生的遗忘函数是g(t)，那么人脑中记忆函数 h(t) 就是函数是 f(t) 跟g(t) 的卷积，可用如下公式表示。

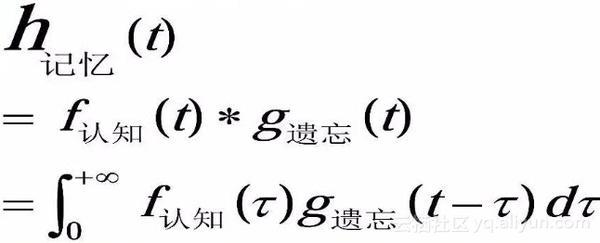
最后，李院士讲到，我们计算机工作者要了解卷积，就要了解卷积神经网络。这个观点和今天讲到的主题很应景，下面我们就言归正“卷”，接着聊卷积神经网络。

10.3在图像处理中的卷积

图像识别是卷积神经网络发威的“圣地”。所以下面我们就以图像处理为例，来说明卷积的作用。

对于如图10-1所示的左侧的图像，正常人很容易判定出，图像中分别是一个数字“8”和一只猫。但是，对于计算机而言，它们看到数字矩阵（每个元素都是0到255之间像素值），至于它们据此能不能判定出是数字“8”和猫，这要依赖于计算机算法，这也是人工智能的研究方向。

（图10-1 计算机“眼中”的图像）

在如图10-1所示的矩阵中，每个元素表示的都是像素的亮度强度。在这里，0表示黑色，255表示白色，数字越小，越接近黑色。在灰度图像中，每个像素值仅表示一种颜色的强度。也就是说，它只有一个通道。而在彩像中，可以有3个通道，即RGB（红，绿，蓝）。在这种情况下，把三个不同通道的像素矩阵堆叠在一起，即可描述彩色图像。

在图像处理中应用卷积操作，主要目的就是从图像中提取特征。卷积可以很方便地通过从输入的一小块数据矩阵（也就是一小块图像）中学到图像的特征，并能保留像素间的空间关系。下面举例说明在二维图像使用卷积过程。

在图10-2中，为了便于读者理解，图像数据矩阵的像素值分别用诸如a-b-c-d这样的字母代替，卷积核是一个2×2的小矩阵。需要注意的是，在其他场合，这个小矩阵，也被称为“滤波器（filter）”或“特征检测器（feature detector）”。

如果把卷积核应用到输入图像的数据矩阵上，依次按照从左到右、从上到下的顺序分别执行卷积运算，就可以得到这个图像的特征图谱（feature map）。在不同的学术论文中，这个术语特征图谱也被称呼为做“卷积特征（convolved feature）”或 “激活图（activation map）”。

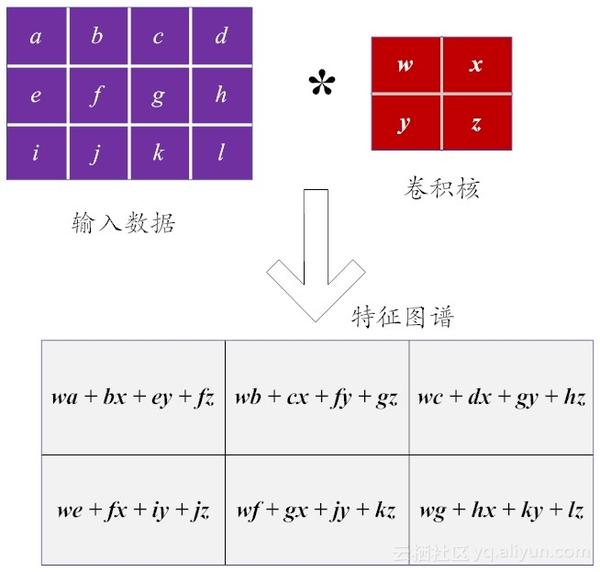
（图10-2 二维图像数据上的卷积操作实例）

从图10-2体现出来的计算可以看到，在本质上，离散卷积就是一个线性运算。因此，这样的卷积操作也被称为线性滤波。这里的“线性”是指，我们用每个像素的邻域的线性组合来代替这个像素。其实，卷积操作还具有平移不变性（shift-invariant）。这个“平移不变性”是指，在图像的每个位置都执行相同的操作。

这个过程好像并不容易理解，下面我们就用更为浅显易懂的动态图来说明这个卷积过程。正如前文所说，每张图片都可视为关于像素值的数字矩阵。对于灰度图像而言，像素值的范围是0 ~255。为了简单起见，我们考虑一个给定5×5 的极简图像，其像素值仅为或0 或 1。类似地，卷积核是一个3×3的极简矩阵，如图10-3所示。

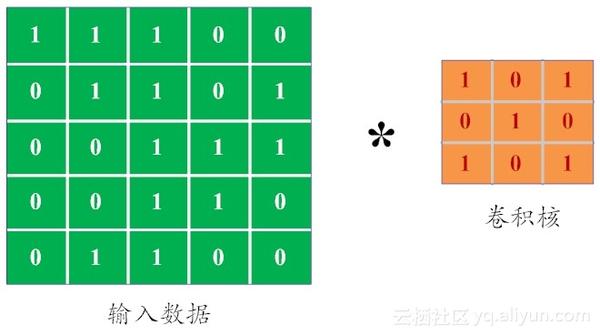
（图10-3 简化版本的图像矩阵核卷积核）

下面我们来卷积计算是怎么完成的。我们用橙色的矩阵在原始图像（绿色所示矩阵）上从左到右、从上到下滑动，每次滑动一个像素，滑动的距离称为“步幅（stride）”。在每个位置上，我们可以计算出两个矩阵间的相应元素乘积，并把点乘结果之和，存储在输出矩阵（粉色所示）中的每一个单元格中，这样就得到了特征图谱（或称为卷积特征）矩阵[5]。

（图10-4 卷积的实现过程）

10.4卷积在图像处理中的应用

到目前为止，我们只是做了一些简单的矩阵运算而已，它的好处体现在哪里，好像还不十分明确。简单来说，这样做的用途在于，将图像相邻子区域的像素值与卷积核执行“卷积”操作，可以获取相邻数据之间的统计关系，从而可挖掘出图像中的某些重要特征。

这样说来，还是非常地抽象，这些特征到底是什么？下面我们还是用几个图像的案例来形象说明这个概念[6]，如图10-5所示。

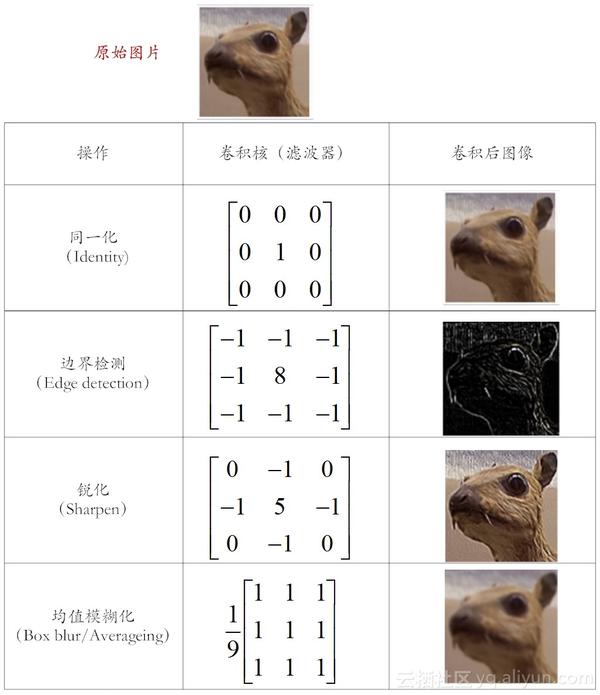
（图10-5 “神奇”的卷积核）

下面我们简单介绍一下常用的“久经考验”的卷积核。

（1）同一化核（Identity）。从图10-5可见，这个滤波器什么也没有做，卷积后得到的图像和原图一样。因为这个核只有中心点的值是1。邻域点的权值都是0，所以对滤波后的取值没有任何影响。

（2）边缘检测核（Edge Detection），也称为高斯-拉普拉斯算子。需要注意的是，这个核矩阵的元素总和为0（即中间元素为8，而周围8个元素之和为-8），所以滤波后的图像会很暗，而只有边缘位置是有亮度的。

（3）图像锐化核（Sharpness Filter）。图像的锐化和边缘检测比较相似。首先找到边缘，然后再把边缘加到原来的图像上面，如此一来，就强化了图像的边缘，使得图像看起来更加锐利。

（4）均值模糊（Box Blur /Averaging）。这个核矩阵的每个元素值都是1，它当前像素和它的四邻域的像素一起取平均，然后再除以9。均值模糊比较简单，但图像处理得不够平滑。因此，还可以采用高斯模糊核（Gaussian Blur），这个核被广泛用在图像降噪上。

事实上，还有很多有意思的卷积核，比如说浮雕核（embossing Filter），它可以给图像营造一种比较艺术化的3D阴影效果，如图10-6所示。浮雕核将中心一边的像素值减去另一边的像素值。这时，卷积出来的像素值可能是负数，我们可以将负数当成阴影，而把正数当成光，然后再对结果图像加上一定数值的偏移即可。