点击上方蓝字“AndroidParks”一起学习、扯淡
文章来源:
http://www.jianshu.com/p/1af5c3655fa3
源码地址:
https://github.com/DeesonWoo/MyBezierCurveView
效果预览:
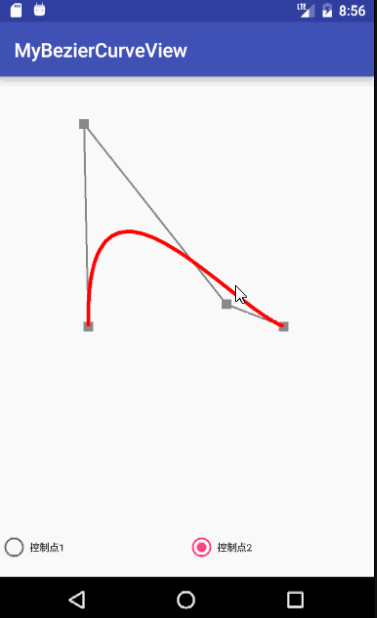
概述
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。
曲线作用
由于用计算机画图大部分时间是操作鼠标来掌握线条的路径,与手绘的感觉和效果有很大的差别。即使是一位精明的画师能轻松绘出各种图形,拿到鼠标想随心所欲的画图也不是一件容易的事。这一点是计算机万万不能代替手工的工作,所以到目前为止人们只能颇感无奈。使用贝塞尔工具画图很大程度上弥补了这一缺憾。贝塞尔曲线是计算机图形图像造型的基本工具,是图形造型运用得最多的基本线条之一。
贝塞尔曲线公式
-
下面的动图来自博客
以下公式中:B(t)为t时间下 点的坐标;P0为起点,Pn为终点,P i为控制点
一阶贝塞尔曲线公式(线性公式)
给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。且其等同于线性插值。
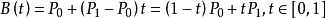
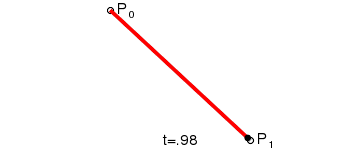
一阶贝塞尔曲线
二阶贝塞尔曲线公式
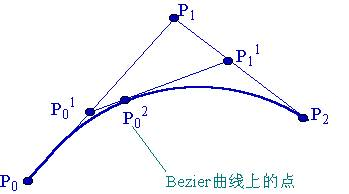
设P0、P02、P 2是一条曲线上顺序三个不同的点。过P0和P2点的两切线交于P 1点,在P02点的切线交P 0P1和P2P 1于P01和P 11,则如下比例成立:
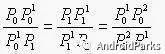
当P0,P2固定,引入参数 t,令上述比值为 t:(1-t),即有:
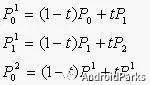
将一式二式代入三式可得:
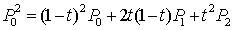
二阶贝塞尔曲线P02可以定义为分别由前两个顶点(P 0,P1)和后两个顶点(P1,P 2)决定的一阶贝塞尔曲线的线性组合。
可得出二阶贝塞尔曲线的公式:
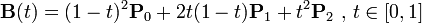
三阶贝塞尔曲线公式
按照二阶的推导原理,以此类推,由四个控制点定义的三阶贝塞尔曲线P03可被定义为分别由(P 0,P1,P2)和(P 1,P2,P3)确定的两条二阶贝塞尔曲线的线性组合:P 03 = (1-t)P0 2 + tP12
可递归代入得出三阶贝塞尔曲线公式:
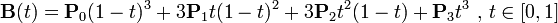
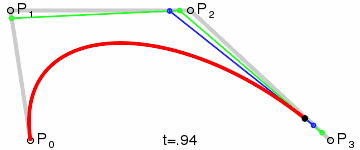
现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝塞尔样条组成的三阶贝塞尔曲线,用来描绘曲线轮廓。
四阶及以上的贝塞尔曲线公式
由(n+1)个控制点 Pi(i=0,1,...,n) 定义的n阶贝塞尔曲线 P0 n 可被定义为分别由前、后 n 个控制点定义的两条 (n-1) 阶贝塞尔曲线 P0n-1 与 P1n-1 的线性组合:
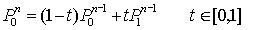
由此得到贝塞尔曲线的递推计算公式(通用公式):
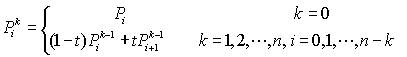
其一般参数公式为:
n 阶贝塞尔曲线可如下推断。给定点P0、P1、…、P n,其贝塞尔曲线即:
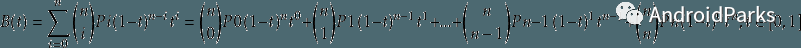
四阶贝塞尔曲线:
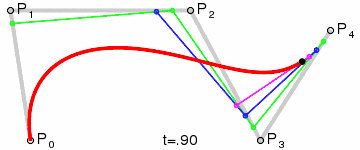
四阶贝塞尔曲线
五阶贝塞尔曲线:
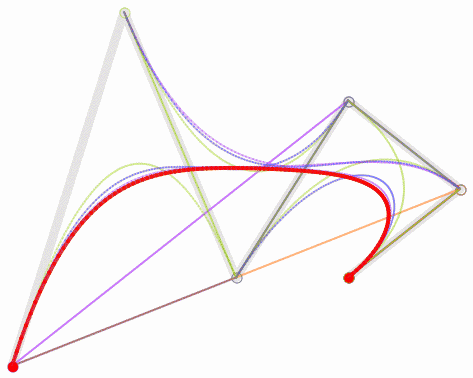
五阶贝塞尔曲线
公式说明
开始于P0并结束于Pn的曲线,即所谓的端点插值法属性。
曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的,贝塞尔曲线是直线的充分必要条件是控制点共线。
曲线的起始点(结束点)相切于贝塞尔多边形的第一节(最后一节)。
一条曲线可在任意点切割成两条或任意多条子曲线,每一条子曲线仍是贝塞尔曲线。
一些看似简单的曲线(如圆)无法以贝塞尔曲线精确的描述,或分段成贝塞尔曲线(虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时,分成四段的贝塞尔曲线,可以小于千分之一的最大半径误差近似于圆)。
位于固定偏移量的曲线(来自给定的贝塞尔曲线),又称作偏移曲线(假平行于原来的曲线,如两条铁轨之间的偏移)无法以贝塞尔曲线精确的形成(某些琐屑实例除外)。无论如何,现存的启发法通常可为实际用途中给出近似值。
Android上实现贝赛尔曲线
在Android实现贝赛尔曲线,要借助android.graphics.Path,其中绘制贝赛尔曲线的方法在Api v1就已经提供了: 这上面是Java层调用的代码,最终调用的是Skia库的一系列方法,Skia是一个C++2D向量图形处理函数库,感兴趣的可以继续深入研究研究。
这上面是Java层调用的代码,最终调用的是Skia库的一系列方法,Skia是一个C++2D向量图形处理函数库,感兴趣的可以继续深入研究研究。
实现二阶贝塞尔曲线
一、首先来看一下可操作的二阶贝塞尔曲线动态图:
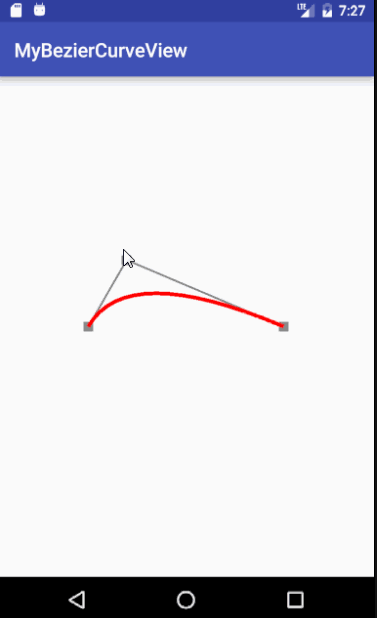
二阶贝塞尔曲线
示例代码查看:自定义 MyBezierCurveQuadratic
二、接着来看,如何用 SurfaceView 实现如下曲线动画效果:
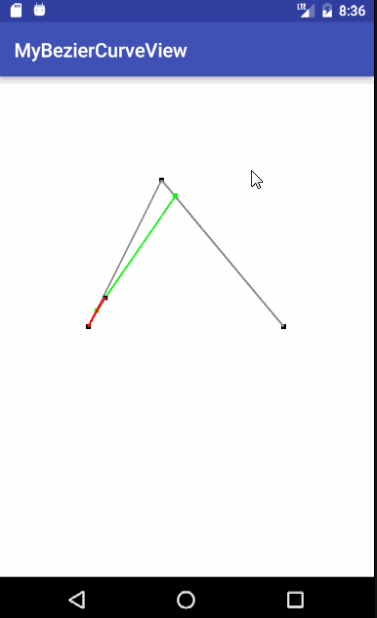
二阶贝塞尔曲线show
这里,最关键的代码是开启子线程绘制二阶贝塞尔曲线,如下: 示例代码查看:自定义 QuadraticBezierShowView 类的完整代码
示例代码查看:自定义 QuadraticBezierShowView 类的完整代码
实现三阶贝塞尔曲线
一、同样的,先看看可操作的三阶贝塞尔曲线:

三阶贝塞尔曲线
示例代码查看:自定义 MyBezierCurveCubic 类的完整代码
二、接着来看,如何用 SurfaceView 实现如下三阶贝塞尔曲线动画效果:
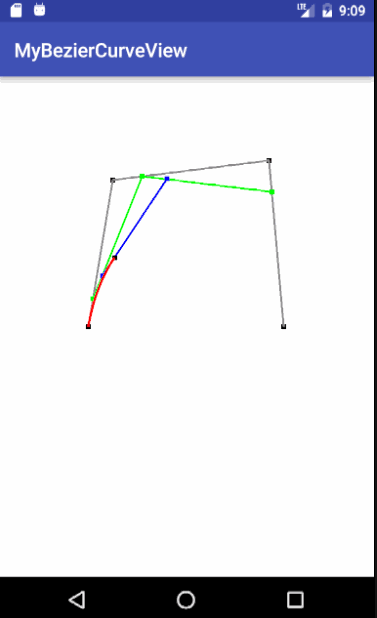
三阶贝塞尔曲线show
示例代码查看:自定义 CubicBezierShowView 类的完整代码

 AndroidParks
关注AndroidParks,和Rance935一起学习、扯淡
AndroidParks
关注AndroidParks,和Rance935一起学习、扯淡