线性表的顺序表示和实现

年前就承诺自己将所了解的数据结构动手实现一遍，但由于时间原因一直拖到了今天才踏出这一步。至于为什么要自己动手去实现基本数据结构，因为我一直很认同尼古拉斯·沃斯提出的观点程序 = 数据结构 + 算法。

如今编程语言越来越多每种语言都有自己的特点，但是我始终认为语言只是表达自己方法的工具而已，而决定你能在这条路上还能走多远的是数据结构，算法，计算机组成原理，计算网络等这些基础理论。

名词解释

线性表定义：

• 是数据结构中最常用且最简单的一种数据结构。简而言之，就是一个线性表是n个数据元素的有限序列。至于每个数据元素的具体含义，在不同情况下各不相同。

线性顺序表定义

• 用一组地址连续的存储单元依次存储线性表的数据元素

基本操作

• Status InitList(SqList *list);
• Status InsertElemIntoList(SqList *list, ElemType elem, int index);
• Status DeleteElemFromList(SqList *list, int index);
• Status ModifyElem(SqList *list, int index, ElemType newElem)
• ElemType GetElemfromList(SqList list, int index);
• int IsLocalElem(SqList list, ElemType elem);
• int GetElemIndex(SqList list, ElemType elem);
• int GetElemIndexFromList(SqList list, ElemType elem);
• Status ClearList(SqList *list);
• Status DestroyList(SqList *list);
• Status TraverseList(SqList list);

在对基本操作的组合就能完成，一些相对比较复杂的操作，比如：两个顺序表的合并等操作。

线性表的顺序表示和实现

线性表的动态分配顺序表存储结构

#define kListInitSize 100       //线性表存储空间的初始化分配量
#define kListIncrement 10       //线性表存储空间的分配增量

typedef int ElemType;

typedef struct {

    ElemType *elem;     //存储空间基地址
    int length;         //当前长度
    int listSize;       //当前分配存储容量，以sizeof(ElemType)为单位
}SqList;

线性表初始化

Status InitList(SqList *list) {

    list->elem = (ElemType *)malloc(kListInitSize * sizeof(ElemType));
    if (!list->elem) {

        return OVERFLOW;
    }
    list->length = 0;
    list->listSize = 0;
    return OK;
}

线性表插入元素

Status InsertElemIntoList(SqList *list, ElemType elem, int index) {

    if (index < 1 || index > list->length+1) {

        return ERROR;
    }
    if (list->length >= list->listSize) {

        ElemType *newBase = (ElemType *)realloc(list->elem, (list->listSize+kListIncrement)*sizeof(ElemType));
        if (!list->elem) {

            return OVERFLOW;
        }
        list->elem = newBase;
        list->listSize += kListIncrement;
    }
    ElemType *insertP = &list->elem[index-1];
    for (ElemType *moveP = &(list->elem[list->length-1]); moveP >= insertP; moveP--) {

        *(moveP+1) = *moveP;
    }
    *insertP = elem;
    list->length ++;
    return OK;
}

当我们一旦因插入元素而空间不足时，就为顺序表在增加一个大小为kListIncrement个数据元素的空间

更具下标删除元素

Status DeleteElemFromList(SqList *list, int index) {

    if (index < 1 || index > list->length) {

        return ERROR;
    }
    for (int i = index; i < list->length; i++) {

        list->elem[i-1] = list->elem[i];
    }
    list->length --;
    return OK;
}

修改元素

Status ModifyElem(SqList *list, int index, ElemType newElem) {

    if (index < 1 || index > list->length) {

        return ERROR;
    } else {

        list->elem[index-1] = newElem;
        return OK;
    }
}

更具下标获取元素

ElemType GetElemfromList(SqList list, int index) {

    if (index < 1 || index > list.length) {

        exit(OVERFLOW);
    }
    return list.elem[index-1];
}

判断是否为线性表中的元素

int IsLocalElem(SqList list, ElemType elem) {

    for (int i = 0; i < list.length; i++) {

        if (list.elem[i] == elem) {

            return 1;
        }
    }
    return 0;
}

获取元素在线性表中的位置

int GetElemIndex(SqList list, ElemType elem) {

    for (int i = 0; i < list.length; i++) {

        if (list.elem[i] == elem) {

            return i+1;
        }
    }
    return 0;
}

清空线性表

Status ClearList(SqList *list) {

    for (int i = 0; i < list->length; i++) {

        list->elem[i] = 0;
    }
    list->length = 0;
    return OK;
}

销毁线性表

Status DestroyList(SqList *list) {

    free(list->elem);
    list->length = 0;
    list->listSize = 0;
    list->elem = NULL;
    return OK;
}

遍历线性表

Status TraverseList(SqList list) {

    for (int i = 0; i < list.length; i++) {

        printf("The %dth elem is %d \n", i+1, list.elem[i]);
    }
    return OK;
}

线性表的特点

根据上面的基本操作，我们不难发现，线性表在进行删除元素和插入元素操作时，都需要移动删除和插入元素之后的元素。换句话说，移动元素的操作为预估算法时间复杂度的基本操作，而移动元素的个数取决于插入或删除的位置。因此从平均时间复杂度来看(假设插入每个位置都是等概率)

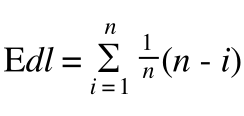
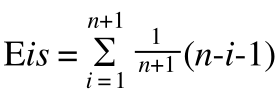
因此在顺序存储结构表的线性表中插入和删除一个元素，平均移动一般的元素，如果表长为n这插入和删除的时间复杂度为O(n)，可以看出顺序存储结构的线性表并不适合做插入和删除

上面基本操作算法中，我们也可以发现，根据下标查找元素和修改元素值等操作的时间复杂度时O(1)

举例

顺序表的合并

在这里我们只讨论listA,listB都是非递减排序，如果没有排序先排序在合并，具体排序算法请参考之前写的一篇排序算法的博客www.jianshu.com/p/7b4be4483…。

Status MergeSqList(SqList listA, SqList listB, SqList *newSqList) {

    int currentIndexA = 0;
    int currentIndexB = 0;
    while (newSqList->length <= listA.length && newSqList->length <= listB.length) {

        if (listA.elem[currentIndexA] > listB.elem[currentIndexB]) {

            InsertElemIntoList(newSqList, listB.elem[currentIndexB], newSqList->length+1);
            currentIndexB++;
        } else {

            InsertElemIntoList(newSqList, listA.elem[currentIndexA], newSqList->length+1);
            currentIndexA++;
        }
    }
    while (listA.length > currentIndexA+1) {

        InsertElemIntoList(newSqList, listA.elem[currentIndexA], newSqList->length+1);
        currentIndexA++;
    }
    while (listB.length > currentIndexB+1) {

        InsertElemIntoList(newSqList, listB.elem[currentIndexB], newSqList->length+1);
        currentIndexB++;
    }
    return OK;
    }

显然在上述算法中基本操作为元素赋值，虽然每次赋值我们都屌用了InsertElemIntoList(SqList *list, ElemType elem, int index)函数，但是有一个特点，我们每次插入都是在表尾进行插入，即不需要西东任何元素。可见两个已经排好序的顺序表合并操作的时间复杂度为O(listA.length + listB.length)

欢迎讨论

Email huliuworld@yahoo.com
Github github.com/LHCoder2016…