0.1 + 0.2 = ? - JS 浮点数失精探究

plusman
2,329 阅读5分钟
原文链接： www.plusman.cn

简述

在 JS 内，0.1 + 0.2 = 0.30000000000000004，而不是想象中的 0.3。

这是一个典型的浮点数失精问题，无论语言，只要采用了 IEEE-754 的浮点数标准，都会出现这个问题，有人还为此专门做了一个名为 0.30000000000000004.com 的网站来罗列各种语言的的输出结果，下面将分析 01 + 0.2 的浮点数运算过程，并讨论浮点数失精的应对方案。

理解下文可能需要以下知识点：

十进制转二进制

计算机内部进行浮点数运算时，是以二进制的形式的进行的，所以我们需要先把十进制转成二进制。

以 4.375 为例子，整数部分依照除二取余法，转换为二进制，例如

4 / 2 =  2..0
2 / 2 =  1..0
4 => 100.

小数部分的转换规则为，对小数部分不停乘 2，顺序对结果取个位值，直到乘积为 1.0，例如

0.375 * 2 = 0.75
0.75 * 2 = 1.5
0.5 * 2 = 1.0
0.375 => 011

前后的计算值合并，则 4.375 的二进制表示为 100.011。

依上规则

// `0.1` 的转换结果为
0.000110011001100110011001100110011(0011) // 接下去为 0011 的循环
// `0.2` 的转换结果为
0.001100110011001100110011001100110011(0011)

二进制浮点数 IEEE-754 表示

IEEE-754 按如下定义表示一个浮点数

浮点数表示
S 为标志位，0 为正数，1为负数
M 代表有效数字，1 <= M < 2
E 为指数位

如果用 64 位存储一个 IEEE-754 标准的浮点数，每位定义如下。

浮点数 64 位存储

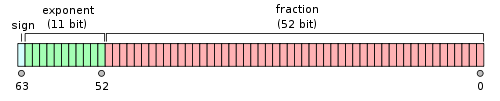
S 存储在 sign 位，占 1 bit。

M 存储在 fraction，由于 fraction 的首位总是 1，所以首位是被隐藏的，相当于有 53 bit 来存储。M 通过小数点左右移动，变更指数位来保证首位为 1。例如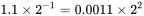

E 存储在 exponent，全名为 Biased-exponent， 采用偏移的方式编码，即没有符号位，指定一个中间值为 0，大于这个值为正数，小于这个值为负数。设 exponent 占用了 L bit，中间值的计算方式为 。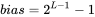

Round to nearest, ties to even 舍入规则

基于上面的规则，我们发现 0.1 的二进制表示，是无限循环小数，但是我们的 M 只有 53 bit 可用。
类似十进制运算的四舍五入，IEEE-754 采用 Round to nearest, ties to even 方式进行舍入，如图。

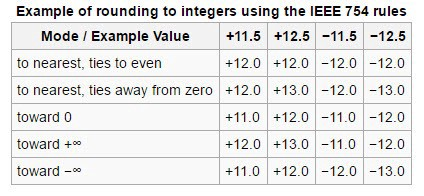
例如二进制小数 0.11100，需要保留 2 位有效数字。
Round to nearest 规则下，有两个可选值 0.11 和 1.00，并且这两个值和原值的差值的绝对值是相同的，这就出现了一个 ties(平局) 的局面，此时触发第二个规则 ties to even，所以最后的舍入结果是 1.00

所以，0.1 最终的浮点数表示为

                      43210 ------ fraction index
1.100...(1100) x 11...11001100
                      11010 ------ 舍入结果

V = 1.100...(1100) x 11...11010 * (2^-4)

同理可得 0.2 为

V = 1.100...(1100) x 11...11010 * (2^-3)

浮点数的加法运算

对阶
对阶的原则是，低阶向高阶对齐，因为小数点右移损失的精度比左移小得多，所以 0.1 对阶后的结果为

V = 0.1100...(1100) x 11...1101 * (2^-3)

符号位+尾数（包含隐藏位）执行加减法
符号位采用双符号判断法， 故正数的符号位为 00。 

00-01100110011001100110011001100110011001100110011001101 -- 0.1
00-11001100110011001100110011001100110011001100110011010 -- 0.2
-------------------------------------------------------------------------------
01-00110011001100110011001100110011001100110011001100111

规格化&舍入
符号位为 01 发生上溢出，执行向右规格化，尾数右移1位，阶码+1，结果为

                                                     210 -- fraction index
01-00110011001100110011001100110011001100110011001100111
00-100110011001100110011001100110011001100110011001100111 -- 尾数右移 1 位
00-10011001100110011001100110011001100110011001100110100 -- 舍入

最后计算结果为
V = 1.0011001100110011001100110011001100110011001100110100 * (2^-2)

可用如下代码，转换为 10 进制

// 小数部分按如下规则累加
0.010011001100110011001100110011001100110011001100110100
  ||__ + 1*2(-2)
  |
  |__0 * (2^-1)

JS 代码示例

'010011001100110011001100110011001100110011001100110100'
  .split('')
  .map(val => +val)
  .reduce((pre, val, index) => {
    return pre + val * (2 ** -(index + 1));
  }, 0);

// 输出 0.30000000000000004

Bingo！证毕。

通过上述演算，我们发现失精发生在舍入部分，换句话说，不能被 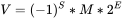浮点数表示 精确表示的浮点数，在运算时会发生失精问题。

失精问题对策

那么我们有哪些方法可以避免呢？

最直接也是生产环境的建议，使用 math.js

JS 实现浮点数精确计算，最基本的原理是：将浮点数拆分成 Number.MIN_SAFE_INTEGER和 至 Number.MAX_SAFE_INTEGER 区间内可被精确表示的数值，然后进行计算和结果汇总。

这里不做深究，读者可自行查阅。

avatar
文章
阅读
粉丝