专栏 | 九章算法
网址 | www.jiuzhang.com
线段树专题
线段树入门问题
给出数列[1 4 2 3],求给定区间的最大值
例:query(0,1) = 4 query(2,3) = 3 query(0,3) = 4
解题思路分析
一道题可不可以用线段树来做,基本是看这道题的操作有没有区间的性质。也就是在一个区间上的操作是否可以转化为两个子区间上的操作。
从这题可以看出
区间(a,b)的最大值和区间(b,c)的最大值中
取较大的就是区间(a,c)的最大值
很明显可以看出这个操作是具有区间的性质。
套路:几种常见的线段树的套路
- 求区间的和,积,最大值,最match小值,gcd等
- 以当前结点的值作为结点处理,比如给出N个数,再给一个数,问比这个数大的有多少个(当然,用树状数组可以很好的处理,但有修改时,线段树就会方便很多)
- 区间加减同一个值,或者区间同时赋一个值(在面试中,通常不会问到,算法竞赛中会经常用到)
构造:一颗线段树的构造就是根据区间的性质的来构造的

区间划分大概就是上述的区间划分。可以看出每次都将区间的长度一分为二,数列长度为n,所以线段树的高度是log(n),这是很多高效操作的基础。
上述的区间存储的只是区间的左右边界。我们可以将区间的最大值加入进来。

区间的第三维就是区间的最大值
加这一维的时候只需要在建完了左右区间之后,根据左右区间的最大值来更新当前区间的最大值即可。
因为每次将区间的长度一分为二,所有创造的节点个数为
n + 1/2 n + 1/4 n + 1/8 n + ...
= (1 + 1/2 + 1/4 + 1/8 + ...) n
= 2n
所以构造线段树的时间复杂度和空间复杂度都为O(n)
代码1:线段树构造代码模板
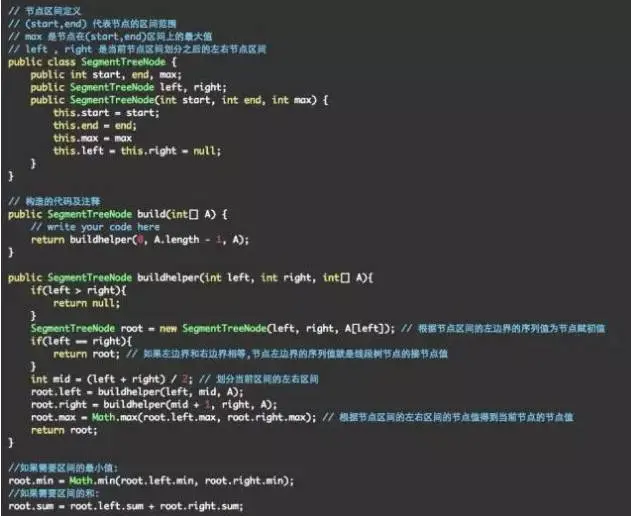
区间查询:构造线段树的目的就是为了更快的查询。
给定一个区间,要求区间中最大的值。
线段树的区间查询操作就是将当前区间分解为较小的子区间,然后由子区间的最大值就可以快速得到需要查询区间的最大值。
query(1,3) = max(query(1,1),query(2,3)) = max(4,3) = 4
上述例子将(1,3)区间分为了(1,1)和(2,3)两个区间,因为(1,1)和(2,3)区间的最大值事先已经记录好了,所以直接拿来用就可以了。
层数:每一层最多查询4个区间
考虑长度为16的序列构造成的线段树,区间(0,15)。查询区间(1,14)。
第一层会查询 (1,7) (8,15)
第二层会查询 (1,3) (4,7) (8,11) (12,14)
第三层会查询 (1,1) (2,3) (12,13) (14,14)
第四层会查询 (1,1) (14,14)
因为是连续的,中间那部分会直接算出来,然后两边的两端继续往下,还是4个区间。
因为线段树的高度为log(n),所以查询的时间复杂度为O(log(n))
代码2:线段树区间查询模板
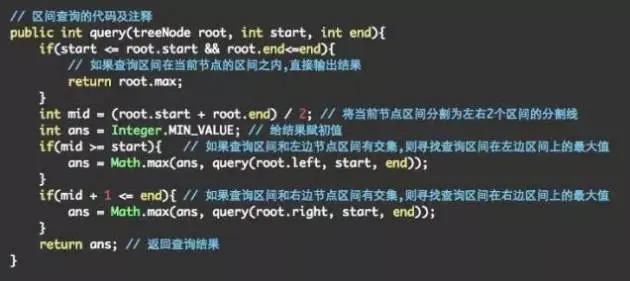
单点更新:更新序列中的一个节点
如何把这种变化体现到线段树中去?

例如,将序列中的第4个点更新为5,要变动3个区间中的值,分别为[3,3],[2,3],[0,3]

可以这样想,改动一个节点,与这个节点对应的叶子节点需要变动。因为叶子节点的值的改变可能影响到父亲节点,然后叶子节点的父亲节点也可能需要变动。
所以需要从叶子节点一路走到根节点,去更新线段树上的值。因为线段树的高度为log(n),所以更新序列中一个节点的复杂度为log(n)。
代码3:线段树单点更新模板
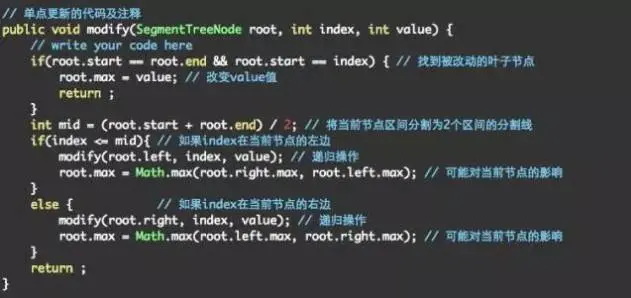
如果需要区间的最小值或者区间的和。和构造的时候同理。
相关Lintcode面试题
线段树构造
www.lintcode.com/zh-cn/probl…
www.lintcode.com/zh-cn/probl…
线段树单点更新
线段树区间查询
www.lintcode.com/zh-cn/probl…
www.lintcode.com/zh-cn/probl…
线段树综合
www.lintcode.com/zh-cn/probl…
www.lintcode.com/zh-cn/probl…
www.lintcode.com/zh-cn/probl…
www.lintcode.com/zh-cn/probl…
www.lintcode.com/zh-cn/probl…
欢迎关注我的微信公众号:九章算法(ninechapter)。
精英程序员交流社区,定期发布面试题、面试技巧、求职信息等
