前言
堆又称为优先队列，支持插入和删除堆顶操作；
分为最小堆、最大堆、还有一种扩展实现对顶堆，常用语实时获取中位数；
在贪婪算法的实现即是基于堆，该算法通过反复最小元来进行操作；
下虑插入
下虑插入主要用在delete操作，此时顶刚好空缺并且堆中少了一个元素,因此现在堆中最后一个元素(暂且命名为X)必须移动到该堆的某个位置。
如果X可以放入堆顶，那么delete操作完成。
但是这一般不太可能，因此我们将空缺位置的两个儿子中优先级(根据最大堆或者最小堆优先级可能不同)更大与空缺位置调换；此时空缺位置被推向想一层。重复改步鄹直到X可以放入空缺位置。
这种一般的策略叫做下虑；
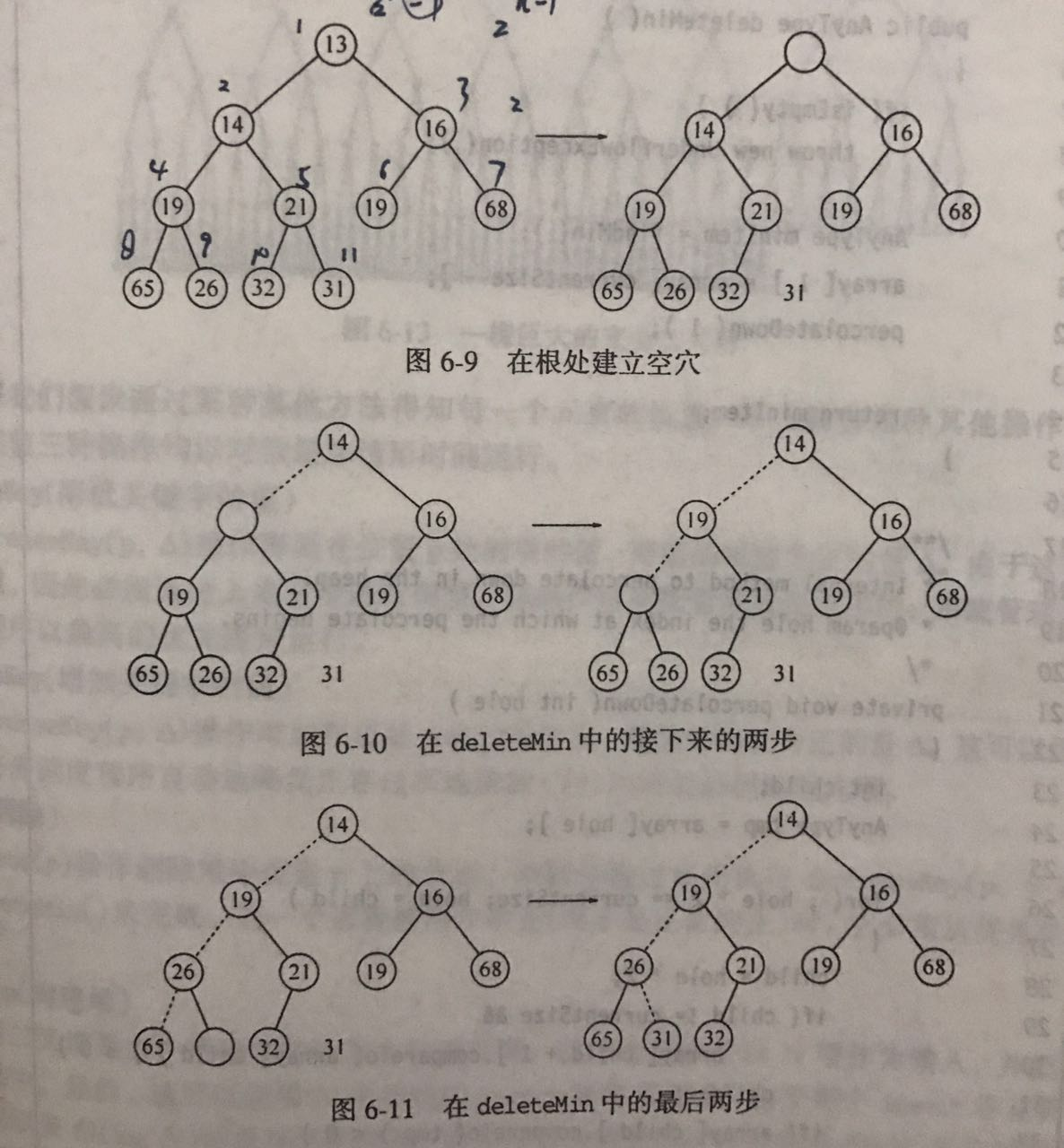下虑插入示意图
上虑插入
上虑插入主要用于insert操作，此时堆中处于平衡状态，因此现在在堆尾建立一个一个空缺位置；
在空缺位置与其父节点进行对比优先级，若插入元素优先级更高，则将空缺位置与父节点调换位置；
此时空缺位置已被推上一层，重复吃步鄹直到找到合适的空缺位置。
这种一般的策略叫做上虑；
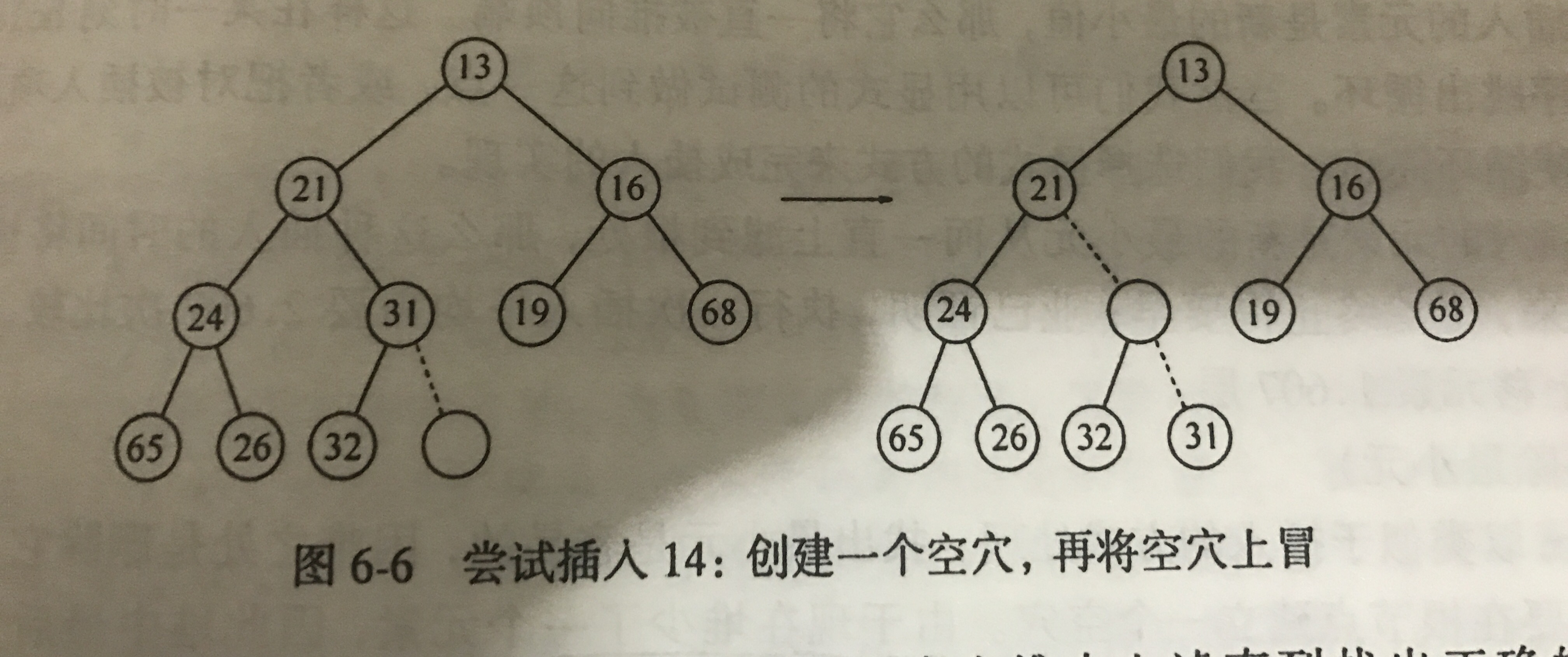上虑插入示意图1 
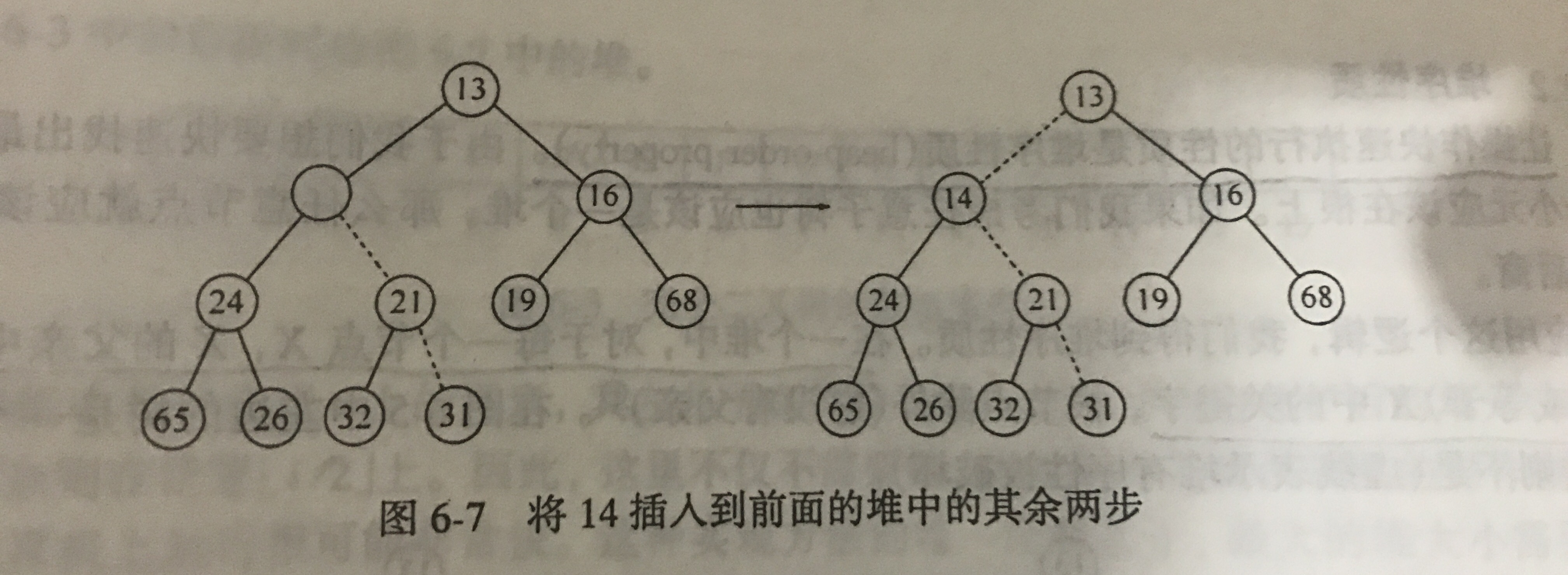上虑插入示意图2
代码
go
package adt
import "fmt"
// Heap 堆结构
// 数组形式为index为0的元素默认为空，总index为1元素开始
// 方便定位元素
// 即如往堆里插入1,2,3,4,5
// 数组元素为[0,1,2,3,4,5]
type Heap struct {
array []int
isMax bool // 表示最大堆还是最小堆
}
// GetHeap 获取一个Heap实列
func GetHeap(isMax bool) *Heap {
return &Heap{array: make([]int, 1, 8), isMax: isMax}
}
// Insert 插入一个元素
func (h *Heap) Insert(value int) {
if h.array == nil {
h.array = make([]int, 1, 8)
}
h.array = insert(h.array, value, h.isMax)
}
// Delete 删除并获取堆顶
func (h *Heap) Delete() (top int, err error) {
h.array, top, err = reset(h.array, h.isMax)
return top, err
}
// getCompareResult 比较
func getCompareResult(o1, o2 int, isMax bool) int {
if o1 == o2 {
return 0
}
if isMax {
if o1 > o2 {
return 1
}
return -1
}
if o1 < o2 {
return 1
}
return -1
}
//
//
// Insert 相关函数
//
//
// insert 根据堆性质想数组中插入一个元素
func insert(array []int, value int, isMax bool) (nowArray []int) {
nowArray = append(array, 0)
insertIndex := getInsertIndex(nowArray, len(array), value, isMax)
nowArray[insertIndex] = value
return nowArray
}
// getInsertIndex 递归获取插入元素的数组下标
// 使用上虑策略
func getInsertIndex(array []int, nowIndex int, value int, isMax bool) int {
if nowIndex < 2 {
return 1
}
faIndex := getFaIndex(nowIndex)
if getCompareResult(array[faIndex], value, isMax) >= 0 {
return nowIndex
}
array[faIndex], array[nowIndex] = array[nowIndex], array[faIndex]
return getInsertIndex(array, faIndex, value, isMax)
}
// getFaIndex 获取一个元素的父级元素数组下标
func getFaIndex(index int) int {
return index / 2
}
//
//
// Delete 相关函数
//
//
const (
noGo = iota
goLeft
goRight
)
// reset 重设置一个数组
func reset(array []int, isMax bool) (nowArray []int, topValue int, err error) {
lastIndex := len(array) - 1
if lastIndex == 1 {
topValue = array[1]
nowArray = array[:lastIndex]
return
} else if lastIndex < 1 {
return array, 0, fmt.Errorf("堆中已无元素")
}
topValue, array[1] = array[1], 0
value := array[len(array)-1]
nowArray = array[:len(array)-1]
lastInsertIndex := getLastInsertIndex(nowArray, 1, value, isMax)
nowArray[lastInsertIndex] = value
return
}
// getLastInsertIndex 下虑
func getLastInsertIndex(array []int, nowIndex int, value int, isMax bool) int {
status := noGo
lastIndex := len(array) - 1
leftIndex, rightIndex := getSonIndex(nowIndex)
if lastIndex >= rightIndex {
left, right := array[leftIndex], array[rightIndex]
status = getStatus(left, right, value, isMax)
} else if lastIndex == leftIndex && getCompareResult(array[leftIndex], value, isMax) >= 0 {
status = goLeft
}
switch status {
case noGo:
return nowIndex
case goLeft:
array[nowIndex], array[leftIndex] = array[leftIndex], value
return getLastInsertIndex(array, leftIndex, value, isMax)
case goRight:
array[nowIndex], array[rightIndex] = array[rightIndex], value
return getLastInsertIndex(array, rightIndex, value, isMax)
}
panic("--")
}
// getSonIndex 获取一个元素的左右子元素数组下标
func getSonIndex(index int) (left, right int) {
return 2 * index, 2*index + 1
}
// getStatus 根据三个值获取走那边获取步鄹
func getStatus(left, right, value int, isMax bool) (res int) {
res = 0
if getCompareResult(left, value, isMax) > 0 || getCompareResult(right, value, isMax) > 0 {
res++
} else {
return
}
if getCompareResult(right, left, isMax) > 0 {
res++
}
return
}总结
插入时间复杂度：O(logN)
堆的实现确实惊为天人，如何的有魅力。
特别是上虑与下虑策略的思想，真是让人大开眼界。
最后更新时间：
