本文由北邮@爱可可-爱生活 老师推荐，阿里云云栖社区组织翻译。
以下为译文
机器学习理论——part I 前言 （第II部分内容点此；第III部分内容点此 ）
动机
大多数人在小的时候被魔术师以及魔术技巧所迷住，并想弄明白其中的奥秘。有些人会带着这份迷恋研究到更深处并学习魔术技巧，有些人会接受专业的训练，而其他人会继续平庸下去。我在年幼时也尝试过魔术技巧并沉迷于其中，然而后来 学习 的是 另外一种魔术，称作计算机编程。
编程确实酷似魔法， 和魔术一样，自学的现象在计算机编程世界占了上风。在过去的两年计算机开发者调查显示，超过一半的 开发者是无师自通 。我 是在全职工作外学习这些计算机科学知识，当你已经工作后再尝试学习这些科目会是相当大的一个挑战 。
如今我们可以找到很多关于计算机科学的视频、文章、博客以及自定进度点播MOOC 课程，这几乎涉及每个方面。其中很多写的很详细并解释得很清楚，而且 可以自由访问。这些资源的存在使得自我学习过程更加全面，使工作/ 生活 / 学习的平衡更易于管理，不幸的是，这 并 不是学习编程的完全正确趋势。
机器学习
虽然在大二就开始自学机器学习，但当毕业后才意识到自己错过了许多基础知识。所以在同样情形下，我很高兴发现自己避免了这种情况的发生，但机器学习理论不像计算机科学世界那么容易驯服。 虽然互联网上充满了学习资源，但理论方面的内容是不一样的。即使你可以找到书籍、讲义、甚至是全部的讲座，但大多数不能像一系列博客、短视频或者MOOC 提供的灵活性。
本文根据作者本身学习计算机科学的经验，给出了学习机器学习理论的这一系列文章，能够填补自主学习机器学习的理论与实践之间的差距，从而在征途上少一些艰辛。
这个系列是为了谁？
该系列意图是为了给机器学习理论方面提供简单的介绍，这将会对你是有利的，如果你是：
l 机器学习的从业者，并想深入了解详细过程；
l 机器学习的学生，尝试深入钻研机器学习理论并会喜欢一些宽松政策；
如果你是机器学习的初学者，这可能不是你的最佳起点。使用实际教程开始会更好。当你掌握了机器学习实践的窍门后，如果你觉得有必要，可以回到这里。
先决条件
理论需要数学知识，机器学习的理论也不例外。但是由于这仅仅是为了简单的介绍，不会钻研太深的数学分析，将更加注重理论的直觉与足够的数学知识以为了保持严谨。
大多数所需要的知识是：概率和随机变量，和微积分的基本知识。
注意事项
我仍然不是这个领域的专家，所以当你在这个系列中发现一些错误，请让我知道；
这仅仅是一个简单介绍，如果你想真正理解该领域，在阅读该系列的同时也要努力工作；
现在将机器学习问题快速公式化，以便建立起数学模型和框架
形式化学习问题
在这个系列中，将主要侧重有监督学习问题，数据集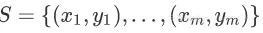
，其中
xi
是特征向量，yi
是标签，问题是给定xi
，怎么得到yi
的值。比如说
xi
是具体医学测量结果的特征向量， yi
是病人是否为糖尿病，我们希望从给定的医学测试结果中诊断是否患有糖尿病。
为了建立理论框架，重新梳理下已经知道的内容
1 知道从众多人口中随机采样的数据集中的值（xi,yi ），具体的例子中的数据集是从众多可能患者中随机采样得到
将该例子公式化，两个随机变量X 和 Y 表示 xi 与 yi ，且概率分布分别为 P(X) 和P(Y)；
2 我们知道X 与 Y 之间有一些规则，并希望任意的 XY 对都能符合该规则， 定义该规则，正式将其称为空间，X 是从输入空间 X 中取值得到， Y 是从输出空间 Y 取值得到；
3 特征值与标签之间有一定的联系，在某种程度上，特征值决定标签值，或者说Y 的值是以 X 值为条件；
正式地，将其称作条件概率 P （ Y|X ），利用该概率可以得到其联合概率密度 P(X|Y) ；
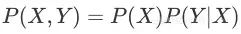
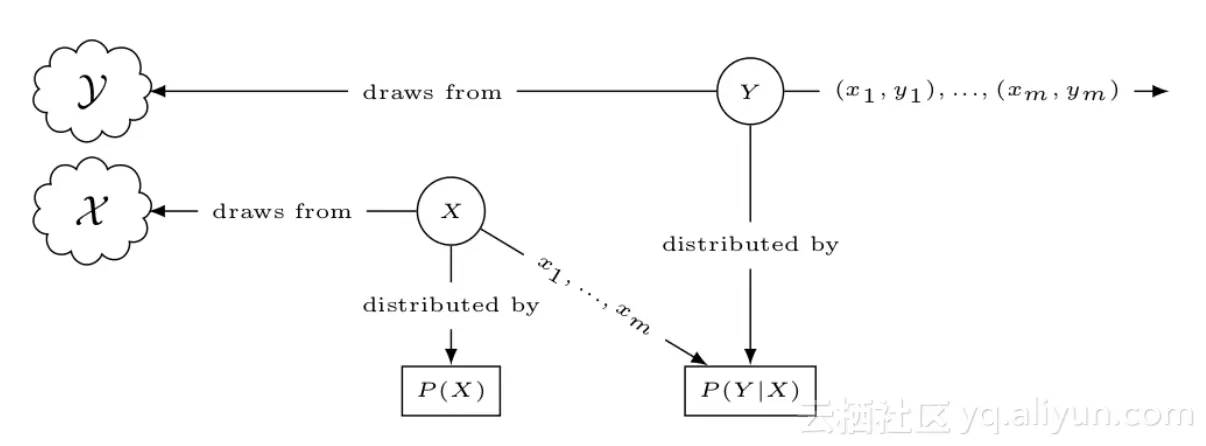
根据这三点，可以定义统计模型，下图形式化的描述了模型的处理过程
目标函数
机器学习过程的根本任务是理解条件概率分布P （ Y|X ）的性质，为了避免麻烦，下面介绍一些简单的工作。
可以使用均值和方差分解一个随机变量，均值是随机变量的中心，方差是测量随机变量在均值周围是如何分布。假设给定随机变量V 和 W ，则
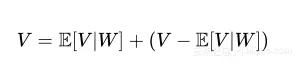
其中E[V|W] 是随机变量 V 给 W 的条件均值，该均值可以将 V 的值分解为两部分。 任意W 与 V 的相关联值（ wi,vi ）的关系可以定义如下
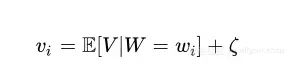
ζ 表示噪声变量ζ 的值 ，称为噪声分量，同样地定义统计模型（ xi ， yi ）
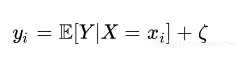
其 f : X → Y的函数定义如下
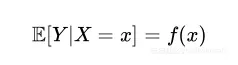
即条件概率是输入空间X 映射到输出空间 Y 的函数，使用下列公式表示特征与标签的联系
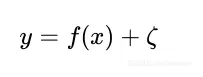
目标函数为f=f(x) ，统计模型简化为
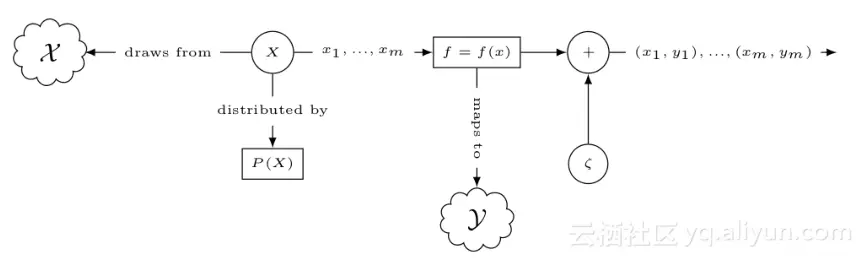
机器学习的任务简化为估计函数f 。
假设
由于要对现存的每个函数进行评估，因此尝试对函数f 进行假设，定义函数可能的空间为假设空间 H 。
如果假设函数f 是来自 ax+b ，可以定义假设空间 H 为
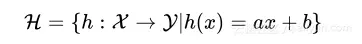
这是所有函数h 映射输入空间到输出空间的集合，机器学习的任务现在是从 H 中挑选出一个具体的函数 h ，该函数能够最好的估计目标函数 f 。
损失函数
损失函数是用来评估假设函数估计目标函数的效果如何，定义损失函数（代价函数）
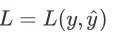
该函数是将从特征向量x 中得到的估计标签 y 与真实标签 y 的差距
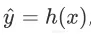
使用损失函数可以计算假设函数h 对整个数据集的性能，分类错误或者经验风险定义为
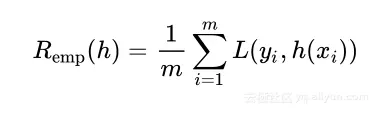
在这里不称作经验误差的原因是如果使用E 表示误差，这会导致与期望值 E 标记的混乱，因此使用风险和 R 代替。通过定义的经验误差，机器学习过程需要选择最小的 Remh(h) 作为目标函数 f 的最优估计。
泛化误差
我们的目标是学习总体数据集的概率分布，这意味着假设应该对采样出的新数据也会有低的错误。这也说明这些表现好的假设在总体概率分布上有好的泛化，定义泛化误差：
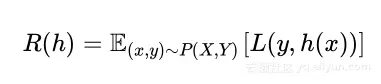
学习问题是否可解？
如果 Remp(h) 和 R(h) 非常接近，那么学习问题可解。问题转化为计算下述概率：
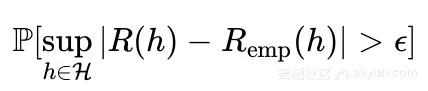
公式表示
R与Remp
之间的绝对差的最小上界大于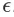
的概率，若该概率足够小，则学习问题可解。
参考文献：
l James, Gareth, et al. An introduction to statistical learning. Vol. 6. New York:springer, 2013.
l Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. Springer, Berlin: Springer series in statistics, 2001.
l Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. Foundations of machine learning. MIT press, 2012.
l Abu-Mostafa, Y. S., Magdon-Ismail, M., & Lin, H. (2012). Learning from data: ashort course
文章原标题《Machine Learning Theory - Part I》，作者：Mostafa Samir，译者：海棠
文章为简译，更为详细的内容，请查看 原文
