但这篇文章真的太简略了，其中编译器前端最重要的文法分析只是一笔带过，没有介绍任何理论和方法，虽然最后确实实现了一个超简单的编译器，但我感觉还远远不够。
这段时间闲着没事的时候去详尽地学了学编译原理，自己也实现了一个很简单的编译器（至少比上面那个稍微复杂一点），所以就用这篇文章记录一下吧。
当然我自己水平有限，肯定不如专门做编译器的巨巨那样熟悉西方的那一套的理论，所以这篇文章面向的读者大概是『没系统接触过编译原理的、看得懂JavaScript的程序员』。
零、目标及动机
DEMO的地址在这里：
starkwang.github.io/naive-compl…/
我们的目标是实现一个把C风格算式转换为Lisp风格的编译器，比如：
'1 + 2' => '(+ 1 2)'
'1 + 2 * 3' => '(+ 1 (* 2 3))'
'(1 + 2) * 3' => '(* (+ 1 2) 3)'
事实上编译原理已经深入到前端开发的各个角落，比如 React 的 JSX 语法，它是需要编译到普通的 JS 才能正常运行的：
// JSX语法
<MyComponent foo="0">
<Child1 foo="1">Hello</Child1>
<Child2 foo="2"/>
</MyComponent>
// 实际运行时需要被转换为下面这样的代码：
React.createElement(
MyComponent,
{foo: "0"},
React.createElement(Child1, {foo: "1"}, "Hello"),
React.createElement(Child2, {foo: "2"})
);
还有每次发布部署的时候一般都会做压缩混淆代码，这从性质上讲也是一种『编译』：
// 源码：
function myLongAndStupidFunctionName(){
doSomeThing();
}
function doSomeThing(){
//......
}
// 压缩混淆之后：
function a(){b();}function b(){/*......*/}
还有诸如Babel、TypeScript、Flow、Webpack2的Tree-Shaking等等等等，就不再列举了，总之学一点编译原理总是能派上用场的。
一、编译器的大致结构
那么就开始吧，首先我们先了解一下编译器大概的结构，我们使用括号来标注某个过程：
输入字符串
->（词法分析器tokenizer）-> 符号串
->（文法分析器parser）-> 抽象语法树AST
->（后端代码生成）-> 目标代码字符串
举个例子，比如我们希望把『1 + 1』这段代码转换为『(+ 1 1)』，那么首先词法分析器会将代码转换为一串 token：
var token = tokenizer('1 + 1');
//=> ['1', '+', '1']
// 实际上这样表达会更严谨，但为了方便起见，我们还是用上面那样简单的表示法
// [
// {type: 'NUMBER', value:'1'},
// {type: 'OPERATOR', value:'+'},
// {type: 'NUMBER', value:'1'}
// ]
然后就是文法分析的过程，由符号串生成一个AST：
var ast = parser(token);
//=>
// {
// type: 'root',
// child: [{
// type: 'number',
// child: ['1']
// }, {
// type: 'operator',
// child: ['+']
// }, {
// type: 'number',
// child: ['1']
// }]
// }
// 不同的文法以及分析方法会有不同的AST结构，上面只是一个范例
有了这个AST之后，我们可以对它做任何想做的事情，比如生成Lisp风格的表达式：
var code = transformer(ast);
//=> '(+ 1 1)'
二、词法分析和Tokenizer
编译器的第一个部分是 Tokenizer，它的作用是把输入的字符串转换为一个由 token 组成的集合：
tokenizer('(11 + 22) * 33')
//=> ['(', '11', '+', '22', ')', '33']
/**
* 由于我们这个编译器的合法输入字符极其有限，只有数字、括号、加减乘除，
* 所以没有使用更抽象的对象（比如 {type: 'NUMBER', value: '1'} 这样的结构）
* 去表示每一个 token，直接使用字符串会稍微简化后面的流程。
**/
是的，Tokenizer 的实现一点都不难，它本质上是一个有限状态机（DFA），在这里只是切割了一下字符串，它也不是这篇文章的重点，所以就不贴代码上来了，具体代码可以看这里（当然存在比我更好更优雅的实现）：
https://github.com/starkwang/naive-complier/blob/master/tokenizer.js
三、文法分析和Parser
1、文法的基本概念
文法分析才是这篇文章的重点，什么是文法呢？文法就是一组规则，它定义了哪些符号串是合法句子，比如有一种语言的文法如下：
A -> Ab
| a
它表示，『A』这个符号可以派生出『Ab』，也可以派生出『a』，我们把这样能生出其它符号的符号称为“非终结符”；同理，a和b不能生出符号，所以称为“终结符”。
为了方便说明，后面出现的非终结符一般使用大写字母开头，而终结符使用小写字母。
上面这个简单的文法可以派生出诸如『ab』、『abb』、『abbbbbbb』这样的符号串。按照同样的思路我们很容易就能写出一个普通四则运算的文法：
Expr -> Expr op Factor 规则1
| Factor 规则2
op -> + 规则3
| - 规则4
| * 规则5
| / 规则6
Factor -> (Expr) 规则7
| num 规则8
根据这个文法，可以生成所有的四则运算表达式，比如连续使用规则1、5、7、1、3、8......展开生成式，就能得到『num * (num + num)』
Expr
->（规则1）-> Expr op Factor
->（规则5）-> Expr * Factor
->（规则7）-> Expr * (Expr)
->（规则1）-> Expr * (Expr op Factor)
->（规则3）-> Expr * (Expr + Factor)
->（规则8）-> Expr * (Expr + num)
->（....）-> num * (num + num)
由它展开的AST是这样的：
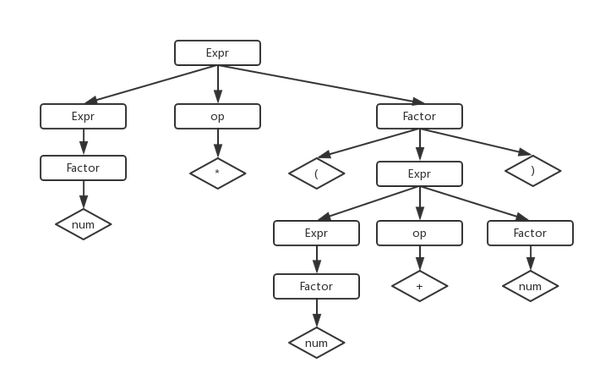
2、消除文法的歧义
上面的例子很简洁明了，看起来没有什么问题。那么我们现在考虑一下大部分类Algol语言使用的『if-then-else』这种结构的文法，直觉上它的文法是：
Statement -> if Expr then Statement else Statement
| if Expr then Statement
| CodeBlock
看起来是对的，但如果有这样的输入符号串，就会导致歧义：
if Expr1 then if Expr2 then CodeBlock1 else CodeBlock2
// 语义1
if Expr1
then if Expr2
then CodeBlock1
else CodeBlock2
// 语义2
if Expr1
then if Expr2
then CodeBlock1
else CodeBlock2
发现了吗？问题在于最后那个『else CodeBlock2』，我们无法知道它究竟是和哪一个『if』配对，这直接导致了歧义的文法，是没有办法分析的。
所以我们需要纠正这种文法上的缺陷，这就需要重写我们的文法，比如我们可以把文法改写成下面这样：
Statement -> if Expr then WithElse else Statement 规则1
| if Expr then Statement 规则2
| CodeBlock 规则3
WithElse -> if Expr then WithElse else WithElse 规则4
| CodeBlock 规则5
然后之前的歧义问题就会得到消除：
Statement
->（规则2）-> if Expr then Statement
->（规则1）-> if Expr then if Expr then WithElse else Statement
->（规则3）-> if Expr then if Expr then WithElse else CodeBlock
->（规则5）-> if Expr then if Expr then CodeBlock else CodeBlock
3、文法的结构优先权
仅仅把文法的歧义消除是远远不够的，下面我们回到四则运算表达式上，假设有一个这样的输入：
num - num * num
如果用之前的那种文法，稍微推导一下，就会发现展开后的AST是这样的：
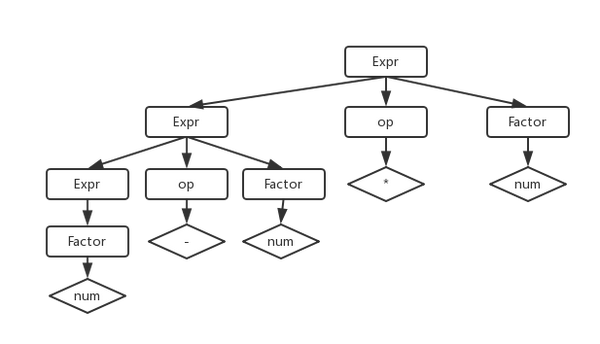嗯，这里我们错误地把前三个符号『num - num』解析成了一个独立的表达式，也就是说我们把输入识别成为了『(num - num) * num』这种形式，这和数学中的运算法则是不符的，因为乘除法的优先级是高于加减法的。
解决方法和之前一样，我们需要改写我们的文法，赋予乘除法更高的优先级（但不能高于括号），于是我们可以写出下面这样严谨的文法：
Expr -> Expr + Term
| Expr - Term
| Term
Term -> Term * Factor
| Term / Factor
| Factor
Factor -> (Expr)
| num
好的，这个文法完全没有错误了，但它仍然有一些小缺陷，下面我们继续。
4、递归下降分析、消除左递归
有了正确严谨的文法，下面我们要进入真正的文法分析阶段了。下面我们要介绍的是『自顶向下、递归下降』的分析方法，考虑这样一种极简单的文法：
A -> aB
B -> bB
| null
看起来是不是有点眼熟？额。。。先别管眼不眼熟，我们通过这个文法可以比较简单地构建出一个递归下降的分析器：
// 一个极简的递归下降分析器
function parser(token) {
var i = 0;
function nextWord() {
return token[i++];
}
var word = nextWord();
if (A() && !word) {
return true;
} else {
return false;
}
/**
* A -> aB
**/
function A() {
if (word == 'a') {
word = nextWord();
return B();
} else {
console.error('Unexpected token:', word);
}
}
/**
* B -> bB
* | null
**/
function B() {
if (word == 'b') {
word = nextWord();
return B();
} else if (!word){
word = nextWord();
return true;
} else {
console.error('Unexpected token:', word);
}
}
}
parser(['a', 'b']); //=> true
parser(['a', 'b', 'b', 'b']); //=> true
parser(['a', 'a', 'b', 'b']); //=> false
你应该发现了，这个递归下降的分析器接受类似『ab......b』这样的串，对应的文法就是我们在这一章节最开始给出的那个超简单的文法（叫它文法1好了）：
// 文法1
A -> Ab
| a
但我们递归下降分析器使用的是另一种等价的文法（叫它文法2）：
// 文法2
A -> aB
B -> bB | null
这两种文法派生出的串是完全一样的，那区别何在呢？
区别就在于『是否存在左递归』，在文法1里，A的第1个生成式（A -> Ab）最左边出现了它自己，如果我们使用文法1构建一个递归下降分析器，那么函数A会这样写的：
// 使用含有左递归的文法1
function A(){
if(A()){
return word == 'b';
} else if(word == 'a'){
word = nextWord();
return true
}
}
是的，这显然出现了一个死循环，分析器读入了一个a，然后陷入了无限调用A函数的递归中。所以对于一个递归下降的分析器来说，是需要消除掉左递归的。对于文法1这样含有左递归的文法，我们需要将它改写为文法2的形式。
后面的文章里你会看到，对于LL(1)分析器，由于需要计算First集，也同样需要消除左递归（什么时候有后面的文章？不知道大概明年吧=_=）
好，那么我们再看看我们之前的四则运算文法有没有左递归：
Expr -> Expr + Term （左递归）
| Expr - Term （左递归）
| Term
Term -> Term * Factor （左递归）
| Term / Factor （左递归）
| Factor
Factor -> (Expr)
| num
Expr -> Term + Expr
| Term - Expr
| Term
Term -> Factor * Term
| Factor / Term
| Factor
Factor -> (Expr)
| num
这就是终极无敌版文法了！那么下面只需要根据这个文法依葫芦画瓢，模仿之前那个极简版的递归下降分析器，写一个稍微更复杂点的就行了！
function parser(token) {
var i = 0;
function nextWord() {
return token[i++];
}
var word = nextWord();
if (Expr() && !word) {
return true;
} else {
return false;
}
/**
* Expr -> Term + Expr
* | Term - Expr
* | Term
**/
function Expr() {
if (Term()) {
if (word == '+' || word == '-') {
word = nextWord();
return Expr();
} else {
return true;
}
}
}
/**
* Term -> Factor * Term
* | Factor / Term
* | Factor
**/
function Term() {
if (Factor()) {
word = nextWord();
if (word == '*' || word == '/') {
word = nextWord();
return Term();
}
return true;
}
}
/**
* Factor -> (Expr)
* | num
**/
function Factor() {
if (word == '(') {
word = nextWord();
if (Expr()) {
return word == ')';
}
} else if (isNumber(word)) {
return true;
}
}
function isNumber(word) {
return /^\d+$/.test(word);
}
}
parser(['(', '1', '+', '2', ')', '*', '3']) //=> true
等一下，好像漏了什么。。。说好的生成AST树呢？
其实吧，既然递归下降已经写好了，现在只需要在递归分析的过程中加入一点生成树的代码就行了，例如Expr函数可以变成这样：
function Expr() {
// 生成一个新的节点Expr
var node = new Node('Expr');
// 向指针p指向的节点（父节点）的child中加入这个新节点
p.child.push(node);
// 指针p指向新节点
p = node;
if (Term()) {
// Term()过程中p的指向可能被改变了，我们重置一下
p = node;
if (word == '+' || word == '-') {
p.operator = word;
word = nextWord();
return Expr();
} else {
return true;
}
}
}
同理，每个函数都类似这样改写，就会得到最终的文法分析器代码，完整版的在这里：
https://github.com/starkwang/naive-complier/blob/master/parser.js
是的！我们完成了最蛋疼的文法分析部分，下面代码生成就和喝水一样简单了。
四、代码生成
这块简单多了，和递归分析同样的思路，我们只需要读入根部节点，用一个递归遍历AST，判断出每个节点派生子节点所使用的文法，然后返回相应的字符串就行了：
function transformer(root) {
return transformExpr(root.child[0]);
}
function transformExpr(Expr) {
if (Expr.operator) {
// Expr -> Expr + Term
// | Expr - Term
return `(${Expr.operator} ${transformTerm(Expr.child[0])} ${transformExpr(Expr.child[1])})`;
} else {
// Expr -> Term
return transformTerm(Expr.child[0]);
}
}
function transformTerm(Term) {
if (Term.operator) {
// Term -> Term * Factor
// | Term / Factor
return `(${Term.operator} ${transformFactor(Term.child[0])} ${transformTerm(Term.child[1])})`;
} else {
// Term -> Factor
return transformFactor(Term.child[0]);
}
}
function transformFactor(Factor) {
if (Factor.child[0].type == 'Expr') {
// Factor -> (Expr)
return transformExpr(Factor.child[0])
} else {
// Factor -> num
return Factor.child[0];
}
}
这一块其实也不是重点，因为都已经得到一个完整的AST了，想对它做什么都是可以的，生成代码只是一个小功能而已。
五、结尾
好了，这就是一个比较完整的小型编译器了，现在文法只有简单的几条，只能转换四则运算表达式，如果扩展一下文法的话，当然还可以转换其它任意的代码，甚至去写一个JSX编译器也不是太难了。
我记得之前在知乎上看到过一个问题，现在已经找不到了，大致意思是问『作为不做编译器开发的程序员，需要懂多少编译原理？』
下面最高赞的观点大概是『能手写tokenizer、能根据文法写出递归下降的parser就足够了。』
今天这第一篇文章也恰好达到了这个水准，但这也只是编译理论的沧海一粟而已，接下来的文章里我想介绍一下 LL、LR 以及 SLR 等等更加先进的文法分析方法（大学最后一个期末季要来了，估计要元旦之后才能写完了）。
