注:以下所有排序算法都是按照整数值从小到大排序。
冒泡排序
思想:对于一个序列,走一趟把最大数冒到最后面。
示例:对于序列4, 10, 1, 6, 2, 7, 3, 8如下图(红框表示下一趟需要处理的子序列)
即总共需要走n趟,当第i趟走完时倒数i个数是有序的。
for(i = 0; i < n; i++) {
for(j = 0; j < n - i - 1; j++) {
if(a[j] > a[j + 1]) {
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}优化:由上面的示意图可知,当第4趟走完时序列已经完全排好序了,后面的几趟都是多余的。因此可以弄一个标记变量,假如在某一趟中没有发生交换则说明对于任意两个相邻的元素都满足前者<后者,也就是序列已经排好序了,因此可以提前结束。< p="">
时间复杂度:O(n^2),空间复杂度O(1),稳定性:稳定。
总结:走n趟,第i趟将前n-i+1个元素的最大数冒到最后面。
选择排序
思想:对于一个序列,走一趟就把选到的最小数放在该序列的最前面。
示例:对于序列4, 10, 1, 6, 2, 7, 3, 8如下图
for(i = 0; i < n; i++) {
int index = i;
for(j = i; j < n; j++) {
if(a[j] < a[index]) {
index = j;
}
}
if(index != i) {
int temp = a[index];
a[index] = a[i];
a[i] = temp;
}
}时间复杂度:O(n^2),空间复杂度O(1),稳定性:不稳定。
总结:走n趟,第i趟将后n-i+1个元素的最小数选择放到最前面。
插入排序
思想:对于后面n-1个数,依次插入到前面的有序序列。
示例:对于序列4, 10, 1, 6, 2, 7, 3, 8如下图
代码(直接插入法)
for(i = 1
for(j = i - 1
if(a[j + 1] < a[j]) {
int temp = a[j]
a[j] = a[j+1]
a[j+1] = temp
} else {
break
}
}
}时间复杂度:O(n^2),空间复杂度O(1),稳定性:稳定。
总结:将后n-1个元素逐个插入到前面的有序序列中
快速排序
思想:分治排序每一部分,而排序采用partition方法进行。
示例:对于序列4, 10, 1, 6, 2, 7, 3, 8。Partition过程:
int partition(int a[], int left, int right) {
if(left > right || left < 0) {
return -1;
} else {
int base = a[left];
int low, high;
low = left;
high = right;
while(low < high) {
while(low < high && a[high] >= base) {
high--;
}
if(low < high) {
a[low] = a[high];
low++;
}
while(low < high && a[low] < base) {
low++;
}
if(low < high) {
a[high] = a[low];
high--;
}
}
a[low] = base;
return low;
}
}
void quickSort(int a[], int left, int right) {
if(left < right) {
int mid = partition(a, left, right);
quickSort(a, left, mid - 1);
quickSort(a, mid + 1, right);
}
}时间复杂度:最好情况O(nlogn),最坏情况O(n^2),平均情况O(nlogn)。空间复杂度:所需栈空间O(logn)~O(n)。稳定性:不稳定
堆排序
思想:利用堆进行调整使得堆上的元素有序。
代码:
void siftDDown(int a[], int p, int len) {
int temp;
int child = 2 * p + 1;
while(child < len) {
if(child + 1 a[child + 1]) {
child++;
}
if(a[p] > a[child]) {
temp = a[p];
a[p] = a[child];
a[child] = temp;
p = child;
child = 2 * p + 1;
} else {
break;
}
}
}
int main()
{
int a[] = {4, 10, 1, 6, 2, 7, 3, 8};
int n = 8;
int i;
for(i = n/2 - 1; i>= 0; i--) {
siftDDown(a, i, n);
}
for(i = n - 1; i >= 0; i--) {
cout<
时间复杂度:最好情况O(nlogn),最坏情况O(nlogn),平均情况O(nlogn)。空间复杂度:O(1)。稳定性:不稳定
归并排序
代码:
void merge(int a[], int start, int mid, int end) {
if(start > mid || mid + 1 > end) {
return;
}
int p = start, q = mid + 1;
int *temp = new int[end - start + 1];
int k = 0;
while(p <= mid && q <= end) {
if(a[p] <= a[q]) {
temp[k++] = a[p++];
} else {
temp[k++] = a[q++];
}
}
while(p <= mid) {
temp[k++] = a[p++];
}
while(q <= end) {
temp[k++] = a[q++];
}
for(int i = start; i <= end; i++) {
a[i] = temp[i - start];
}
delete []temp;
}
void mergeSort(int a[], int start, int end) {
if(start < end) {
int mid = (start + end) / 2;
mergeSort(a, start, mid);
mergeSort(a, mid + 1, end);
merge(a, start, mid, end);
}
}
时间复杂度:最好情况O(nlogn),最坏情况O(nlogn),平均情况O(nlogn)。空间复杂度:O(n)。稳定性:稳定
几种排序算法对比
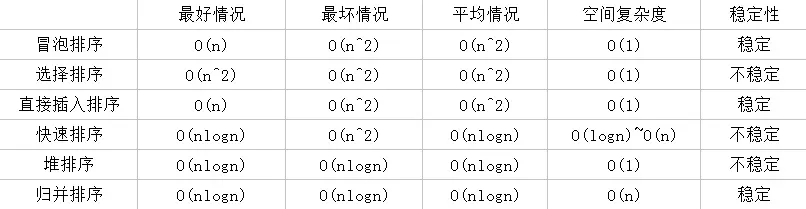
说明:如果最好情况与最坏情况的时间复杂度不一样,则说明初始数据集的排列顺序对该算法的性能有影响。
转载请注明出处:blog.csdn.net/u012619640/…