比喻、图表、案例、通俗解释再到技术细节,逐步攻克复杂概念
本文翻译自 Kalid 介绍其 ADEPT 学习法的 博文。「Adept」原意是“内行、熟手”的意思,这里为了生动形象,将「ADEPT 学习法」译作了「聚焦学习法」。
为简化和通顺文字,有大量意译和部分删减。
首先让我们用一句话解释「聚焦学习法」:按照比喻、图表、案例、通俗解释,最后到技术细节的顺序,逐步掌握一个复杂的概念。
- 比喻:告诉我看起来像什么
- 图表:给我一个直观的印象
- 案例:让我直接感受一下它
- 通俗解释:尝试用大白话描述它
- 技术细节:最后再正式探讨细节
现在让我们具体了解一下,当你学习复杂概念,或向他人进行解释时,该怎样运用各个步骤。
比喻:它看起来像什么?
多数新的概念不过是已知概念的变形、扩展和组合,所以从比喻开始最为合适。
在数十年的生命历程中,我们其实已经掌握了无数概念,其中必然有一个与新的概念大致相似,可作为我们学习的起点。
以”虚数”举例,大多数课程都会直接空洞而简单地解释道:“负数也可以有平方根”。额,不如让我们换个方式:
- 人们直到十七世纪都还怀疑负数的存在:比一无所有还少的是什么呢?
- 直到我们意识到所有数字都在一条数轴上,从零点出发,可以向前移动也可以向后。
- 而虚数的概念只是告诉我们,其实还可以向上或向下移动,甚至围绕着数轴旋转。就这么简单!
比喻通常是模糊的,并非 100% 准确,但它极其有用。它们是帮助你过河的竹筏,渡过之后随时可以丢弃。
图表:利用上另一半大脑
我们通常认为图表只是一种辅助,帮助不够强的你理解艰深的符号。然而事实上,虚数的相关研究进展也是在形象的图表传播开来之后!
让我们从最容易的解释开始,文字、图表、或是解释性的舞蹈都行。
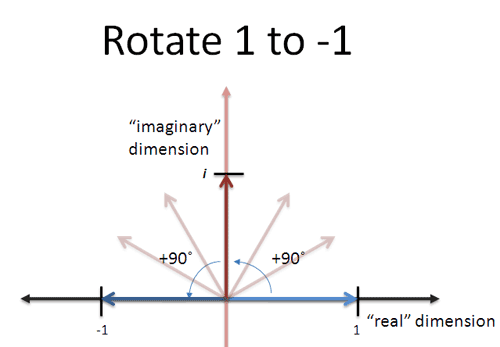
虚数让我们可以围绕着数轴旋转,而不再是从一边移动到另一边。
从视觉上找到了点感觉吧?
我们大脑的另一半更善于视觉处理,让我们把它利用起来~(顺便一提,对于这个话题,解释性的舞蹈同样有效)
案例:让我体验一下概念
现在可以把“虚数”这个炫酷的概念拋给学生了?
千万别。不要试图告诉别人感觉是怎样的,要让他们亲身体验。(听别人炫耀你没吃到的丰盛晚餐或没看过的电影,有什么意思呢?)
但传统的数学教学却总是这样:“反正有个比你聪明的家伙已经思考清楚了这个问题,你给我记住他们的发现就好了!”
这太无趣了,还是让人们自己去尝试吧。还拿“旋转”打比方,如果转一下会怎样呢?
那转两下呢?转四下呢?
通俗解释:用你自己的语言
当你认真体验完,应该会有想去描述它的冲动:
- 虚数似乎都指向北方,我们可以通过一次瞬时针旋转得到它们
- 噢!我猜通过反向旋转,它们也能指向南方,
- 两次旋转好像会指向相反方向
- 四次旋转后就能重新转回起点
以上都是正确的结论,只是没用数学的语言来描述。但你完全可以使用通俗语言进行推论!
技术细节: 学习正式规范
最后一步是将我们的个人理解转化成规范的记号。这好比分享一首你编写的曲子:你可以哼给自己听,但要写成谱子才能让别人使用。
数学正是我们用来分享思想的曲谱。以下是“虚数”正规的术语:
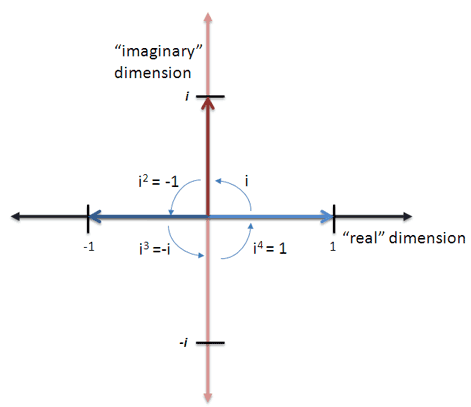
- 我们用小写 i 表示虚轴上的一个单位
- 乘以 i 表示瞬时针 90 度旋转,从而朝“上”;乘以 -i 则指向“南”
- 从 1.0 开始旋转四次会回到起点是正确的:
两次旋转得到负数也是:
进一步可以简化为:
换句话说,i 是 -1 的“一半”。
有点感觉啦?仅仅说出 “i 是 -1 的平方根” 并不够。它没有解释,只是宣称。你没有进行任何体验,也不能获得任何内化的知识。
作为检查列表
我曾经在掌握技术性描述和课后练习题后就感到满足,而现在再也不会。
聚焦学习法(ADEPT)是一个让我确信掌握了所学概念的检查列表。除非找到了一个连接一切的比喻,否则我不认为自己真正掌握了这个概念。
我通常在以下这些地方查找各个层次的资料:
不幸的是,关于比喻,尤其是数学方面,网络上没有很多合适的资源。因此你只能靠自己了。
改变学习的顺序
让事实按顺序展现出来,就像在电脑上传输数据,听上去很符合逻辑。但是谁真正是这样学习的呢?
我一直倾向于使用“从模糊到清晰”的方法进行教学:

从一个粗糙的比喻开始,逐渐磨砺它直到你揭开技术上的细节。
有时候,你需要靠自己弄清技术细节,所以要时刻准备着后退回比喻重新开始:
- 你能用自己的语言解释它们吗?
- 你能解决一个案例问题,用你自己的语言描述每一个步骤吗?
- 你能制作一张图表,展示你怎么理解这个概念的吗?
- 你能把这个概念,关联上你已有的知识吗?
从初始的比喻开始,逐渐增加新的细节和案例,看看自己对以上问题的回答是否仍能成立。
老实说,我们必须承认自己通常会忘记一堂课程 95% 的内容。什么留下来了?一个形象的比喻或图表。
一年后你可能已经忘记了“虚数”的概念,但回想起有关”旋转”的比喻,你会很快回忆起一切。
我们的目标:找到真正可行的解释
我本想找到一个更容易被记住的缩写,但 ADEPT 已经包含了我内化新概念时的所有方法。让我们直面这些问题,不要害羞:仅仅罗列事实能让你学会吗?你还需要什么其他要素呢?我只有一个软乎乎、湿漉漉的大脑,它需要连接用的胶水,而不仅仅是数据。