继续是《数据结构算法与应用:C++语言描述》,第四章数组和矩阵的笔记。本小节介绍稀疏矩阵的内容。这也是本章节最后一节内容。
基本概念
如果一个$m\times n$矩阵中有”许多”元素为0,则称该矩阵为稀疏矩阵(sparse)
对应的非稀疏的矩阵称为稠密矩阵(dense)。而实际上,稀疏矩阵和稠密矩阵之间并没有一个精确的界限。
$n\times n$的对角矩阵和三对角矩阵都是稀疏矩阵,二者都有$O(n)$个非0元素和$O(n^2)$个0元素。而对于一个$n\times n$的三角矩阵,它至少有$\frac{n(n-1)}{2}$个0元素,最多有$\frac{n(n+1)}{2}$个非0元素。在本节中,我们规定一个矩阵是稀疏矩阵,则其非0元素的数目应小于$n^2/3$,有些情况下应小于$n^2/5$,因此可以将三角矩阵视为稠密矩阵。
诸如对角矩阵和三对角矩阵这样的稀疏矩阵,其非0区域的结构很有规律,因此可以设计一个很简单的存储结构,该存储结构的大小就等于矩阵非0区域的大小,本小节主要考察具有不规则非0区域的稀疏矩阵。
数组描述
对于下图a中的$4\times 8$矩阵可以按行主次序把非0元素映射到一维数组中,可到到:2,1,6,7,3,9,8,4,5。
为了重建矩阵结构,必须记录每个非0元素所在的行号和列号,所以在把稀疏矩阵的非0元素映射到数组中时必须提供三个域:row(矩阵元素所在的行号)、col(矩阵元素所在列号)和value(矩阵元素的值)。为此定义了下列所示的模板类Term:
template
class Term{
int row, col;
T value;
};如果a是一个类型为Term的数组,那么下图a中的稀疏矩阵按行主次序存储到a中所得的结果就如图b所示。 
除了存储数组a以外,还必须存储矩阵行数、矩阵列数和非0项的数目。所以存储上图a中的九个非0元素所需要的存储器字节数是21sizeof(int)+9sizeof(T),这里每个非0元素都有两个int类型的行号和列号,然后加上总的矩阵行数,列数以及非0数目。
类SparseMatrix
可以定义一个类SparseMatrix,如下所示,用来把稀疏矩阵按行主次序映射到一维数组中。在定义共享成员时,没有定义加法操作符+,因为它会创建一个临时结果,这个临时结果必须复制到所返回的环境才可以使用。由于SparseMatrix的复制构造函数将会复制每一个元素,因此操作符+中的复制代价太大,这里使用Add函数来避免这种情况的发生。
template
class SparseMatrix{
private:
void Append(const Term& t);
int rows, cols;
// 非0元素的数目
int terms;
// 存储非0元素的数组
Term *a;
// 数组a的大小
int MaxTerms;
public:
SparseMatrix(int maxTerms = 0);
~SparseMatrix(){ delete[] a; }
void Transpose(SparseMatrix& b) const;
void Add(const SparseMatrix &b, SparseMatrix&c)const;
friend std::ostream& operator<<(std::ostream&, const="" sparsematrix&);
friend std::istream& operator>>(std::istream&, SparseMatrix&);
};下面给出构造函数,以及输入操作符和输出操作符,两者的时间复杂性都是$\theta(terms)$。
template
SparseMatrix::SparseMatrix(int maxTerms){
if (maxTerms < 1)
throw BadInitializers();
MaxTerms = maxTerms;
a = new Term[maxTerms];
terms = rows = cols = 0;
}
// 重载<<
template
std::ostream& operator<<(std::ostream& out,="" const="" sparsematrix& x){
// 输出矩阵的特征
out << "rows = " << x.rows << " columns = " << x.rows << std::endl;
out << "nonzeros terms = " << x.terms << std::endl;
// 输出非0元素,每行1个
for (int i = 0; i < x.terms; i++)
out << "a(" << x.a[i].row << ", " << x.a[i].col << ") = " << x.a[i].value << std::endl;
return out;
}
// 重载>>
template
std::istream& operator>>(std::istream& in, SparseMatrix& x){
// 输入矩阵的特征
std::cout << "Enter number of rows, columns, and terms\n";
in >> x.rows >> x.cols >> x.terms;
if (x.terms > x.MaxTerms)
throw NoMem();
// 输入矩阵元素
for (int i = 0; i < x.terms; i++){
cout << "Enter row, column, and value of term " << (i + 1) << std::endl;
in >> x.a[i].row >> x.a[i].col >> x.a[i].value;
}
return in;
}这里在重载输入操作符>>的时候,如果输入的元素数目大于数组a的大小,则会引发一个异常。一种处理异常的方法是删除数组a,然后使用new重新分配一个更大的数组。
矩阵转置
下面程序给出函数Tranpose的代码实现。转置后的矩阵被返回到b中。 首先验证b中是否有足够的空间来存储被转置矩阵的非0元素。如果空间不足,要么重新分配一个更大的数组b.a,要么引发一个异常。在下面的程序中是选择引发异常。如果b中有足够的空间来容纳转置矩阵,则创建两个数组ColSize和RowNext。其中ColSize[i]是指矩阵第i列中的非0元素的数目,而RowNext[i]则是代表转置矩阵第i行的下一个非0元素在b中的位置。
template
void SparseMatrix::Transpose(SparseMatrix& b)const{
// 把*this的转置结果送入b中
// 验证b有足够空间
if (terms > b.MaxTerms)
throw NoMem();
// 设置转置特征
b.cols = rows;
b.rows = cols;
b.terms = terms;
// 初始化
int *ColSize, *RowNext;
ColSize = new int[cols + 1];
RowNext = new int[rows + 1];
for (int i = 1; i 函数Tranpose的时间复杂性是$O(cols+terms)$
矩阵相加
在两个矩阵相加中使用了函数Append,它把一个非0项添加到一个稀疏矩阵的非0项数组的尾部,其时间复杂性是$\theta(1)$。实现代码如下,然后就是两个矩阵相加的实现函数Add,使用两个游标,分别是*this和矩阵b的游标,通过一个while循环来实现相加。
template
void SparseMatrix::Append(const Term& t){
// 把一个非0元素t添加到 *this之中
if (terms >= MaxTerms)
throw NoMem();
a[terms] = t;
terms++;
}
template
void SparseMatrix::Add(const SparseMatrix& b, SparseMatrix& c)const{
// 计算 c = (*this) + b
// 验证可行性
if (rows != b.rows || cols != b.cols)
throw SizeMismatch();
// 设置结果矩阵c的特征
c.rows = rows;
c.cols = cols;
c.terms = 0;
// 定义*this 和b 的游标
int ct = 0, cb = 0;
while (ct < terms && cb < b.terms){
// 每一个元素的行主索引
int indt = a[ct].row * cols + a[ct].col;
int indb = b.a[cb].row * cols + b.a[cb].col;
if (indt < indb){
// b的元素在后面
c.Append(a[ct]);
ct++;
}
else{
if (indt == indb){
// 位置相同
if (a[ct].value + b.a[cb].value){
// 仅当和不为0时,才添加到c中
Term t;
t.row = a[ct].row;
t.col = a[ct].col;
t.value = a[ct].value + b.a[cb].value;
c.Append(t);
}
ct++;
cb++;
}
else{
// b的元素在前面
c.Append(b.a[cb]);
cb++;
}
}
}
// 复制剩余元素
for (; ct < terms; ct++)
c.Append(a[ct]);
for (; cb < b.terms; cb++)
c.Append(b.a[cb]);
}函数Add的时间复杂性是$O(terms+b.terms)$。而如果用二维数组来描述每个矩阵,则两个矩阵相加耗时$O(rowscols)$,当terms+b.terms远小于**rowscols**时,稀疏矩阵的加法执行效率将大大提高。
链表描述
用一维数组来描述稀疏矩阵所存在的缺点是:当我们创建这个一维数组时,必须知道稀疏矩阵中的非0元素总数。 在我们自定义的类SparseMatrix中,当实际非0元素数目多于估计的初始化一维数组时设定的非0元素数目时,会引发一个异常。还有一种做法是可以分配一个更大的、新的数组,然后复制元素,并删除老的数组,但是这种做法会使得算法效率降低,并且也同样需要估计新数组需要多大的问题。
因此,这里就如同线性表一样,除了使用数组描述,还有基于指针的描述,也就是链表描述。
描述
链表描述的一种可行方案是把每行的非0元素串接在一起,构成一个链表,如下图所示。
图中每个非阴影节点代表稀疏矩阵中的一个非0元素,它有三个域:col(非0元素所在列号)、value(非0元素的值)和link(指向下一个非阴影节点的指针)。仅当矩阵某行中至少包含一个非0元素才会为该行创建一个链表。在行链表中,每个节点按其col值得升序进行排序。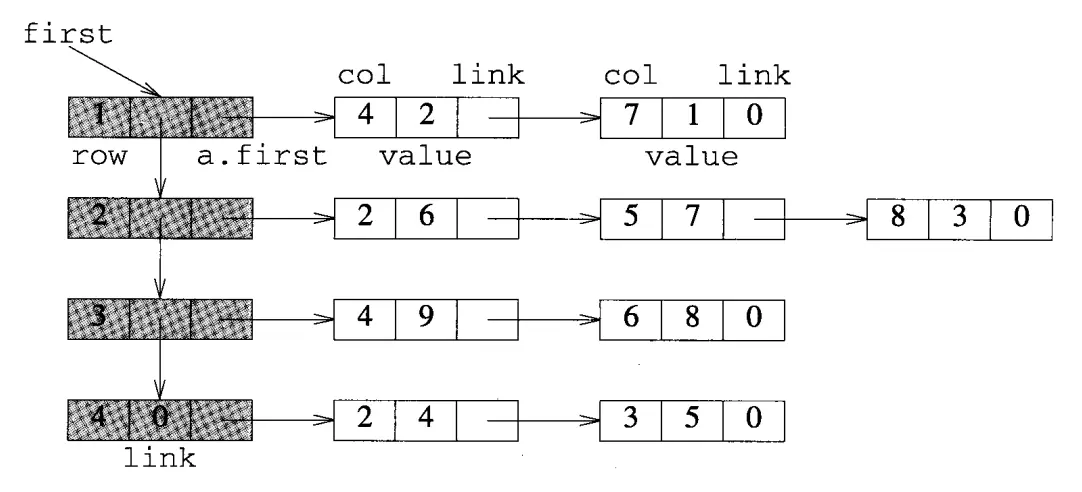
然后再用一个链表将所有的行链表,即图中阴影链表收集在一起。各个阴影节点按其row值得升序排列,每个阴影节点可以被视为一个行链表的头节点,因此阴影链表可以被视为头节点链表。
链表节点类型
这里分别定义图中非阴影节点CNode和阴影节点HeadNode,其代码实现如下:
#ifndef LINKMATRIX_H_
#define LINKMATRIX_H_
#include
#include"ChainList.h"
template
class CNode{
private:
int col;
T value;
public:
int operator!=(const CNode& y){
return (value != y.value);
}
void Output(std::ostream& out)const{
out << "column = " << col << ", value= " << value;
}
};
template
std::ostream& operator<<(std::ostream& out,="" const="" cnode& x){
x.Output(out);
out << std::endl;
return out;
}
template
class HeadNode{
private:
int row;
// 行链表
Chain> a;
public:
int operator!=(const HeadNode& y){
return (row != y.row);
}
void Output(std::ostream& out)const{
out << "row = " << row;
}
};
template
std::ostream& operator<<(std::ostream& out,="" const="" headnode& x){
x.Output(out);
out << std::endl;
return out;
}
#endif接下来就是定义类LinkMatrix,如下所示。
template
class LinkMatrix{
private:
int rows, cols;
// 头节点链表
Chain> a;
public:
LinkMatrix(){}
~LinkMatrix(){}
void Transpose(LinkMatrix& b)const;
void Add(const LinkMatrix& b, LinkMatrix& c)const;
template
friend std::ostream& operator<<(std::ostream&, const="" linkmatrix&);
template
friend std::istream& operator>>(std::istream&, const LinkMatrix&);
};重载>>
重载输入操作符>>。首先是要求输入矩阵的维数以及非0元素的个数。然后输入各个非0元素并把它们收集到各行链表中。用变量H代表当前行链表的头节点,如果下一个非0元素不属于当前行链表,则将当前行链表添加到矩阵x的头节点x.a之中;接下来,H被设置为指向一个新的行链表,同时将刚才那个非0元素添加到这个新的行链表之中。如果新的非0元素属于当前行链表,则只需要简单地把它添加到链表H.a中
template
std::istream& operator>>(std::istream& in, const LinkMatrix& x){
// 从输入流中输入矩阵x
// 删除x中所有节点
x.a.Erase();
// 获取矩阵特征
int terms; // 输入的元素数
cout << "Enter numbers of rows, columns, and terms\n";
in >> x.rows >> x.cols >> terms;
// 虚设第0行
HeadNode H; // 当前行的头节点
H.row = 0; // 当前行号
// 输入x的非0元素
for (int i = 1; i <= terms;="" i++){="" 输入下一个元素="" cout="" <<="" "enter="" row,="" column,="" and="" value="" of="" term="" "="" i="" std::endl;="" int="" col;="" t="" value;="" in="">> row >> col >> value;
// 检查新元素是否属于当前行
if (row > H.row){
// 如果不是第0行,则把当前行的头节点H 添加到头节点链表x.a之中
if (H.row)
x.a.Append(H);
// 为新的一行准备H
H.row = row;
// 置链表头指针first=0
H.a.Zero();
}
// 添加新元素
CNode *c = new CNode;
c->col = col;
c->value = value;
H.a.Append(*c);
}
// 注意矩阵的最后一行
if (H.row)
x.a.Append(H);
H.a.Zero();
return in;
}重载<<
这里为了输出链表表示的稀疏矩阵,使用了一个链表遍历器依次检查头节点链表中的每个节点。代码的时间复杂性与非0元素的数目呈正比。
template
std::ostream& operator<<(std::ostream& out,="" const="" linkmatrix& x){
// 把矩阵x送至输出流
ChainIterator> p; // 头节点遍历器
// 输出矩阵的维数
out << "rows = " << x.rows << ",columns = " << x.cols << std::endl;
// 将h指向第一个头节点
HeadNode *h = p.Initialize(x.a);
if (!h){
out << "No non-zero terms\n";
return out;
}
// 每次输出一行
while (h){
out << "row = " << h->row << std::endl;
out << h->a << "\n"; // 输出行链表;
// 下一个头节点
h = p.Next();
}
return out;
}函数Tranpose
对于转置操作,可以采用箱子来从矩阵this中收集位于同一行的非0元素。*bin[i]是结果矩阵b中第i行非0元素所对应的链表。其实现如下所示
template
void LinkMatrix::Transpose(LinkMatrix& b)const{
// 转置 *this,并把结果放入b
b.a.Erase();
// 创建用来收集b中各行元素的箱子
Chain> *bin;
bin = new Chain>[cols + 1];
// 头节点遍历器
ChainIterator> p;
// h 指向*this的第一个头节点
HeadNode *h = p.Initialize(a);
// 把*this的元素复制到箱子中
while (h){
int r = h->row;
// 行链表遍历器
ChainIterator> q;
// 将z指向行链表的第一个节点
CNode *z = q.Initialize(h->a);
// 临时节点
CNode x;
// *this第r行中的元素变成b中第r列的元素
x.col = r;
// 检查*this第r行的所有非0元素
while (z){
x.value = z->value;
bin[z->col].Append(x);
z = q.Next();
}
h = p.Next();
}
// 设置b的维数
b.rows = cols;
b.cols = rows;
// 装配b的头节点链表
HeadNode H;
// 搜索箱子
for (int i = 1; i 其中while循环所需要的时间与非0元素的数目呈线性关系,for循环所需要的时间则与输入矩阵的列数呈线性关系,因此总的时间与这两个量的和呈线性关系。
小结
到这里,第四章数组和矩阵的内容就结束了。本小节主要介绍稀疏矩阵的内容,暂时来说,对于数组描述的掌握是要更好于链表描述的,还需要好好琢磨琢磨,研究一下。