正态分布随机数的生成 (2)接着上一次讲的逆变换和 Box-Muller 方法，这次我们来谈谈接受—拒绝法和非常快的 Z

接受—拒绝法

求反变换固然还可行，但是碰到无法解析求逆的函数，用数值方法总归比较慢。下面我们就来说说另一个能够适合任何概率密度分布的方法——接受—拒绝法 (Acceptance-Rejection Method)，国内也有翻译成叫做舍选法的。接受—拒绝法的思路其实很简单——比如说你想要正态分布，我们就弄个方框框把它框起来，然后均匀地往里面扔飞镖。扔到曲线以下我就留着，扔到曲线以上就不要了。这样搞好以后来看，曲线之下的点就是（二维）均匀分布的。那这些点的横坐标就正好满足我们要的分布——高的地方的点就多，低的地方的点就少嘛。

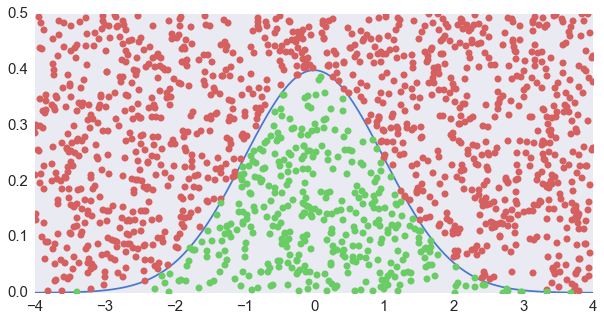
accept-rejection

很直观是吧？更普遍来讲，如果要生成一个概率密度为 f(x) 的分布，我们可以

先找到一个容易抽样的辅助分布 g(x)（也就是框框，不一定是均匀分布啦），使得存在一个常数 M>1，在整个 x 的定义域上都有 f(x)≤Mg(x)。
生成符合 g(x) 分布的随机数 x。
生成一个在 (0,1) 上均匀分布的随机数 u。
看看是不是满足 u<f(x)/Mg(x)。如果满足就保留 x，否则就丢弃。于是得到的 x 就符合 f(x) 分布。

实际上就是生成一堆 x 轴均匀分布，y 轴在 Mg(x) 之内的点，然后仅保留 f(x) 曲线下的那部分，就和我们看到的这个图是一个意思。

要比较严格的证明的话，我们先看看在操作中接受数据点 x 的概率。由于 u 是均匀分布的，所以接受概率

P (accept) = P (U < f ( X ) M g ( X )) = 𝔼 [f ( X ) M g ( X )] = \int f ( X ) M g ( X ) g (x) d x = 1 M \int f (x) d x = 1 M

也就是说能够保留数据点的概率是

1/M。那么利用贝叶斯法则，在接受条件下得到的分布

g (x | accept) = P ( accept | X = x ) g ( x ) P ( accept ) = f ( x ) M g ( x ) g ( x ) 1 / M = f (x)

这东西看起来很美很方便啊，但是请注意，所有的抽样中，被接受的概率只有

1/M，意味着如果

M 很大，就有大量的采样被浪费掉了。特别是像正态分布这种尾巴很长的……要是直接用方框框的话，得浪费多少采样才能遇上一个在

5σ 之外的啊。为了改进算法的效率，就需要让

g(x) 尽量能够贴近

f(x)，于是就有了这个神奇的金字塔 (Ziggurat) 方法。

Ziggurat 方法

Ziggurat 方法的思路其实也很直观，就是要让 g(x) 尽量贴近 f(x)。怎么贴近呢？就像这样：

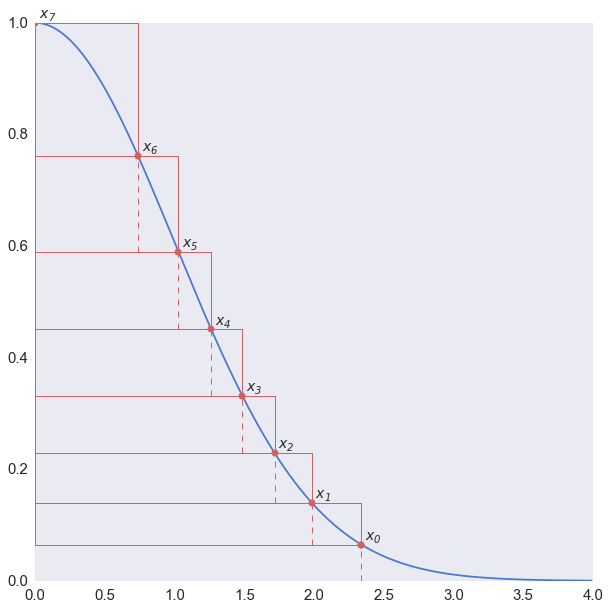
ziggurat

是不是像一个有阶梯的金字塔？Ziggurat 这个词最初是说苏美尔人建的金字塔，但是其实玛雅人造的那个奇琴伊察的金字塔看起来也差不多……我前两年去的时候还画了一幅画就像这样

跑题了……为了计算方便起见，我们生成的是 e−x2/2 而不是原始的正态分布。首先把图形分成好多个（一般实际中用 128 个或 256 个）阶梯一样的长方块，每个长方块的面积都是相等的，并且还和最下面的带长长的尾巴的这一条的面积相等。这些点的位置……只能靠逼近的方法了。习惯上把 x0 的位置叫做参数 r，那最下面一块的面积 v 就是虚线左边的长方形面积加上尾巴：

v = r \cdot f (r) + \int \infty r f (x) d x

先假定一个 r 值，求出 v 后逐个求到最上面一个 xn−1 的位置，如果最上面一块面积不是 v 再调整 r 直到各块面积相等。好在 r 一旦算好了就可以写成一个参数，用不着每次都去重新算。甚至所有这些分划点也可以直接写成数据表，用的时候直接查表就行了。

这些块块分好了以后怎么办呢？先不考虑尾巴，它是这样操作的：

随机选定一层 0≤i<n；
产生一个 [0,1] 的均匀分布的随机数 U0，令 x=U0xi，也就是随机产生一个均匀分布在实线框中的 x 值。
如果 x<xi+1，也就是落在虚线框内，那肯定就在图形之内啦，直接返回 x。
否则，那就是落在虚线和实现之间的部分，必须要做个判定了。在这个小框框中随机产生一个 y，即先产生一个均匀分布的 U1，令 y=yi+U1(yi+1−yi)。
如果 y<f(x)，返回 x。否则就重新来过。

要是正好选到了尾巴怎么办呢？算法用了一个技巧，它用指数函数来逼近这个尾巴，生成 x=−ln(U0)/r，y=−ln(U1)，只要 2y>x2 就可以返回 x+r。

这个方法好就好在，分块的多少只影响速度，不影响精度——因为在每一块中都是经过接受—拒绝的，所以生成的是精确的正态分布，哪怕只用这 8 块也可以。随着分块增多，金字塔越来越贴合目标函数，做检验被拒绝的概率也大大降低了。

原始代码可以看这里，基本思路就是上面说的这些，程序里面用了 SHR3 随机数生成器来生成均匀分布的 32 位整数，把所有需要用于比较的分划点都算好后存起来，并且用了一些位操作来提高效率。我把它移植到了 Python 上，配合 NumPy 使用，可以去 GitHub 上下载，或者直接 pip install zignor 就可以啦！

来看下速度

import zignor import scipy.stats as stats N = 10**7 %time x = zignor.randn(N) stats.normaltest(x)

import zignor

import scipy.stats as stats

N = 10**7

%time x = zignor.randn(N)

stats.normaltest(x)

Wall time: 93.1 ms
NormaltestResult(statistic=1.1365384917237324, pvalue=0.56650507170017939)

比 Box-Muller 变换快了四倍呢！哇咔咔咔~

参考资料

G. Marsaglia and W.W. Tsang: The Ziggurat Method for Generating Random Variables. Journal of Statistical Software, vol. 5, no. 8, pp. 1–7, 2000.
Doornik, J.A. (2005), “An Improved Ziggurat Method to Generate Normal Random Samples”, mimeo, Nuffield College, University of Oxford.

更多算法内容请见《算法拾珠》。