正态分布随机数的生成正态分布——听起来非常耳熟，用起来也很顺手——因为很多语言都已经内置了有关正态分布的各种工具。但其实

正态分布——听起来非常耳熟，用起来也很顺手——因为很多语言都已经内置了有关正态分布的各种工具。但其实，在这个最普遍、最广泛的正态分布背后，要生成它还有很多学问呢。

f (x | μ, σ) = 1 σ 2 π ‾ ‾ ‾ \sqrt e - ( x - μ ) 2 2 σ 2

难道教科书上没有讲吗？看看概率书上是怎么说的……比如我手头这本浙大版的《概率论与数理统计》（第四版）第 378 页上说……“标准正态变量的分布函数 Φ(x) 的反函数不存在显式，故不能用逆变换法产生标准正态变量……”

反变换法

等下！反函数不存在显式……这都什么年代了，没有解析解难道不能用数值解嘛！求百分位这么常见的动作，怎么会不能做呢？Excel 里面提供了 NORMINV 函数，R 语言里面有 qnorm，在 Python 里面可以用 SciPy.stats 里提供的 norm.ppf：

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
N = 10 ** 7
%time x = stats.norm.ppf(np.random.rand(N, 1))
plt.hist(x, 50)

Wall time: 1.58 s

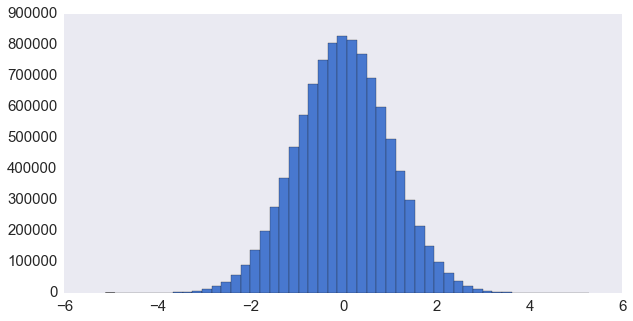
normal_inversetf

当然……不算快啦，但还是可以用的。这个给高斯积分求逆的实现可以看 SciPy 的 ndtri() 函数。这段代码来自于 Cephes 数学库，采用了分段近似的方法但是精度还相当不错——明明是 80 年代末就有了！

这个变换很直观啦，如果你再想变回均匀分布，只要再用一次分布函数就好了：

x = stats.norm.cdf(x)

中心极限定理……还是不要用的好

那教科书上教的是什么方法呢？它祭出了中心极限定理…… 取 n 个相互独立的均匀分布 Xi=U(0,1)，E(Xi)=12，Var(Xi)=112，那么根据中心极限定理，n 比较大的时候近似有

Z = \sum i = 1 n X i - E ( \sum i = 1 n X i ) V a r ( \sum i = 1 n X i ) ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾  ⎷   = \sum i = 1 n X i - n 2 n ‾ \sqrt 1 12 ‾ ‾ ‾ \sqrt \sim N (0, 1) .

取 n=12 则近似有

Z = \sum i = 1 12 U i - 6 \sim N (0, 1) .

这个呢……我们也来试试看。

%time g = np.sum(np.random.rand(N, 12), 1) - 6
plt.hist(g, 50)

Wall time: 2.55 s

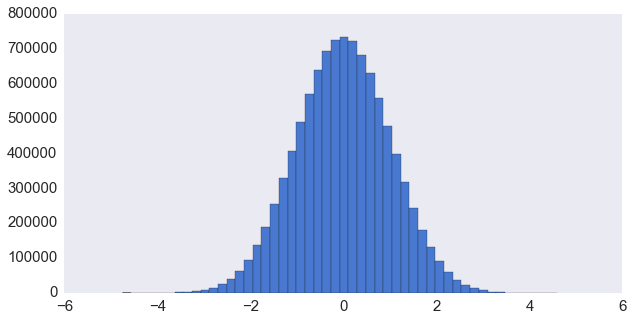
normal_clt

更慢了。形状倒是有那么点意思。那我们来看看它生成的质量如何：

stats.normaltest(g)

NormaltestResult(statistic=4785.7373110266581, pvalue=0.0)

竟然可耻地毫无争议地失败了…… (╯‵□′)╯︵┻━┻ 我们的样本数比较大（107），用仅仅 12 个做平均是很难得到合理的“正态”样本的。可要是取更大的 n 的话，要生成太多的随机数又实在太慢了。如果需要的样本数少一点（比如 1000 个）倒还可以勉强凑合：

stats.normaltest(np.sum(np.random.rand(1000, 12), 1) - 6)

NormaltestResult(statistic=1.8167274769305835, pvalue=0.40318339808171011)

好吧，这方法大概只有理论上的意义……我们来看一个比较常用的实际方法是怎么做的：

Box-Muller 变换

我们再来看看这个反变换的事。基本上我们的问题就是要计算

I = \int \infty - \infty e - x 2 2 d x

大家都知道这个积分没有初等函数的表示。不过呢

I 2 = \int \infty - \infty e - x 2 2 d x \int \infty - \infty e - y 2 2 d y = \int \infty - \infty \int \infty - \infty e - x 2 + y 2 2 d x d y

注意看右边，这个形式让我们想到了……极坐标！令 x=rcosθ，y=rsinθ，那么 dxdy 变成 drdθ 的时候要记得乘上雅各比矩阵：

d x d y = ∣ ∣ ∣ ∣ \partial x \partial r \partial y \partial r \partial x \partial θ \partial y \partial θ ∣ ∣ ∣ ∣ d r d θ = r d r d θ

于是

I 2 = \int \infty r = 0 \int 2 π θ = 0 e - r 2 2 r d r d θ = 2 π \int \infty r = 0 e - r 2 2 r d r = 2 π \int \infty r = 0 e - r 2 2 d (r 2 2) = 2 π

有了这个技巧就求出了积分。如果再把反变换方法应用到这里，Θ 可以均匀地取 [0,2π] 中的值，即

Θ = 2 π U 1

还可以同理计算出

ℙ (R \leq r) = \int r r' = 0 e - r ' 2 2 r' d r' = 1 - e - r 2 / 2

令其满足均匀分布 1−U2，则

R = - 2 ln (U 2) ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ \sqrt

因此，只需要产生均匀分布 U1 和 U2，就可以计算 R 和 Θ，进而计算出 X 和 Y 两个相互独立的正态分布了。

Python 里面的 random.gauss() 函数用的就是这样一个实现。我们来试试看：

%time x = [random.gauss(0, 1) for _ in range(N)]

Wall time: 10.4 s

当然……不是很快。不但是因为 Python 本身的速度，更是因为要计算好多次三角函数。NumPy 里面的 numpy.random.randn() 对此又做了进一步的优化。代码可以见 rk_gauss() 函数。它的原理是这样的：我们要的分布是

X Y = R cos (Θ) = - 2 ln U 1 ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ \sqrt cos (2 π U 2) = R sin (Θ) = - 2 ln U 1 ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ \sqrt sin (2 π U 2)

如果我们产生两个独立的均匀分布 U1 和 U2，并且抛弃单位圆之外的点，那么 s=U21+U22 也是均匀分布的。为什么呢？因为

f U 1, U 2 (u, v) = 1 π

将坐标代换为 r 和 θ，乘上一个雅各比行列式，我们前面算过了这个行列式就等于 r，所以：

f R, Θ (r, θ) = r π

Θ 是均匀分布在 [0,2π) 上的，所以

f R (r) = \int 2 π 0 f R, Θ (r, θ) d θ = 2 r

再做一次变量代换

f R 2 (s) = f R (r) d r d ( r 2 ) = 2 r \cdot 1 2 r = 1

好了，既然 s 也是均匀分布的，那么 −2lnU1‾‾‾‾‾‾‾‾√ 和 −2lns‾‾‾‾‾‾‾√ 就是同分布的。而又因为

cos Θ, sin Θ = U 1 R, U 2 R = U 1 s \sqrt, U 2 s \sqrt

那么

u - 2 ln s s ‾ ‾ ‾ ‾ ‾ ‾ ‾ \sqrt, v - 2 ln s s ‾ ‾ ‾ ‾ ‾ ‾ ‾ \sqrt

就是我们要找的两个独立正态分布。

%time x = np.random.randn(N)

Wall time: 363 ms

这速度还是十分不错的（当然一大原因是 NumPy 是 C 实现的）。本来 Box-Muller 包括 Matlab 在内的各大数值软件所采用的标准正态分布生成方法，直到出现了速度更快的金字塔 (Ziggurat) 方法。NumPy 出于兼容旧版本的考虑迟迟没有更新，导致生成随机数的速度已经落在了 Matlab 和 Julia 后面。那么这个神奇的金字塔又是怎么回事呢？我们另开一篇细谈。