前言
此系列是本人对于学习计算机图形学过程中的记录及总结,所看教材是《Fundamentals of Computer Graphics (FOURTH EDITION)》。本文的图片也主要来源此书。以博客作为学习记录,理解之中若有不足还请大佬们指教。
本系列中我跳过了第五章线性代数知识,本篇主要记录第六章Transformation Matrices的学习。
在3D场景中,线性代数有许多的应用。在几何变换中,比如位移、旋转、缩放等等均可以通过矩阵相乘完成。本章节主要讲述线性代数矩阵在几何变换中的作用。
线性代数应用于变换,其本质是矩阵相乘改变基向量。之前学习了3blue1brown的线性代数本质,对线性代数有了更深刻的理解,非常推荐此资源。
6.1 二维线性变换(2D Linear Transformations)
我们可以使用2 * 2矩阵对二维向量进行线性变换(linear transformation),其基本模板如下:
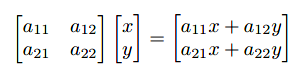
二维场景中笛卡尔积坐标系的基向量为(1, 0)(X轴单位向量),(0, 1)(y轴单位向量)。
下文描述各种变换如何通过矩阵相乘进行实现。
6.1.1缩放(Scaling)
通过矩阵相乘,改变基向量的大小可以实现缩放操作,比如基向量均为原来的两倍,新图像的长宽会各自为原先两倍,面积则扩大四倍。表达式如下:
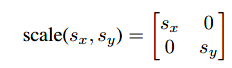
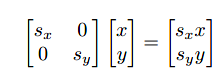
举例:
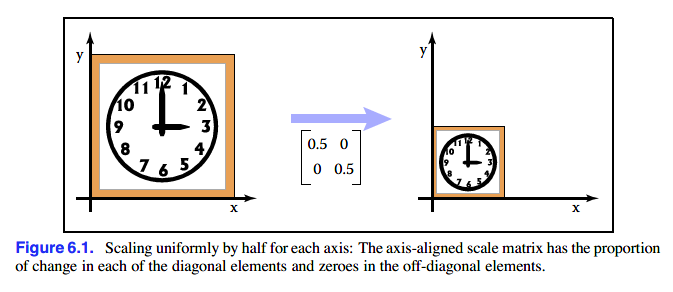
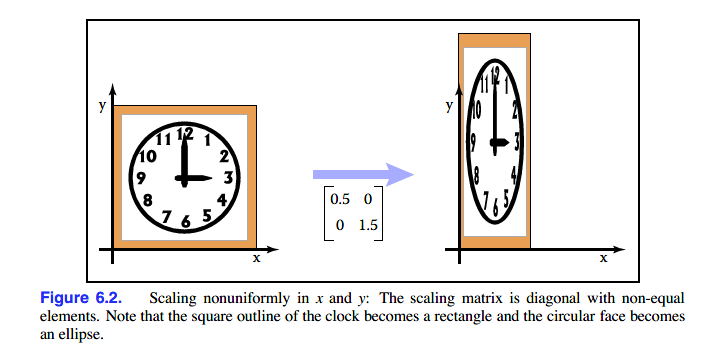
同时,我们可以发现缩放矩阵为对角矩阵
6.1.2错切(Shearing)
错切是一种推移效果,有水平错切与垂直错切的矩阵如下:
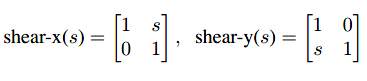
以下举例示范错切效果。
沿水平方向错切:
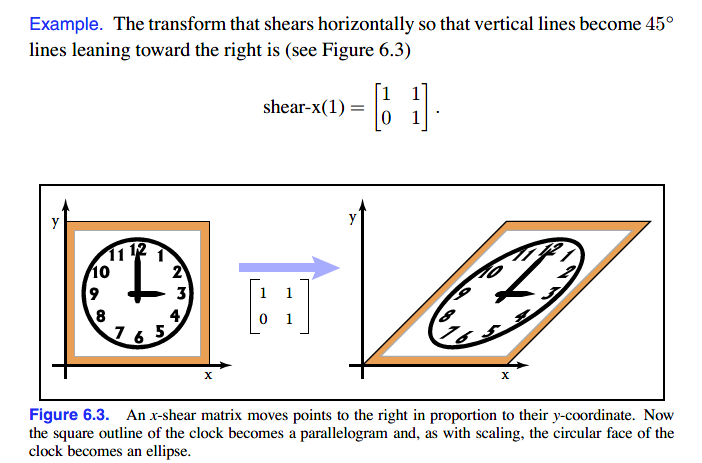
沿垂直方向错切
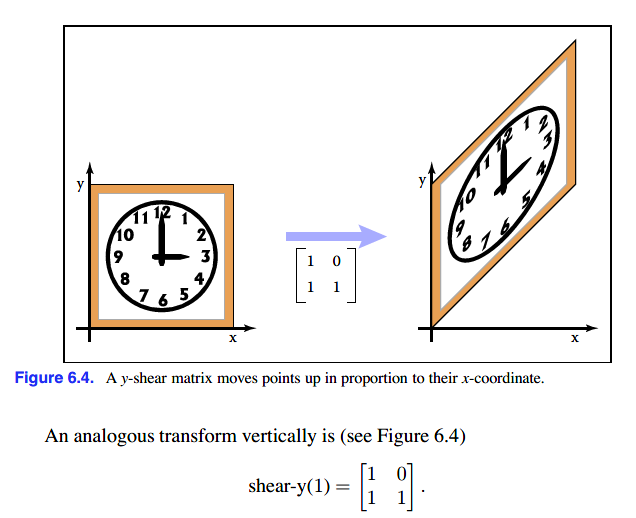
如何计算这一个s值呢?使用tan计算其错切角度即可,举例水平错切:
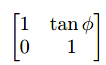
6.1.3旋转(Rotation)
旋转操作本质是通过改变基向量的方向,使得坐标系中的向量方向发生改变,从而形成图像旋转的效果。
先看如何对向量进行方向改变。假设我们有向量a,其与x轴的夹角为α,欲逆时针旋转φ角度至b。
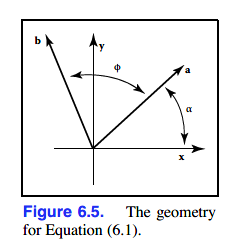
旋转过后向量的长度不会改变,现a的长度为r,于是有:
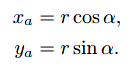
因为逆时针旋转φ后b的长度仍为r,于是有:
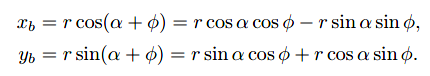
代入a各方向的表达式,于是可得:
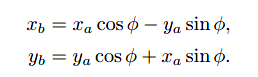
因此,在旋转操作中,我们要把a向量逆时针旋转φ至b向量只需使用如下变换矩阵:
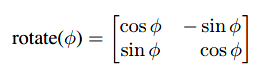
具体使用时钟举例,逆时针旋转45°:
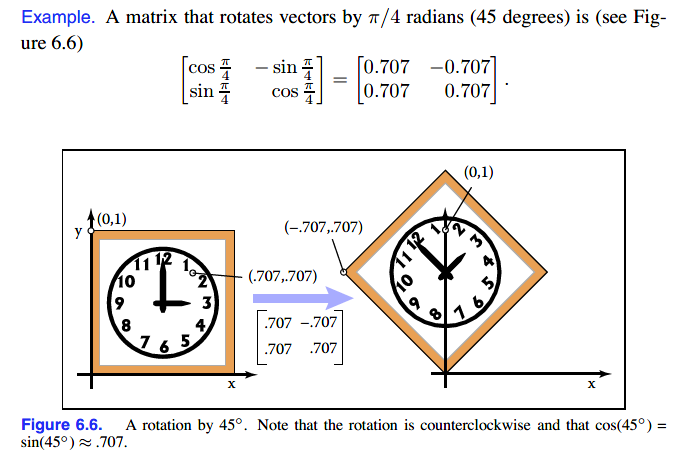
若进行顺时针,只需角度前加负号即可。
同时通过观察公式与计算我们可以发现,旋转矩阵为正交矩阵,这在之后的变换分解会再次提到。
6.1.4反射(Reflection)
吐槽下这个翻译感觉有点奇怪,但解释不奇怪。反射是一个物体变换成它的镜像的映射。
本小节直接列举简单的y轴反射及x轴反射,公式如下:
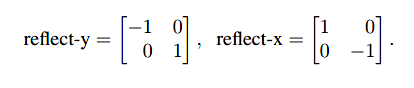
如下为y轴反射效果:
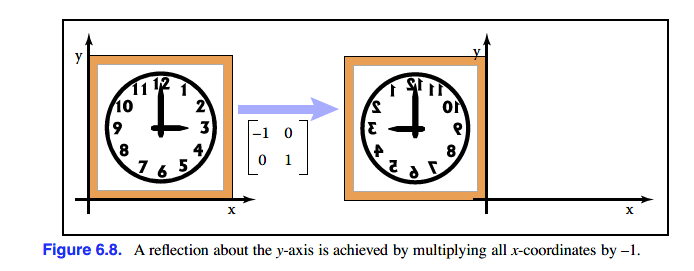
6.1.5变换的组合与分解(Composition and Decomposition of Transformations)
图像程序中往往会有多种变换,比如先缩放,再做旋转:
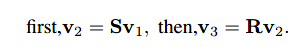
以上等式相当于:
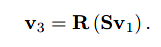
如此,可通过矩阵相乘完成一次性变换:
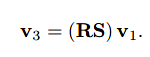
也就是说,我们可以通过M=RS,使用合成M矩阵对图像进行一次线性变换。注意合成矩阵的相乘顺序,比如这里我们先应用S变换,再应用R变换,获得合成矩阵M的顺序为从右往左依次相乘,即M=RS。这部分具体内容涉及线性代数相关的知识。
举例,假设先做缩放,再做旋转。这两个步骤我们可以仅通过一个变换矩阵完成。
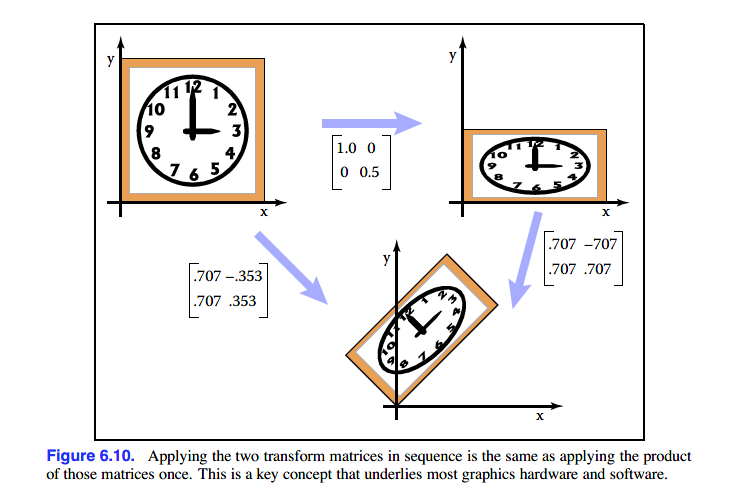
对应的等式计算如下:
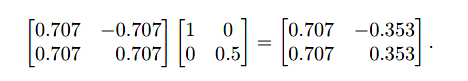
6.1.6变换的分解
了解变换的组合之后,我们可以通过一个合成矩阵直接进行变换。但是有时候在应用之中,直接给出一个合成矩阵,用户希望看见合成矩阵分解出来的几个步骤过程。
本小节讲述几种可矩阵分解的方法
Symmetric Eigenvalue Decomposition(对称矩阵特征值分解?)
先从对称矩阵(symmetric matrix) 开始。对称矩阵可以通过特征值分解分解为以下形式:
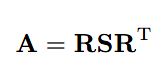
其中R为正交矩阵(orthogonal matrix),S为对角矩阵(diagonal matrix)。我们把R的列(特征向量)称为v1、v2,S矩阵的对角元素(特征值)称为λ1和λ2。
从图形变换的视角,我们可以把R视为旋转矩阵,S视为缩放矩阵,三个变换步骤则对应如下:
- 先旋转v1、v2至x轴与y轴(R的转置矩阵进行变换操作)
- 按照特征值(λ1,λ2)对x、y进行缩放(S矩阵进行变换操作)
- 将x轴与y轴旋转回v1、v2位置(R矩阵进行变换操作)
过程图例如下:
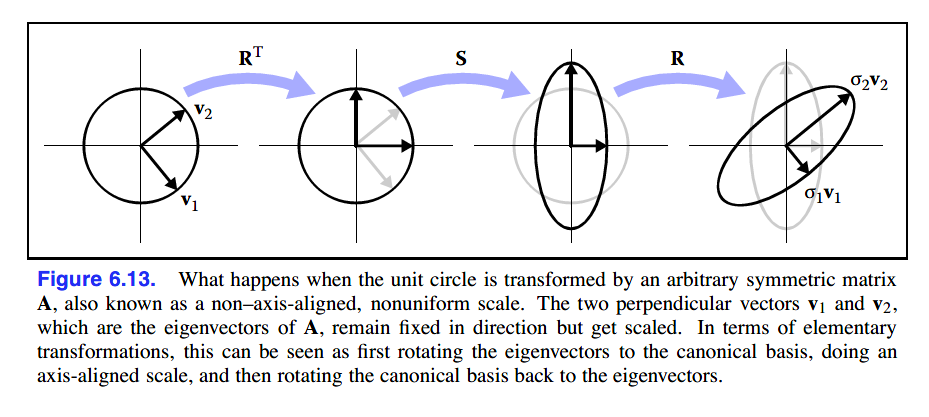
以下我们拿一个对称矩阵进行分解举例,过程中会涉及到线性代数相关的知识。
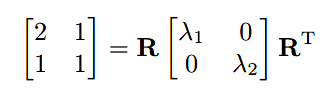


以上为手写过程举例,最后即可得分解结果

Singular Value Decomposition(奇异值分解)
对于非对称矩阵,可以使用奇异值分解(Singular Value Decomposition, SVD)。SVD可以把任何变换分解为旋转、缩放、旋转三个变换矩阵。
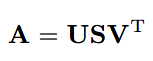
U与V替代了原先的R,它们的列也分别为A的ui(左奇异向量,left singular vectors),vi(右奇异向量,right singular vectors),同时也是不同的正交矩阵。中间S的对称元素也不再是特征值,而是A的奇异值(singular values)。同时,当A为对称矩阵且含有非负特征值时,SVD与特征值分解是相同的。
几个矩阵的变换步骤如下:
- 分别旋转v1、v2至x轴与y轴。(V的转置矩阵进行变换)
- 使用(σ1, σ2)缩放x与y。(S矩阵进行变换)
- 旋转x轴与y轴至u1、u2。(U进行变换)
过程如图例:
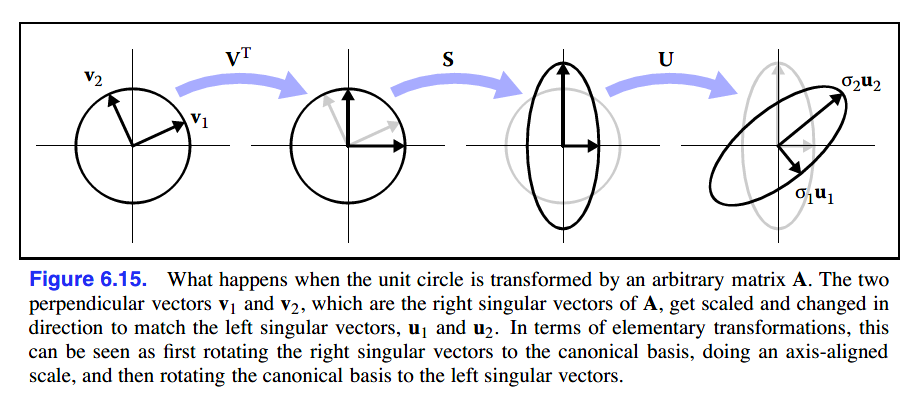
奇异值分解的计算思路是通过矩阵A与A的转置矩阵相乘获得对称矩阵,对对称矩阵进行特征值分解。具体接题过程在知乎上看见一篇非常好的文章——奇异值分解的揭秘(一):矩阵的奇异值分解过程,在此就不赘述了。
书中例子

综上,我们可以发现任何矩阵都可以通过SVD进行分解,分解出来的变换顺序也是旋转、缩放、旋转。
Paeth Decomposition of Rotations
另外一种分解是使用错切来表示非零旋转,由Paeth于1990年提出(/(ㄒoㄒ)/,找不到相关链接)。
公式如下:
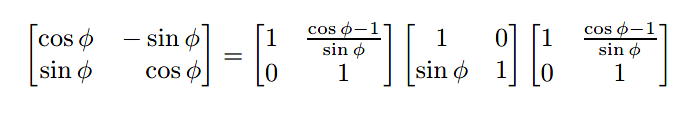
比如旋转45°
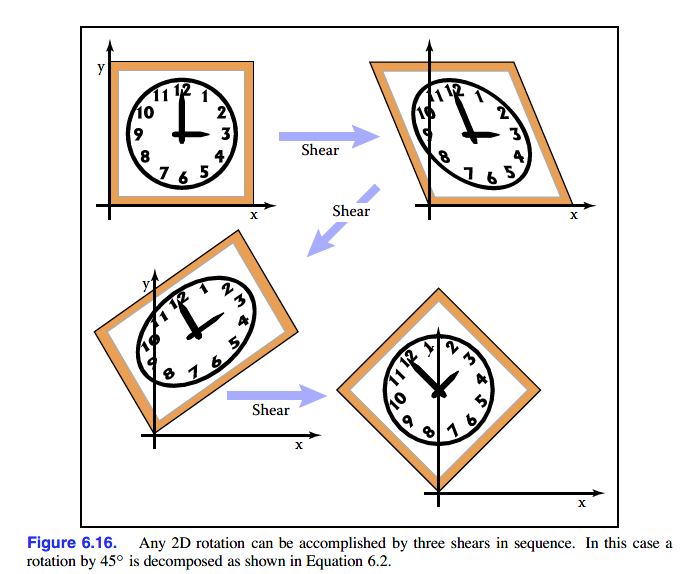
用三次错切完成了旋转效果。
6.2三维线性变换(3D Linear Transformations)
三维的线性变换是对二维线性变换的扩展,有些变换比较类似,有些情况更为复杂。
比如缩放操作较为简单:
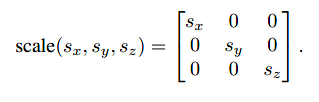
而旋转操作,因为在三维空间中有了更多的旋转轴,因此旋转的情况会更为复杂,以下是三维空间中绕z轴、绕x轴、绕y轴的旋转公式:
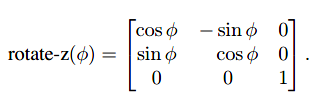
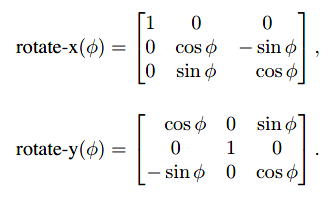
下一小节再涉及任意轴的旋转。
对于错切,也可以沿着某一条特定的轴进行操作:
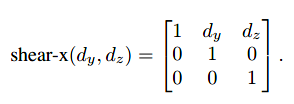
6.2.1任意轴的三维旋转(Arbitrary 3D Rotations)
假设旋转是围绕a向量进行旋转,先对a构建一个坐标系,假设a对应w(对应xyz轴中的z轴),将此坐标系转移至xyz坐标系,此时将物体绕w轴旋转(相当于绕z轴旋转,据此可以用到上文的公式)。旋转完成后,将a对应的坐标系复原即可。
画图表示步骤如下:
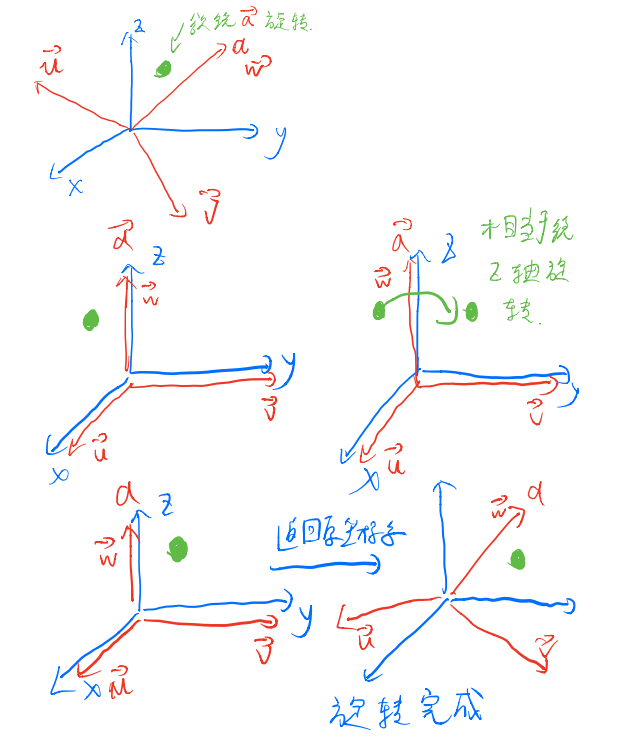
对应公式:
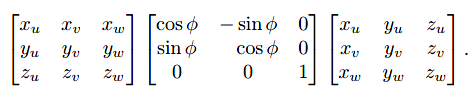
了解此步骤时,除了书上内容也结合了油管的视频Linear Algebra 21i: How to Represent a Rotation with respect to an Arbitrary Axis,理解不到位之处还请大佬指教。
6.2.2变换法向量(Transforming Normal Vectors)
表面法向量(surface normals)垂直于与表面相切的平面。在发生三维线性变换时,这些向量的改变并非那么简单。
举个例子,经过M矩阵的变换后,表面的切向量t仍与表面相切,但表面法向量n可能不再与t垂直,也即不再垂直于表面。据此我们可以使用一个矩阵N,使得变换后的n向量与表面垂直。
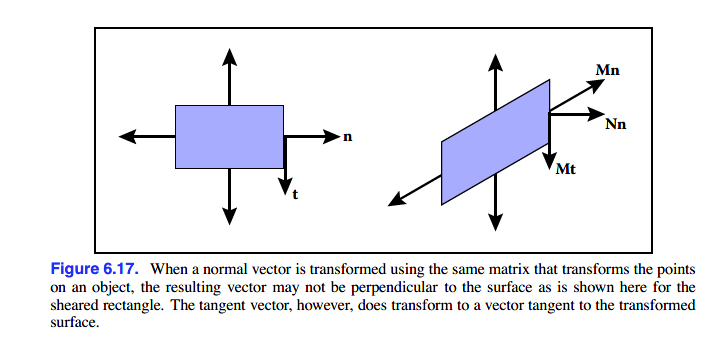
因为切向量是与法向量垂直的,变换后的切向量仍旧与表面相切:
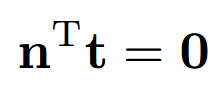
所以可以利用切向量来获得N矩阵:
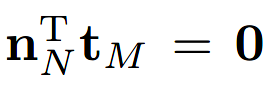
其中,
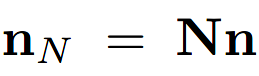
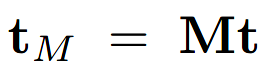
经过一系列的公式变换,可得:
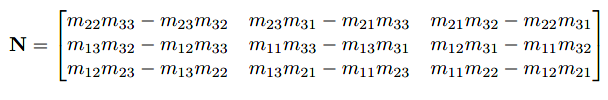
其中mij代表M中相应位置的元素
6.3位移与仿射变换(Translation and Affine Transformations)
以上内容均是用矩阵M进行缩放、错切、旋转、反射的变换,未涉及到位移变换,本小节主要讲述位移变换。
位移变换即是要达到以下效果:
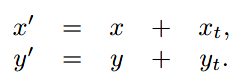
但是2*2矩阵并不能达到此效果,于是可以使用一个巧妙的方法,即:
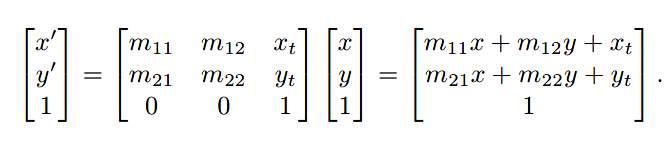
这便是仿射变换(affine transformation),通过*齐次坐标(homogeneous coordinates)*增加一个维度完成位移。
根据上式,仿射变换既可以完成位移,又可以进行上文的缩放、错切旋转等等操作。
“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”—— F.S. Hill, JR。
当我们需要区分点与向量时,同样可以用齐次坐标区分。
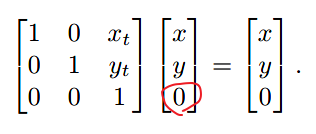
当此第三个维度用0表示时,若从齐次坐标转换至笛卡尔坐标系,x、y值则表示为(x/0, y/0)即为无穷大。
当第三个维度用1表示时,x、y值则表示为(x, y),即为点坐标。
在三维空间中,同理增加一个维度:
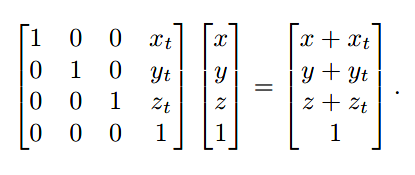
在往后的透视章节中,我们会看到除了0和1外,齐次坐标更多的应用。
6.4变换矩阵的逆矩阵(Inverses of Transformation Matrices)
变换矩阵可以通过其逆矩阵来恢复其原状,对于合成矩阵也是如此。例如:
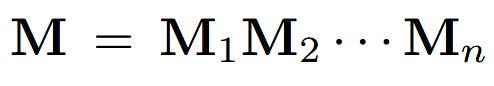
其逆变换为:
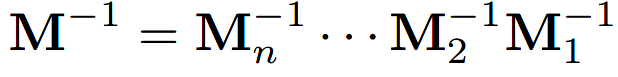
另外,SVD也可以用于逆矩阵变换。拿三维空间举例:
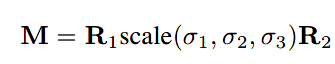
其逆矩阵为:
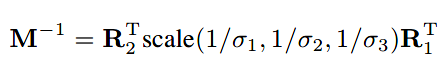
6.5坐标系变换(Coordinate Transformations)
上文所讲述的均是使用矩阵变换点的位置,我们也可以通过坐标系的变换来改变点的位置。如下图:
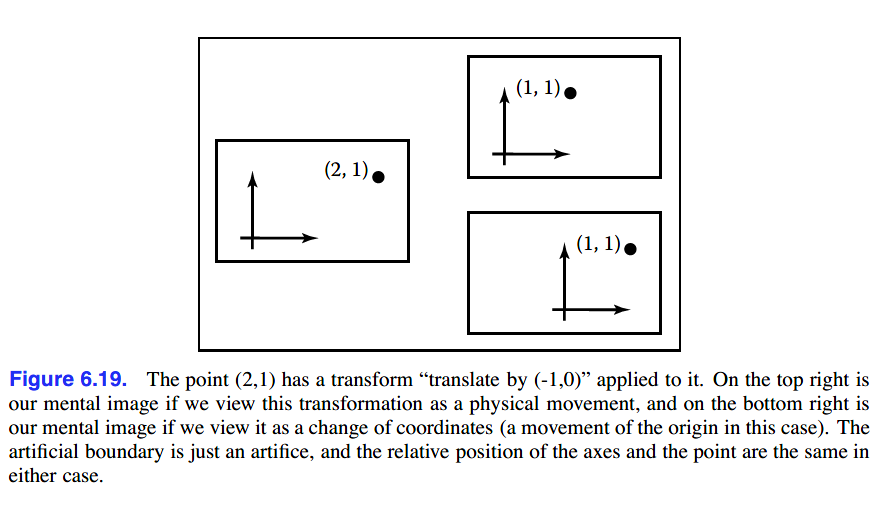
右上角是改变点的位置,右小角是该改变坐标系的位置。两种方式都改变了点在坐标系之中的位置。
当在操控一个具有多坐标系的场景中,为了避免混淆,会有一个全局坐标系(也称为世界坐标系)。比如下图,基于o、x、y的坐标系为全局坐标系,其他坐标系的原点、正交向量位置需要基于全局坐标系。
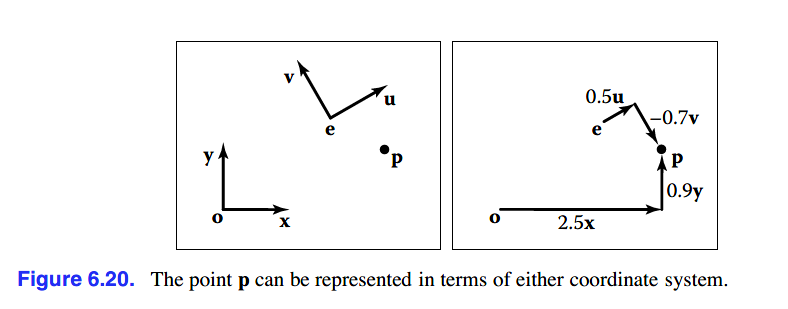
如上图,在各自的坐标系中可以如此表示其位置:
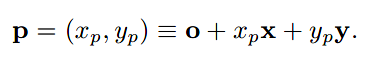
(xp, yp) = (2.5, 0.9)
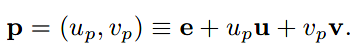
(up, vp) = (0.5, -0.7)
我们可以通过全局坐标系及e坐标系的位置关系把它们联系起来:
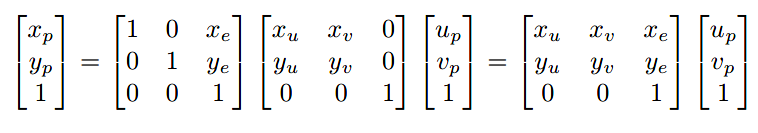
化简后如下:
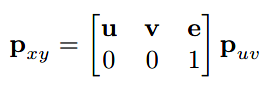
我们称此矩阵为(u, v)系统的*frame-to-canonical matrix *。将(u, v)体系中的值转化为全局坐标系中点相同位置的值。
当然,也有canonical-to-frame matrix:

三维场景中同理:

总结
通过此章学习,对于线性代数在计算机图形中的变换本质有了更深刻的理解,也了解到了线性代数的实用之处,在更加复杂的动画、变换之上可能更加需要。
以上内容若有不足之处,还请大佬指教。
参考资料
错切 - Wikipedia
反射 - Wikipedia
矩阵分解(Matrix decomposition) - Wikipedia
对称矩阵(symmetric matrix) - Wikipedia
转置矩阵 - Wikipedia
正交矩阵(orthogonal matrix) - Wikipedia
对角矩阵(diagonal matrix)- Wikipedia
单位矩阵(Identity matrix)
奇异矩阵(singular matrix)- 百度百科
逆矩阵(inverse matrix)- Wikipedia
线性方程组 - Wikipedia
特征值和特征向量 - Wikipedia
Linear Algebra 21i: How to Represent a Rotation with respect to an Arbitrary Axis - Youtube
仿射变换(Affine Transformations)- Wikipedia
什么是齐次坐标系?为什么要用齐次坐标系? - 格东西的回答 - 知乎
如何通俗地讲解「仿射变换」这个概念? - 马同学的回答 - 知乎
为什么引入齐次坐标的变换矩阵可以表示平移呢? - Yu Mao的回答 - 知乎