Java 图的最短路径dijstra(迪杰斯特拉)算法和拓扑排序

磊_lei
2,307 阅读4分钟
原文链接： lilei644.github.io

一、图的最短路径

从某顶点出发，沿图的边到达另一顶点所经过的路径中，各边上权值之和最小的一条路径叫做最短路径

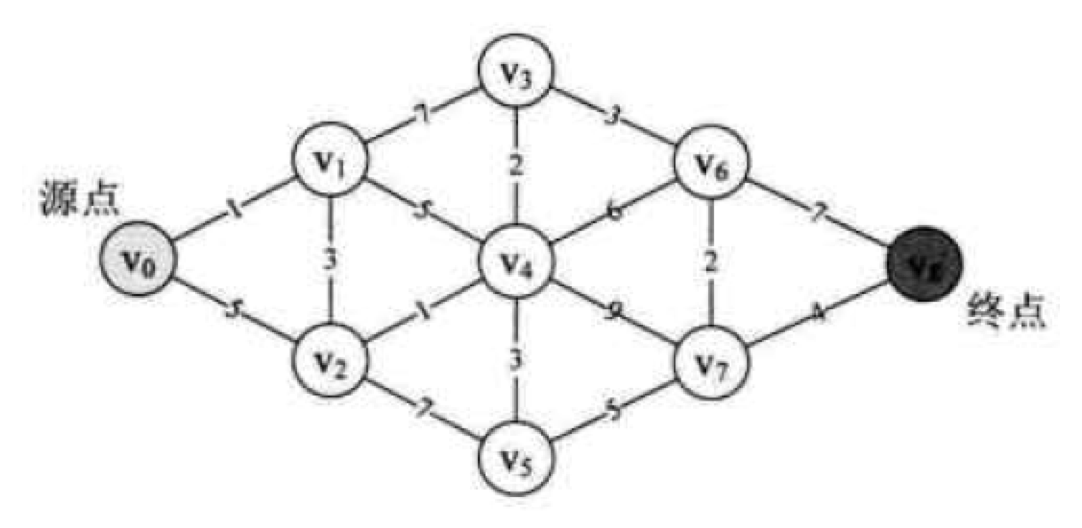
图的最短路径

图的最短路径有许多重要的应用。

例如：上图中v0-v8有9个点，可以看做不同的地点，现在要规划出v0到其它某个点地点的最短路线规划

构建最短路径中比较常见的一种算法即为dijstra(迪杰斯特拉)算法

二、dijstra(迪杰斯特拉)算法

算法思路：

  1. dijstra算法思路有点类似前一篇文章中的prim算法，先构建图的邻接矩阵，然后定义一个临时的一维数组，一维数组用来存储v0到每个顶点的最短路径
  2. 将一维数组初始化成v0到每个顶点的值。其次定义另外一个数组用来存储已经访问过的顶点
  3. 在临时一维数组中找到未被访问且最短的一条路径
  4. 将找到最短路径的顶点与该顶点可访问边进行遍历，若最短路径与边之和小于一维数组中存储的最短路径，则将这个和覆盖成这个顶点的最短路径
  5. 循环3，4直至遍历完所有顶点为止
  • 构建邻接矩阵
// 初始化图
int[] graph0 = new int[]{0, 1, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT};
int[] graph1 = new int[]{1, 0, 3, 7, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT};
int[] graph2 = new int[]{5, 3, 0, MAX_WEIGHT, 1, 7, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT};
int[] graph3 = new int[]{MAX_WEIGHT, 7, MAX_WEIGHT, 0, 2, MAX_WEIGHT, 3, MAX_WEIGHT, MAX_WEIGHT};
int[] graph4 = new int[]{MAX_WEIGHT, 5, 1, 2, 0, 3, 6, 9, MAX_WEIGHT};
int[] graph5 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 7, MAX_WEIGHT, 3, 0, MAX_WEIGHT, 5, MAX_WEIGHT};
int[] graph6 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 3, 6, MAX_WEIGHT, 0, 2, 7};
int[] graph7 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 9, 5, 2, 0, 4};
int[] graph8 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 5, 4, 0};
  • 算法代码
/**
 * 图的最短路径(图中两个顶点的最短距离)，迪杰斯特拉算法
 * 算法思想：类似prim算法，定义一个一维数组，用来存储V0到某点的最短路径
 */
public void shortestPathDijstra() {

    // 定义一维数组用来存储V0到每个点的最短路径，找到比原来更短的则直接覆盖
    int[] paths = new int[vertexSize];

    // 先将数组初始化
    System.arraycopy(matrix[0], 0, paths, 0, vertexSize);

    isVisited[0] = true;
    for (int i = 1; i < vertexSize; i++) {

        // 在已经存在的路径中找到一条未被访问且最短的路径
        int min = MAX_WEIGHT;
        int minIndex = -1;
        for (int j = 1; j < vertexSize; j++) {
            if (!isVisited[j] && paths[j] < min) {
                min = paths[j];
                minIndex = j;
            }
        }

        if (minIndex == -1) {
            continue;
        }
        isVisited[minIndex] = true;

        // 找到的最短路径节点的可使用边中，判断是否比已经存在的最短路径短，是则进行覆盖
        for (int k = 1; k < vertexSize; k++) {
            if (!isVisited[k] && (min + matrix[minIndex][k] < paths[k])) {
                paths[k] = min + matrix[minIndex][k];
            }
        }
    }

    for (int i = 1; i < vertexSize; i++) {
        System.out.println("V0到V" + i + "的最短路径为：" + paths[i]);
    }
}
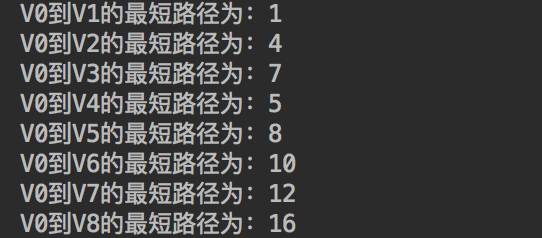
  • 即可得到v0到每个点的最短路径的值

dijstra最短路径

三、拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。

简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

对以下有向图进行拓扑排序，顶点可以看待成每项不同的任务，有的任务可以直接执行，例如v0、v1、v3，有的任务得等到上级任务全部执行完成才可执行，例如v4必须等到v0和v1都完成之后才可执行

拓扑排序

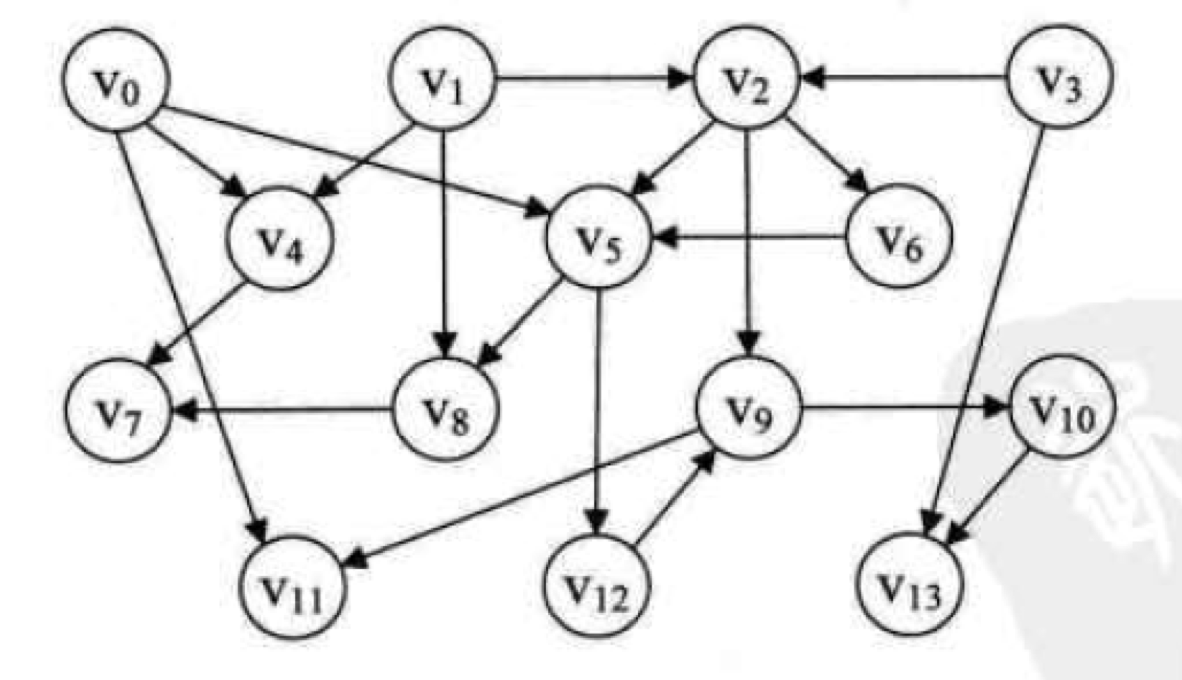
排序思路：

  1. 观察可以发现顶点入度为0则代表可以直接执行
  2. 完成一个任务之后可消除出度的边，即他的next节点则少了一个入度
  3. 带next节点入度也为0之后就可执行
  4. 循环1，2，3遍历完所有的顶点即可排序完成

排序代码：

  • 构建每个顶点的邻接表

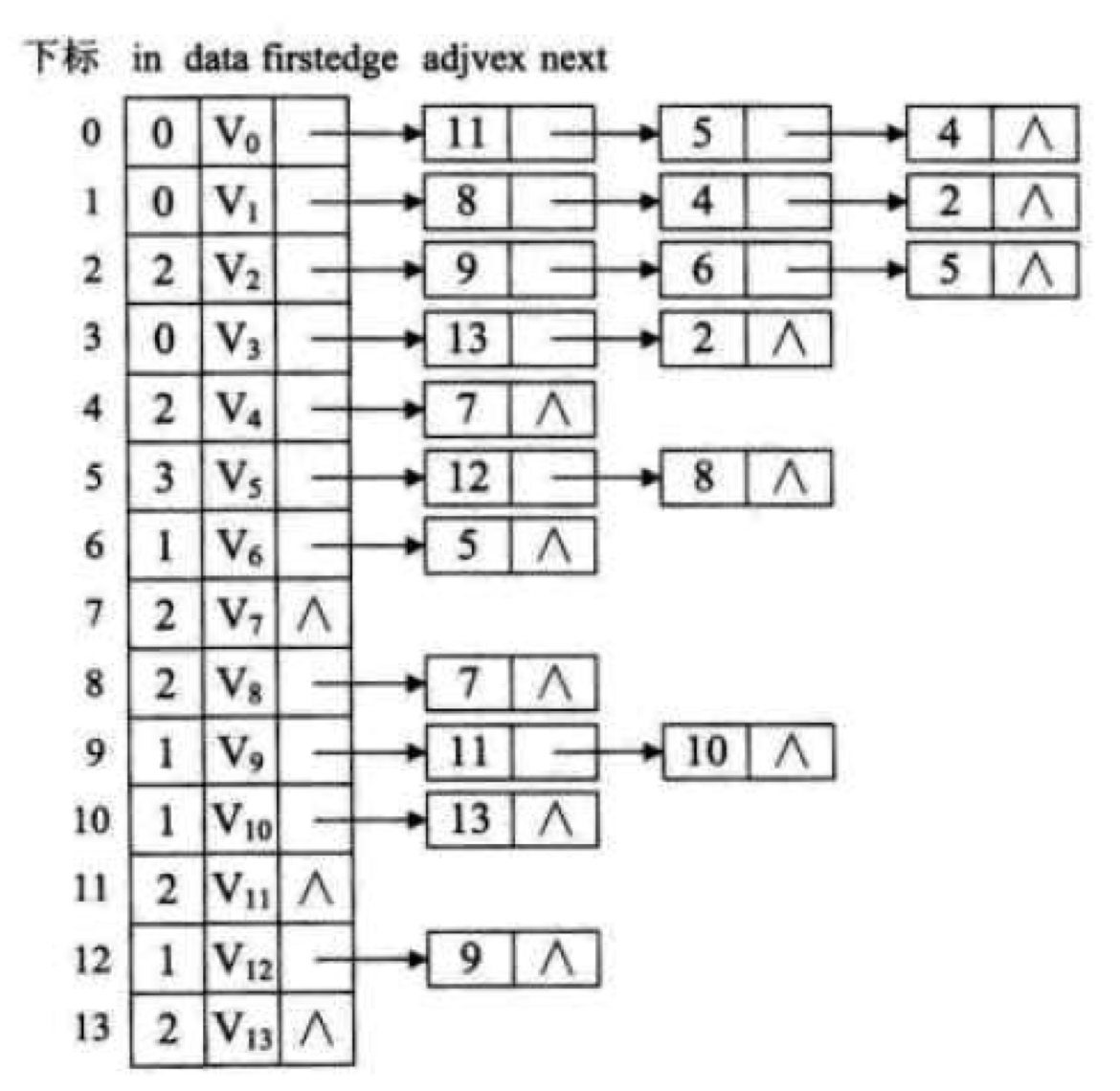
拓扑排序邻接点

  • 算法代码
/**
 * 拓扑排序
 * 思路：定义一个栈，存放入度为0的节点，入度为0则代表可以执行，执行之后则出度的那个节点就减少一个入度，循环直至栈为空
 */
private void topologicaSort() {
    Stack<Integer> stack = new Stack<>();

    // 先将入度为0 的节点压入栈中
    for (int i = 0; i < adjList.length; i++) {
        if (adjList[i].in == 0) {
            stack.push(i);
        }
    }

    int count = 0;
    // 循环出栈输出，直至栈为空
    while (!stack.isEmpty()) {
        int index = stack.pop();
        System.out.println("顶点：" + adjList[index].data);
        count++;
        for (EdgeNode edgeNode = adjList[index].firstEdge; edgeNode != null; edgeNode = edgeNode.next) {
            if (--adjList[edgeNode.adjVert].in == 0) {
                // 若输出之后的顶点入度也没0，则压入栈中
                stack.push(edgeNode.adjVert);
            }
        }
    }

    if (count != numVertexes) {
        System.out.println("拓扑排序失败！！！！");
    }
}
源码地址
avatar
文章
阅读
粉丝