Normalization

初始化 vs. 优化器优化

假如我们初始化选择 $W_i \sim N(0, \frac{c}{n})$ ，使用Relu作为激活函数且 $c \neq 2$

经过一些次数的优化迭代后，初始权重的尺度达到一个稳定值吗？

答案是否定的，对一个深度神经网络，如果初始化的时候选择了一个不好的权重，网络可能根本训练不起来(至少使用SGD方法时是这样的) 从上图右侧我们可以看到，当 $\sigma ^2 = \frac{2}{n}$ 时能够正常训练，其它两个选择要么会使得数值溢出，要么是训练不动。

然而更根本的是，即使不同的初始化权重训练成功了，初始化权重的影响在整个训练过程中都存在：

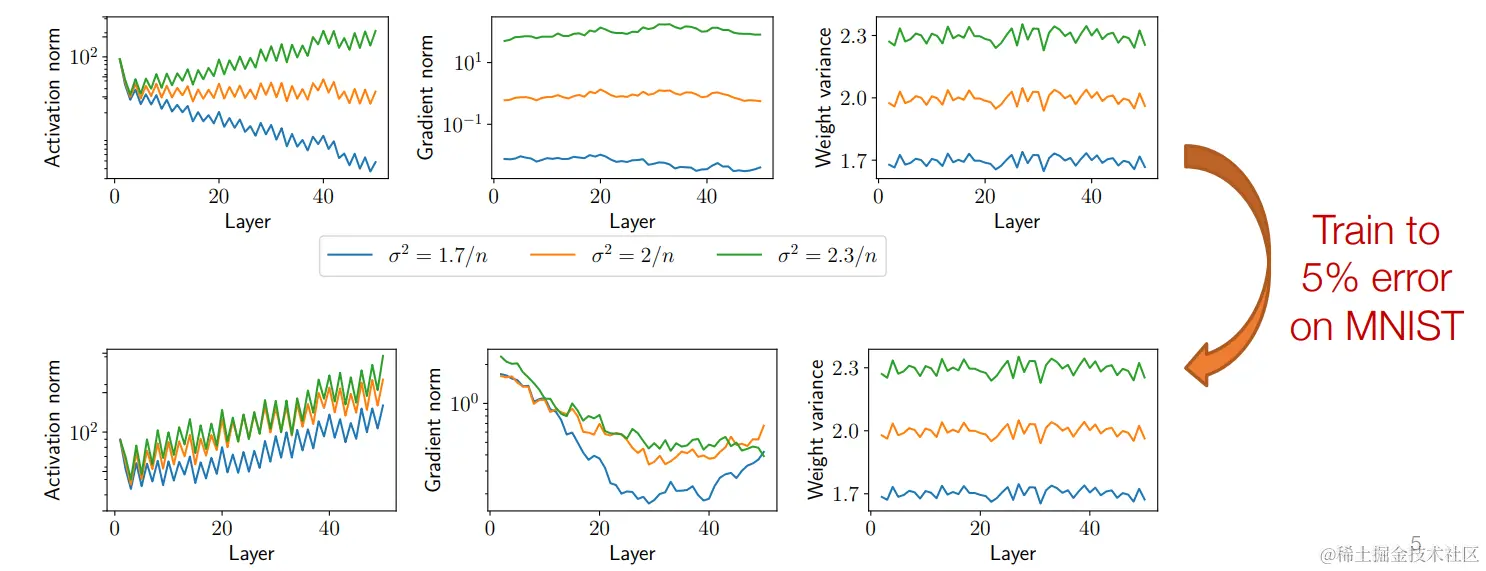
上图是用三个不同的 $\sigma^2$ 来初始化权重，上面三幅图是训练前每一层输出的范数、梯度的范数和权重的方差，下面三幅图则是训练完成后的同样参数。

可以从图像中看出，初始化的时，范数比其它初始化的范数大的，在训练完成后，范数还是偏大，而范数偏小的，训练完成同样偏小。但是权重的方差训练前后变化并不大，也说明了其实优化参数对参数的改动很小，这更说明了参数初始化的重要性。

初始化对训练非常重要，在训练过程中权重参数会发生变化，使各层/网络之间的输出范数不再 “一致”。

但是深度网络中的层可以是任何的一种计算，我们可以加入一种层，能够修正网络激活函数的输出到我们想要的尺度，这也叫做layer normalization。

Layer normalization

很自然的想法，我们对每一层的激活进行归一化（均值为零，方差为一），这就是所谓的层归一化（Layer normalization）

\begin{array}{l} \hat{z}_{i+1} = \sigma _i (W_i^T z_i +b_i) \\ z_{i+1} = \frac{\hat z_{i+1} - E[\hat z_{i+1}]}{(Var[\hat z_{i+1}] + \epsilon)^{1/2}} \end{array}

为每个项添加额外的标量权重和偏置也很常见（仅会改变表示方法，例如，如果我们将归一化放在非线性之前）。如：

\begin{array}{l} \hat{z}_{i+1} = \sigma _i (W_i^T z_i +b_i) \\ z'_{i+1} = \frac{\hat z_{i+1} - E[\hat z_{i+1}]}{(Var[\hat z_{i+1}] + \epsilon)^{1/2}}\\ z_{i+1} = W^T z'_{i+1} + b \end{array}

可以看到加了LayerNorm解决了激活函数后范数不统一的问题。

Batch normalization

一个奇怪的想法：我们考虑更新的矩阵形式

\hat{Z}_{i+1} = \sigma _i (Z_iW_i + b_i^T)

层归一化相当于把矩阵的行进行归一化。

如果我们考虑对矩阵的列进行归一化呢？对列进行归一化也叫做batch normalization，我们可以对小批量的激活数据进行归一化处理：

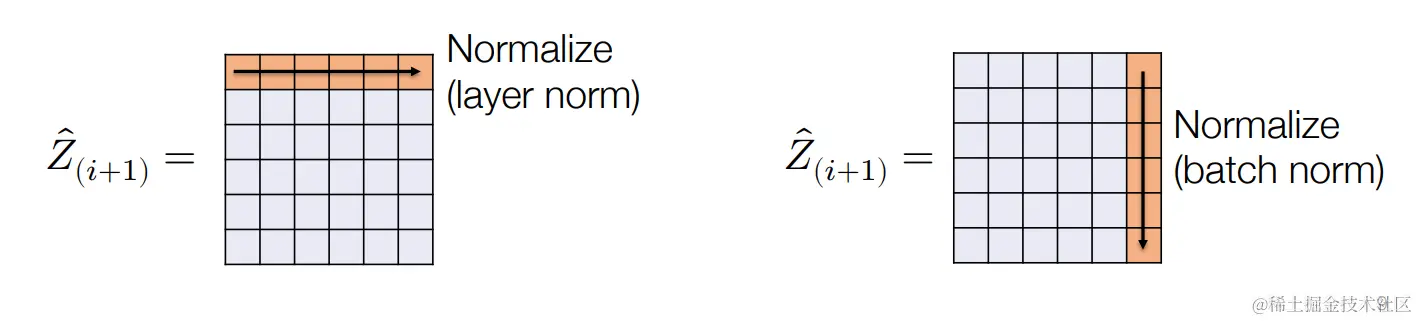
小批量存在依赖性

BatchNorm 的一个奇怪的点在于，它使每个示例的预测都取决于整批数据的分布，如果我们每层都计算所有数据的均值和方差，显然是不现实的。

常见的解决方案是计算每层的 $\hat \mu_{i+1}$ ， $\hat \sigma_{i+1}^2$ （平均值/方差）的运行平均值，并在测试时用这些量进行归一化处理。

(z_{i+1})_j = \frac{(\hat z_{i+1})_j -(\hat \mu _{i+1})_j}{((\hat \sigma ^2 _{i+1})_j + \epsilon)^{1/2}}

Regularization

通常深度神经网络（即使是很简单的两层神经网络）都是参数量过量的模型，有着比训练数据量要大很多的训练参数量。

这样网络模型可以很好的拟合这些训练数据

从传统的机器学习和统计学角度来说，这样的模型可能存在过拟合，泛化性没这么强的的问题。

但是这种网络模型的确在测试集上也有较好的泛化性
也不总是会出现过拟合的现象

正则化过程是“限制模型参数的复杂度”以确保网络模型对新数据有较好的泛化能力，在深度学习中通常有两种方法实现：

隐式正则化：指我们现有的算法（即 SGD）或架构已经限制了所考虑的函数的方式。

如，实际上，我们并不是对 "所有神经网络 "进行优化，而是在给定权重初始化的情况下，对 SGD 考虑的所有神经网络进行优化

显式正则化：是指对网络和训练程序所做的修改，其明确目的是使网络正则化。

$\ell_2$ 正则化（权重衰减）

从经典角度看，模型参数的大小往往是复杂性的合理代表，因此我们可以在保持参数较小的同时，尽量减少损失。我们可以将网络参数的 $\ell _2$ 范数加在我们需要优化的函数后面：

\underset{W_{1:L}}{minimize} \frac{1}{m} \sum_{i=1}^m \ell (h_{W_{1:L}}(x^{(i)}), y^{(i)}) + \frac{\lambda}{2} \sum_{i=1}^{L} \parallel W_i \parallel_2 ^2

由梯度下降方法更新参数的式子就更新如下：

W_i := W_i - \alpha \nabla_{W_i} \ell (h(X),y) - \alpha \lambda W_i = (1 - \alpha \lambda)W_i - \alpha \nabla_{W_i} \ell (h(X), y)

这样在训练过程中的每一轮迭代我们都减去了权重参数乘了 $(1 - \alpha \lambda)$ 这个放缩因子的大小

$\ell _2$ 正则的注意事项

$\ell _2$ 正则化是一种极为常见的深度学习方法，通常只是作为 "权重衰减 "项纳入优化程序中。

回顾我们采用不同的初始化参数训练的的神经网络：

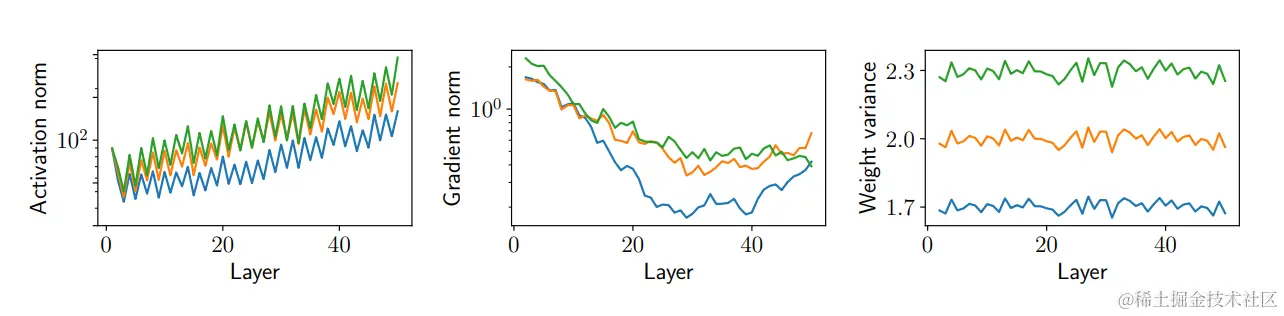
...参数大小可能无法代表深度网络的复杂性

Dropout

另一种常见的正则化策略：随机将每一层的部分激活值设为零:

\begin{array}l \hat z_{i+1} = \sigma _i (W_I^T z_i + b_i) \\ (z_{i+1})_j = \begin{cases} (\hat z_{i+1})_j / (1 - p) & with \ probability \ 1-p \\ 0 & with \ probability \ p \end{cases} \end{array}

(与 BatchNorm 不同）乍一看似乎很奇怪：这难道不会极大地改变被逼近的函数吗？

Dropout看作近似值

Dropout经常被使用在深度学习网络中，通过随机将激活函数值置0可以提高网络的健壮性（但是在测试的时候不使用Dropout，只在训练的时候使用）

\begin{aligned} \frac{1}{m} \sum_{i=1}^{m} \ell\left(h\left(x^{(i)}\right), y^{(i)}\right) & \Longrightarrow \frac{1}{|B|} \sum_{i \in B} \ell\left(h\left(x^{(i)}\right), y^{(i)}\right) \\ z_{i+1}=\sigma_{i}\left(\sum_{j=1}^{n} W_{j,:}\left(z_{i}\right)_{j}\right) & \Longrightarrow z_{i+1}=\sigma_{i}\left(\frac{n}{|\mathcal{P}|} \sum_{j \in \mathcal{P}}^{n} W_{j,:}\left(z_{i}\right)_{j}\right) \end{aligned}

优化、初始化、规范化、正则化的相互作用

许多设计选择旨在简化深度网络的优化能力

Choice of optimizer learning rate / momentum
Choice of weight initialization
Normalization layer
Reguarlization

这些还不包括我们在以后的讲座中会涉及到的许多其他 "技巧"：残差连接、学习率时间表，以及其他的内容。

...如果你觉得深度学习的实践就是用大量 GPU 胡乱炼丹，那就大错特错了。

总结

不要有一种刻板印象，认为深度学习都是一些随意的黑客行为：在上述所有方面，已经有了很多出色的科学实验。

但我们确实无法完全了解人们使用的各种经验技巧究竟是如何工作和相互作用的。

"好消息 "是，在很多情况下，似乎可以通过完全不同的架构和方法选择获得类似的好结果。

Deep Learning Systems: Normalization and Regularization规范化和正则化