图形学初识--视图+投影变换

航火火
2,221 阅读6分钟

前言

前面章节主要讲解了一些常用的变换矩阵，这一节咱们主要讲解一些视图变换和投影变换。

有些小伙伴可能不了解图形学，会有所疑惑这些矩阵有啥用，其实这都是为了后面"MVP变换"做铺垫，但是如果一上来冒然的介绍MVP，会因小失大！因此作者决定将其放在后面介绍渲染管线的时候介绍它，不要着急哦！

正文

视图变换

为什么要有视图变换？

想象一个三维场景中，各个地方的物体已经摆好了。这时候有一个好奇心宝宝，想要从不同的视角去观察，物体摆放的合不合适，那怎么办呢？

答：需要引入类似"摄像机"的概念，就像现实中一样，摄像师扛着摄像机跑，从而拍到了不同的画面，虚拟的三维场景也是一样！为此引入视图变换，来满足虚拟摄像机的需求！

视图变换是什么？

本质上，它和前面章节提到的旋转变换、平移变换类似，最终结果呈现也就是一个矩阵的表达式罢了。

视图变换如何定义？

定义摄像机：

让我们思考一个问题，如果我们是摄影师，需要某漂亮国的一处景点，摄像机需要有哪些属性呢？

答：摄像机的位置、摄像机镜头朝向、摄像机顶部朝向等等。

人都是懒的，如果在三维空间中为了方便显示在二维中，最简单的摄像机如下所示：

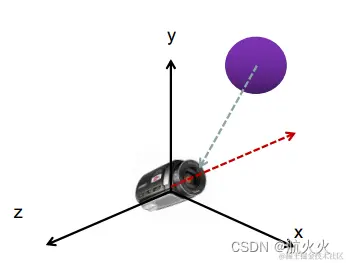
在这里插入图片描述

摄像机相关属性：

  • 位置摆放在原点
  • 摄像机镜头朝向-z轴方向

此时这种情况，所有物体都可以直接沿着z轴投射到摄像机的屏幕中，非常方便！

但是往往事与愿违，如果摄像机变化到下述的形态，就不方便直接按照z轴投射了！

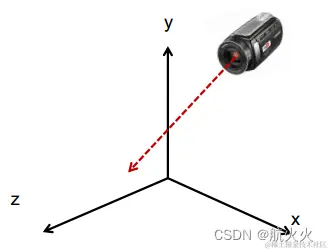
在这里插入图片描述

所以，我们就需要达成一个目标：将摄像机恢复到原点，并且镜头朝向-z轴！

摄像机变换：

这个问题如何思考呢？其实我们可以逆过程思考，我们可以想一想：原本在原点并看向-z轴的一台摄像机，是如何变化到上述情况的！

然后咱们上述目标的达成也就是应用此过程的逆变换！

正向过程变换示意图如下：

1、摄像机先绕原点旋转

2、摄像机进行平移

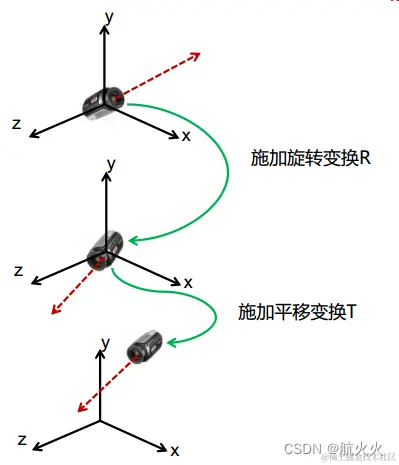
在这里插入图片描述

自之前章节的学习，我们知道，这个过程也就可以表述为：先旋转变换，再平移变换。公式如下：

M=T∗R注：R为旋转矩阵，T为平移矩阵M = T * R\\ 注：R为旋转矩阵，T为平移矩阵

上述的逆变换也就显而易见：

M−1=R−1∗T−1M^{-1} = R^{-1}*T^{-1}

所以，只要应用此变换，就可以实现将任意位置和朝向的摄像机，变换到位于原点并看向-z轴的情形！如下示意图：

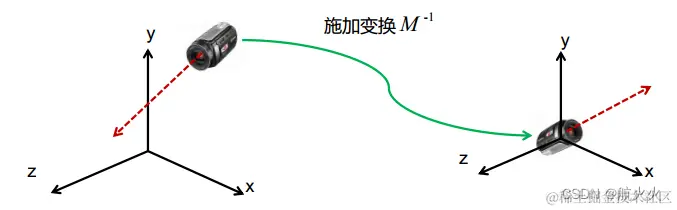
在这里插入图片描述

目标重申：

既然我们要求场景的物体和摄像机保持相对静止，那么只需要针对所有物体进行上述的变换，不就实现了咱们的目标么！Successfully！

构建矩阵：

为了方便，咱们定义摄像机朝向为：front⃗\vec {front} 向量，简称f⃗\vec f ；摄像机顶部向量为 u⃗\vec u ，以及一个摄像机的 right⃗\vec {right} 向量，简称: r⃗\vec r ，示意图如下：

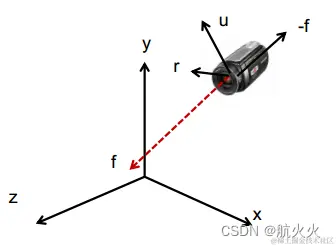
在这里插入图片描述

既然咱们已经知道了新的坐标系的三个基向量r⃗、u⃗、−f⃗\vec{r}、\vec{u}、\vec{-f} ，分别对应于心坐标系的x、y、z轴，所以咱们自然而然就知道了旋转矩阵 RR，如下：

R=[rxux−fx0ryuy−fy0rzuz−fz00001]R = \begin{bmatrix} r_x & u_x & -f_x & 0\\ r_y & u_y & -f_y & 0\\ r_z & u_z & -f_z & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

所以咱们可以自然而然得到R的逆矩阵，如下：

R−1=[rxryrz0uxuyuz0−fx−fy−fz00001]R^{-1}=\begin{bmatrix} r_x & r_y & r_z & 0\\ u_x & u_y & u_z & 0\\ -f_x & -f_y & -f_z & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

我们假设摄像机的位置位于：P=(px,py,pz)P = (p_x,p_y,p_z) ，则可以构建一下的平移矩阵及其逆矩阵：

T=[100px010py001pz0001]T=\begin{bmatrix} 1 & 0 & 0 & p_x\\ 0 & 1 & 0 & p_y\\ 0 & 0 & 1 & p_z\\ 0 & 0 & 0 & 1\\ \end{bmatrix}\\
T−1=[100−px010−py001−pz0001]T^{-1}=\begin{bmatrix} 1 & 0 & 0 & -p_x\\ 0 & 1 & 0 & -p_y\\ 0 & 0 & 1 & -p_z\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

根据之前的结论，视图变换矩阵为：M−1=R−1∗T−1M^{-1} = R^{-1}*T^{-1}，因此如下：

M−1=[rxryrz0uxuyuz0−fx−fy−fz00001]∗[100−px010−py001−pz0001]=[rxryrz−r⃗⋅p⃗uxuyuz−u⃗⋅p⃗−fx−fy−fzf⃗⋅p⃗0001]\begin{align} M^{-1}&=\begin{bmatrix} r_x & r_y & r_z & 0\\ u_x & u_y & u_z & 0\\ -f_x & -f_y & -f_z & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}*\begin{bmatrix} 1 & 0 & 0 & -p_x\\ 0 & 1 & 0 & -p_y\\ 0 & 0 & 1 & -p_z\\ 0 & 0 & 0 & 1\\ \end{bmatrix}\\ &= \begin{bmatrix} r_x & r_y & r_z & -\vec{r} \cdot \vec{p}\\ u_x & u_y & u_z & -\vec{u} \cdot \vec{p}\\ -f_x & -f_y & -f_z & \vec{f} \cdot \vec{p}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{align}

总结： 为了灵活的从摄像机视角观察物体，并且方便按照z轴投射，咱们只需要针对三维场景的物体应用上述的变换矩阵即可！

投影变换

1、正交投影

正交投影是什么？

它是一种平行投影，用于将三维空间场景映射到2D的平面上。直观上理解，有点类似截面图或者压扁了的感觉！所以它本质上没有所谓的近大远小的特点。如图所示

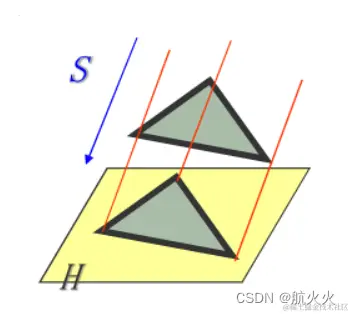
在这里插入图片描述

它常常应用于CAD制图等领域！

为什么需要正交投影？

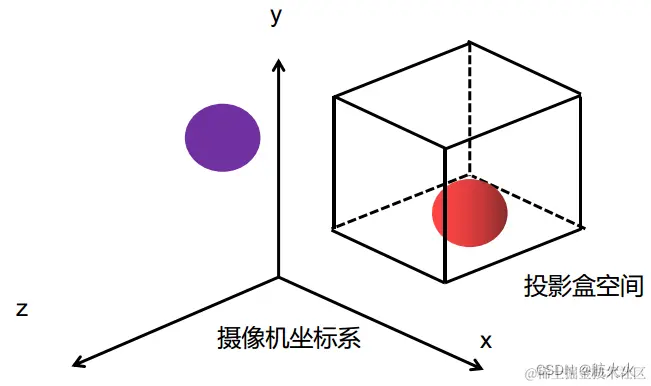
1、实际上，在三维场景中，我们的物体范围可能非常大，但是咱们屏幕空间是有限的，所以为了关注特别需要的区域，需要定义一个类似包围盒体的东西，盒体的需要显示，盒体外的咱们不需要显示

2、为了规范化坐标为NDC坐标，方便后续在屏幕中显示

NDC坐标，其实就是一个x、y、z都在 [-1,1] 范围内的规范化的坐标！

如图所示：

在这里插入图片描述

正交投影矩阵是啥？

（1）约定以下都在视图变换后的摄像机坐标系下定义。

一个立方体包围盒，也就是上、下、左、右、前、后这几个属性定义而成，如图所示：

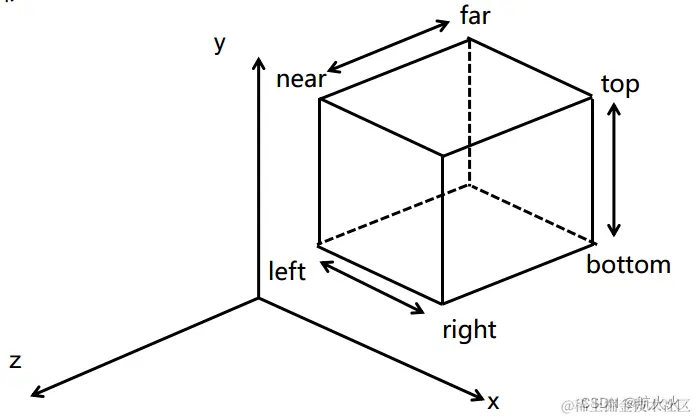
在这里插入图片描述

（2）为了达到NDC坐标的 [−1,1]3[-1,1]^3 的要求，我们需要规范两件事情：

  • 盒体中心规范到原点
  • 盒体长度缩放至2X2X2的标准长度

因此，上述操作也就对应两个变换矩阵，先平移到中心，再进行缩放。

我们定义包围盒体的x范围：[l,r][l,r]，y范围：[b,t][b,t]，z范围：[n,f][n,f]，因而我们得出以下平移矩阵和缩放矩阵：

T=[100−r+l2100−t+b2100−n+f20001]T= \begin{bmatrix} 1&0&0&-\frac{r+l}{2}\\ 1&0&0&-\frac{t+b}{2}\\ 1&0&0&-\frac{n+f}{2}\\ 0&0&0&1\\ \end{bmatrix}
S=[2r−l00002t−b00002f−n00001]S= \begin{bmatrix} \frac{2}{r-l}&0&0&0\\ 0&\frac{2}{t-b}&0&0\\ 0&0&\frac{2}{f-n}&0\\ 0&0&0&1\\ \end{bmatrix}

从而我们得到正交投影变换矩阵：Ortho=S∗TOrtho = S*T

Ortho=[2r−l00−r+lr−l02t−b0−t+bt−b002f−n−n+ff−n0001]Ortho= \begin{bmatrix} \frac{2}{r-l}&0&0&-\frac{r+l}{r-l}\\ 0&\frac{2}{t-b}&0&-\frac{t+b}{t-b}\\ 0&0&\frac{2}{f-n}&-\frac{n+f}{f-n}\\ 0&0&0&1\\ \end{bmatrix}

2、透视投影

为什么需要透视投影？

上面的正交投影已经说过，它最大的缺点就是没有近大远小的特性，但是在现实中如果没有这样的特性，几乎三维场景就是非常"假"的一个状态。

因此，为了能够体现近大远小的特性，又发明了透视投影这一说。有点类似于素描的“透视”的概念！

透视投影是什么？

视线从摄像机触发，看向-z轴方向，可视范围为near到far的一个视锥体。最终所有物体都达到近平面near上！如下图所示：

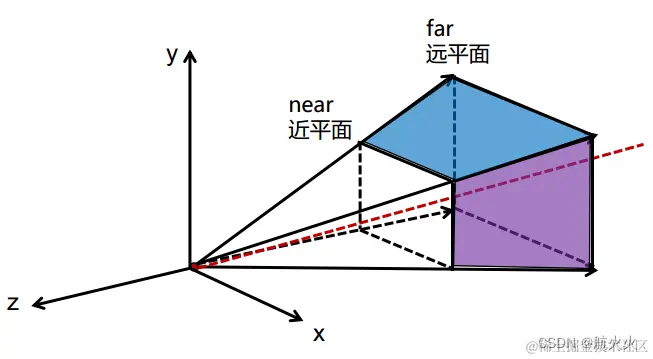
在这里插入图片描述

如何定义透视投影变换？

既然知道最终所有物体都投射到近平面上，因此我们将增加几个近平面的属性，完善一下上述的示意图：

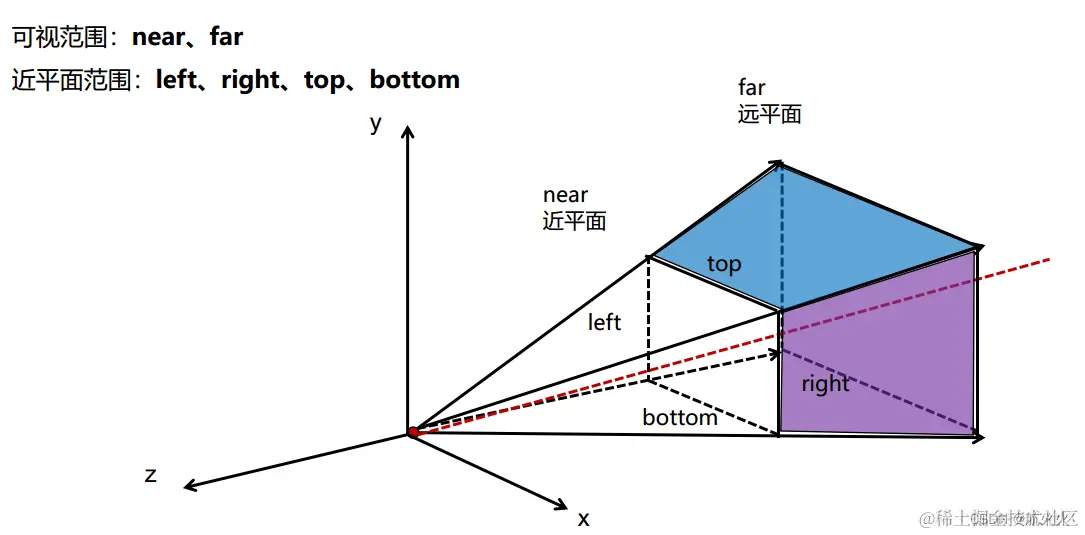
在这里插入图片描述

**重新定义以下透视投影变换最终目的：**将视锥体内的物体坐标变换至xyz都为[-1,1]的标准NDC坐标，如下图所示：

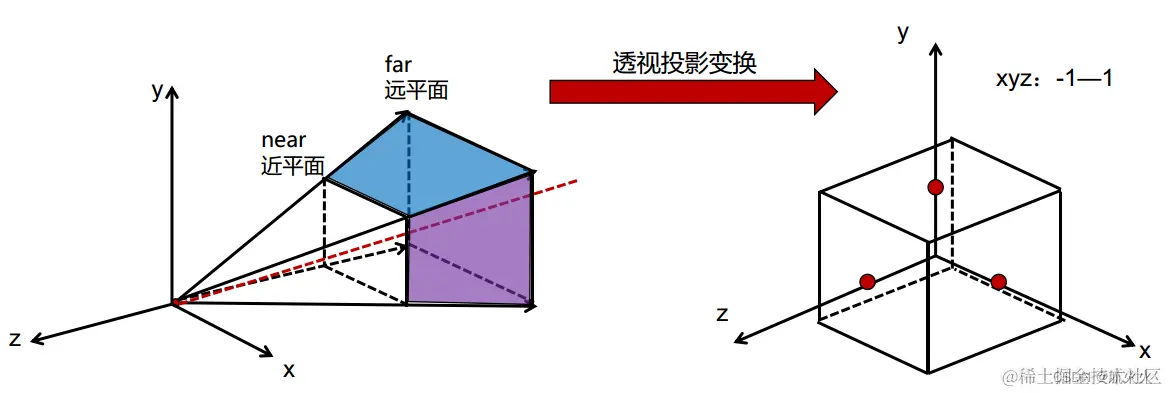
在这里插入图片描述

开始推导投影变换矩阵：

（1）基本思路：

  • 因为我们无法直接对矩阵得知，我们需要从投影前后的坐标关系进行反推矩阵
  • 又因为最终坐标是达到近平面上得，所以以此作为突破口

（2）咱们逆y轴进行俯视观察上述示意图，得到下面得截面图：

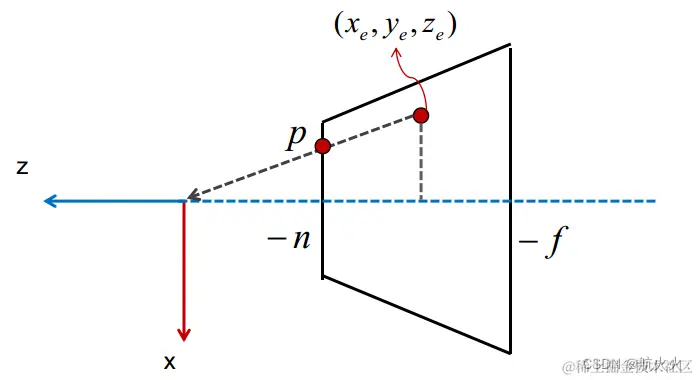
在这里插入图片描述

假设某一个摄像机坐标系下得坐标为 (xe,ye,ze)(x_e,y_e,z_e) ，它投影到进平面后，得到 p=(xp,yp,zp)p=(x_p,y_p,z_p) ，根据相似三角形可以得到如下等式：

xpxe=−nze\frac{x_p}{x_e} = \frac{-n}{z_e}

从而咱们得到投影到近平面上点的x坐标：xp=nxe−zex_p = \frac{nx_e}{-z_e}

（3）类似的，咱们逆x轴进行观察，得到下面得截面图：

在这里插入图片描述

也可以类似得到进平面上的y坐标：yp=nye−zey_p = \frac{ny_e}{-z_e}

有人可能发现了，这里的z_e不能为0，因为它在分母上，这个问题马上后面就会处理掉，大家不要着急！

（4）目前已得到投影到进平面上点的坐标，接下来要对其进行缩放到标准的[-1,1]的NDC坐标内

这里以y坐标为例，因为近平面是和z=0的平面平行关系，所以他们的缩放也必定是线性关系，如下示意图：

在这里插入图片描述

已知两点(t,1),(b,−1)(t,1),(b,-1)， 因此咱们可以计算出 yp和yndcy_p和y_{ndc} 关系如下：

yndc=2t−byp−t+bt−by_{ndc} = \frac{2}{t-b}y_p - \frac{t+b}{t-b}

同理可以得到 xp和xndcx_p和x_{ndc} 的关系，如下：

xndc=2r−lyp−r+lr−lx_{ndc} = \frac{2}{r-l}y_p - \frac{r+l}{r-l}

这里我们根据之前求的 yp和yey_p和y_e的关系、xp和xex_p和x_e的关系，进行等式替换，得到如下：

当ze≠0时xndc=2r−lyp−r+lr−l=2r−l∗nxe−ze−r+lr−l=1−ze(2nr−lxe+r+lr−lze)\begin{align} 当&z_e \neq 0时\\ x_{ndc} &= \frac{2}{r-l}y_p - \frac{r+l}{r-l}\\ &= \frac{2}{r-l}*\frac{nx_e}{-z_e} - \frac{r+l}{r-l}\\ &= \frac{1}{-z_e}(\frac{2n}{r-l}x_e + \frac{r+l}{r-l}z_e) \end{align}

同理，得到：

当ze≠0时yndc=2r−lyp−r+lr−l=2r−l∗nxe−ze−r+lr−l=1−ze(2nt−bye+t+bt−bye)\begin{align} 当&z_e \neq 0时\\ y_{ndc} &= \frac{2}{r-l}y_p - \frac{r+l}{r-l}\\ &= \frac{2}{r-l}*\frac{nx_e}{-z_e} - \frac{r+l}{r-l}\\ &= \frac{1}{-z_e}(\frac{2n}{t-b}y_e + \frac{t+b}{t-b}y_e) \end{align}

于是我们得到了xndc和yndcx_{ndc}和y_{ndc}的坐标表示，但是此时zndcz_{ndc} 还未知，并且上述也不能兼容ze==0z_e == 0的情况，所以咱们继续扩充知识

（5）利用齐次坐标，引入剪裁空间

既然上述由于除法的存在，导致分母为0的情况需要特殊考虑，人总是懒惰的，既然如此，有没有兼容=0的考虑方法呢？

答： 有的，那就将分母给去掉，只需要乘−ze-z_e即可

咱们因此剪裁空间的概念，由于剪裁的英文为clip，所以咱们定义如下：

pc(x)=xndc∗(−ze)=2nr−lxe+r+lr−lzepc(y)=yndc∗(−ze)=2nt−bye+t+bt−bzepc(z)= ?pc(w)=−ze\begin{align} p_c(x) &= x_{ndc}*(-z_e) = \frac{2n}{r-l}x_e + \frac{r+l}{r-l}z_e\\ p_c(y) &= y_{ndc}*(-z_e) = \frac{2n}{t-b}y_e + \frac{t+b}{t-b}z_e\\ p_c(z) &= \ ?\\ p_c(w) &= -z_e \end{align}

（6）已经考虑的差不多了，回归本源，开始利用坐标前后关系进行反推投影变换矩阵

这里先从 pc(w)=−zep_c(w) = -z_e 作为突破口，我们可以得到如下的关系：

(xcyczcwc)=(????????????00−10)(xeyezewe)\begin{pmatrix} x_c\\y_c\\z_c\\w_c \end{pmatrix} =\begin{pmatrix} ?&?&?&?\\ ?&?&?&?\\ ?&?&?&?\\ 0&0&-1&0\\ \end{pmatrix} \begin{pmatrix} x_e\\y_e\\z_e\\w_e \end{pmatrix}

然后再利用x、y坐标的前后关系，可以补齐前两行：

(xcyczcwc)=(2nr−l0r+lr−l002nt−bt+bt−b0????00−10)(xeyezewe)\begin{pmatrix} x_c\\y_c\\z_c\\w_c \end{pmatrix} =\begin{pmatrix} \frac{2n}{r-l}&0&\frac{r+l}{r-l}&0\\ 0&\frac{2n}{t-b}&\frac{t+b}{t-b}&0\\ ?&?&?&?\\ 0&0&-1&0\\ \end{pmatrix} \begin{pmatrix} x_e\\y_e\\z_e\\w_e \end{pmatrix}

（7）此时只剩跟z坐标相关的第三行的矩阵元素未知，需要回忆回忆额外的条件才行

我们知道，原本位于近平面上的坐标，无论x、y取什么值，它的坐标ze=−nz_e = -n 是一直成立的，也就是说与xy无关，所以咱们可以补充第三行的前两个参数，并且设后两个为A和B

(xcyczcwc)=(2nr−l0r+lr−l002nt−bt+bt−b000AB00−10)(xeyezewe)\begin{pmatrix} x_c\\y_c\\z_c\\w_c \end{pmatrix} =\begin{pmatrix} \frac{2n}{r-l}&0&\frac{r+l}{r-l}&0\\ 0&\frac{2n}{t-b}&\frac{t+b}{t-b}&0\\ 0&0&A&B\\ 0&0&-1&0\\ \end{pmatrix} \begin{pmatrix} x_e\\y_e\\z_e\\w_e \end{pmatrix}

既然我们知道任意的近平面上的点的z值，最终映射到ndc坐标空间都是-1；远平面上的点的z值，映射到ndc坐标上都是1，于是我们得到以下两个条件：

当ze=−n，we=1时=>zndc=−1=>zc=−ze∗zndc=−n当ze=−f，we=1时=>zndc=1=>zc=−ze∗zndc=f当z_e = -n，w_e = 1时 => z_{ndc}=-1 => z_c = -z_e * z_{ndc} = -n\\ 当z_e = -f，w_e = 1时 => z_{ndc}= 1 => z_c = -z_e * z_{ndc} = f

咱们可以用待定系数法， 代入得到以下等式：

A∗(−n)+B=−nA∗(−f)+B=fA*(-n) + B = -n\\ A*(-f) + B = f

然后咱们解个二元一次方程组，即可得到：

A=−f+nf−nB=−2fnf−nA = -\frac{f+n}{f-n}\\ B = \frac{-2fn}{f-n}

于是咱们得到最终的投影变换矩阵，如下：

Perspective=(2nr−l0r+lr−l002nt−bt+bt−b000−f+nf−n−2fnf−n00−10)Perspective = \begin{pmatrix} \frac{2n}{r-l}&0&\frac{r+l}{r-l}&0\\ 0&\frac{2n}{t-b}&\frac{t+b}{t-b}&0\\ 0&0&-\frac{f+n}{f-n}&\frac{-2fn}{f-n}\\ 0&0&-1&0\\ \end{pmatrix}

透视投影矩阵的工程化（参数变换）

上面我们已经知道了，构造透视投影矩阵需要以下已知参数：

  • 近平面n，原平面f
  • 近平面的b、t、l、r

但是，在实际工程中，这样的参数设置是比较麻烦的，所以咱们引入两个新的概念：

  1. y方向上的视张角fovy
  2. 近平面的纵横比aspect

额外补充条件：并且要求近平面相对y轴左右对称，相对x轴上下对称，如下图所示：

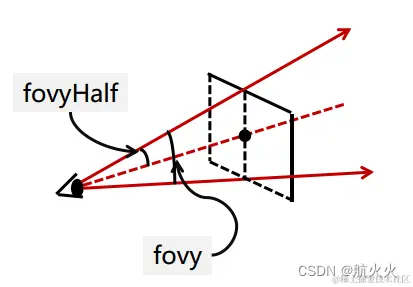
在这里插入图片描述

咱们进行如下的参数替换：

  • 令t−b=2tan⁡(fovy/2)∗nt-b = 2\tan(fovy /2) * n

  • 令r−l=aspect∗(t−b)=2aspect∗tan⁡(fovy/2)∗nr-l = aspect*(t-b) = 2aspect*\tan(fovy / 2) * n​

因而可以推导出矩阵的所有元素替换，得到如下的最终结果：

Perspective=(1aspect∗tan(fovy/2)00001tan(fovy/2)0000−f+nf−n−2fnf−n00−10)Perspective = \begin{pmatrix} \frac{1}{aspect*tan(fovy/2)}&0&0&0\\ 0&\frac{1}{tan(fovy/2)}&0&0\\ 0&0&-\frac{f+n}{f-n}&\frac{-2fn}{f-n}\\ 0&0&-1&0\\ \end{pmatrix}

总结： 不管是透视投影还是正交投影，最终的目的都是讲摄像机坐标系下的坐标，最终变换到NDC坐标系下！

结尾：喜欢的小伙伴点点关注+赞哦!

你们的点赞就是我创作的最大动力！希望对各位小伙伴能够有所帮助哦，永远在学习的道路上伴你而行， 我是航火火，火一般的男人！

avatar
文章
阅读
粉丝