图形学初识--三角形重心坐标插值算法（小白狂喜）

航火火
32 阅读2分钟

前言

前面咱们发了两篇文章，主要讲了直线光栅化和直线插值的内容，这一节咱们聊一聊三角形插值算法，主要就是利用重心坐标公式。先忽略如何进行三角形光栅化的内容，后面有时间可以补上！

正文

为什么需要三角形插值？

关于直线插值在前面文章已描述过，针对三角形插值，思想也是类似。简要描述下：

如果我们知道屏幕上三角形的三个顶点各自的属性值，如何得知三角形内部覆盖所有像素位置的属性值呢？

这个问题的答案就是回答！

什么是三角形插值？

这里就用数学符号简易的描述下：

已知三角形的三个顶点 v0v_0、v1v_1、v2v_2，每个顶点的属性值 f(v0)f(v_0)、f(v1)f(v_1)、f(v2)f(v_2)，要求计算所有三角形内的顶点 vinv_{in}的属性值 f(vin)?f(v_{in})?

如何进行三角形插值？

虽然可能也会有别的三角形插值算法，但是咱们重点介绍：重心坐标插值算法！

1、结论

对于三角形 △ABC\triangle ABC 内任意一点 pp，都存在 0<α、β、γ<1且α+β+γ=10 < \alpha、\beta、\gamma < 1 且 \alpha + \beta + \gamma = 1 ，使得f(p)=αf(A)+βf(B)+γf(C)f(p) = \alpha f(A) + \beta f(B) + \gamma f(C)

为了更好的简述算法核心内容，咱们忽略三角形边界情况，也就不考虑取0和1的情况啦！

2、核心理解

通过观察上面的结论，给人的感觉就像是，只要通过三角形三个顶点属性值的加权混合，就可以获得三角形内部任何位置的顶点的属性值！

3、几何理解-重心坐标公式推导

（1）已知三角形△ABC\triangle ABC，其中一点PP 位于三角形内部

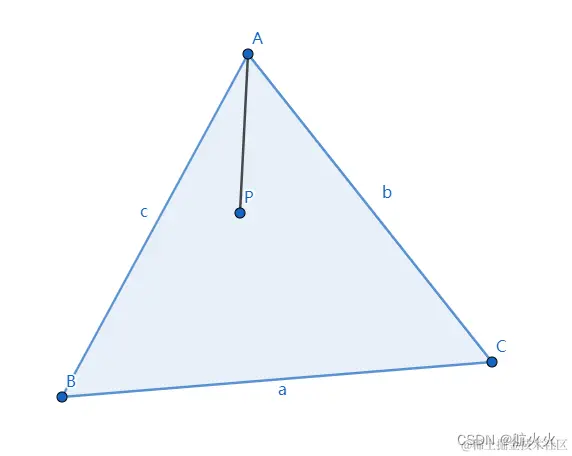
在这里插入图片描述

（2） 借助向量辅助推导，推导出顶点P和A、B、C的关系

∵向量AB⃗,AC⃗线性无关∴一定∃常数β、γ使得AP⃗=βAB⃗+γAC⃗∵AB⃗=B−A，AC⃗=C−A，AP⃗=P−A∴P−A=β(B−A)+γ(C−A)∴P=(1−β−γ)A+βB+γC记α=1−β−γ,从而∃(α+β+γ=1),使得P=αA+βB+γC\begin{aligned} &\because 向量 \vec{AB} , \vec{AC} 线性无关\\ &\therefore 一定 \exists 常数 \beta、\gamma 使得\vec{AP} = \beta\vec{AB} + \gamma\vec{AC}\\ &\because\vec{AB} = B-A，\vec{AC} = C-A，\vec{AP} = P-A\\ &\therefore P - A = \beta(B-A) + \gamma(C-A)\\ &\therefore P = (1 - \beta - \gamma)A + \beta B + \gamma C\\ &记\alpha = 1 - \beta - \gamma,从而\exists (\alpha + \beta + \gamma = 1),使得P = \alpha A + \beta B + \gamma C\\ \end{aligned}

（3）接下来的关键就是求解三个常数系数：α\alpha、 β\beta、 γ\gamma 的值

​ 针对上述的△ABC\triangle ABC ，咱们需要作点P和点B分别到直线AC的垂线，交点分别记作 DD 和 EE，然后连接PC

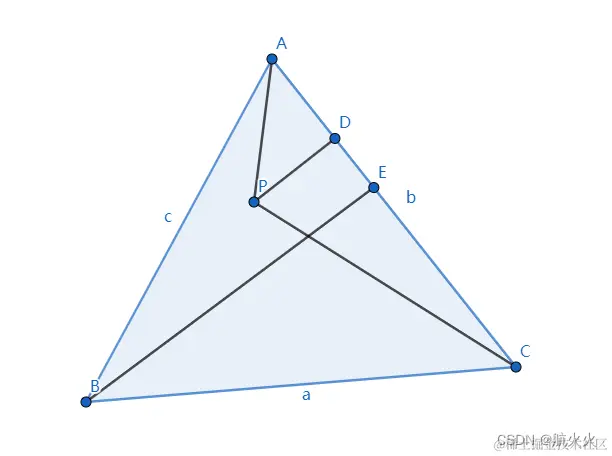
在这里插入图片描述

这里分别计算△ABC\triangle ABC和△APC\triangle APC的面积：

SAPC=0.5∗AC∗PDSABC=0.5∗AC∗BE上下两式相除，得到:SAPCSABC=PDBE记PD=hp，BE=hbS_{APC} = 0.5 * AC * PD\\ S_{ABC} = 0.5 * AC * BE\\ 上下两式相除，得到: \frac{S_{APC}}{S_{ABC}} = \frac{PD}{BE}\\ 记PD = h_p，BE = h_b

（4）上述的计算看似没啥用，但是我们可以联想相似三角形的知识，类比转换！

做辅助线：过P点做垂直于PD的直线 l1l_1，交线段AB于点F。然后过点F做平行线 l2l_2交线段AC于点G，如下图所示：

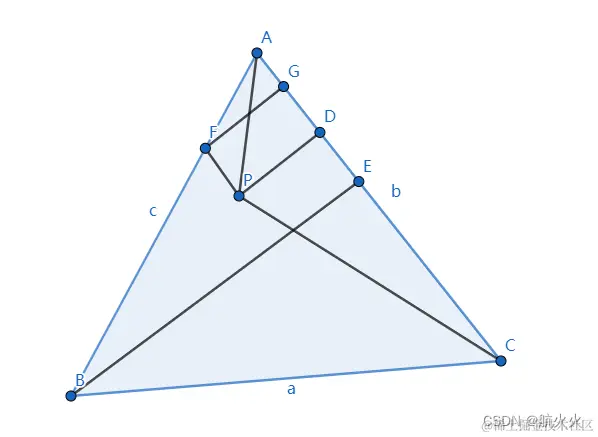
在这里插入图片描述

（5）向量加法几何理解突破

因为四边形PFGD是矩形，所以PD==FGPD == FG，结合之前的公式：SAPCSABC=PDBE\frac{S_{APC}}{S_{ABC}} = \frac{PD}{BE}

​ 于是得出：SAPCSABC=PDBE=FGBE\frac{S_{APC}}{S_{ABC}} = \frac{PD}{BE} = \frac{FG}{BE}

又因为 △AFG\triangle AFG 和 △ABE\triangle ABE是相似三角形（为什么就不用多说了，初中知识），所以FGBE=AFAB\frac{FG}{BE} = \frac{AF}{AB}

这时候，结合开头提到的公式：AP⃗=βAB⃗+γAC⃗\vec{AP} = \beta\vec{AB} + \gamma\vec{AC}，然后再结合向量加法的几何理解，我们可以得到AF=β∗ABAF = \beta * AB，从而得到AFAB=β\frac{AF}{AB} = \beta，也就得到了β=SAPCSABC\beta = \frac{S_{APC}}{S_{ABC}}

（6）同理。我们也可以得到 α\alpha 和 γ\gamma 的值，如下：

α=SBPCSABCβ=SAPCSABCγ=SAPBSABC\alpha = \frac{S_{BPC}}{S_{ABC}}\\ \beta = \frac{S_{APC}}{S_{ABC}}\\ \gamma = \frac{S_{APB}}{S_{ABC}}\\

（7）至于三角形的公式，咱们不多说，这里贴出来：

SBPC=0.5∗∣∣PB⃗×PC⃗∣∣SAPC=0.5∗∣∣PA⃗×PC⃗∣∣SAPB=0.5∗∣∣PA⃗×PB⃗∣∣SABC=0.5∗∣∣AB⃗×AC⃗∣∣S_{BPC} = 0.5 *||\vec{PB} \times \vec{PC}||\\ S_{APC} = 0.5 *||\vec{PA} \times \vec{PC}||\\ S_{APB} = 0.5 *||\vec{PA} \times \vec{PB}||\\ S_{ABC} = 0.5 *||\vec{AB} \times \vec{AC}||\\

大功告成，希望对大家所有帮助！画图用的是在线软件：geogebra

结尾

喜欢的小伙伴可以点点关注+赞哦！谢谢大家！

希望对各位小伙伴能够有所帮助哦，永远在学习的道路上伴你而行， 我是航火火，火一般的男人！

avatar
文章
阅读
粉丝