
theme: fancy
大家好,间隔快一个月没有发文章了,主要是这一篇推导实在是超出我能力范围太多了,同时缺乏相关的资料,啃下来非常不容易。 本文的亮点有
- 小白也能读懂: 笔者十余年没用过数学,就是一个初中生数学水平,在理解过程中,看到资料中的有很多因为所以,完全不明白为什么可以因为所以: ( 原因是很多公式定理我都忘了,或者不知道。通过不断的查阅资料,终于写出来整个推导过程,这篇文章补充了很多这种基础知识,我相信这篇文章也会适合小白阅读,因为我自己就是小白
- 图例标记,证明符号,代码变量一致: 在初次看贝塞尔曲线的距离场代码,完全搞不明白这个代码是怎么写出来的。再后来找到一些资料里面有整个证明过程,也看不懂。很大一部份原因是代码和数学公式中的符号完全不一样,本文图例,证明,代码 所有符号都是一样
- 用棣莫弗定理和费马引理带图证明了第三个根不可能为最小值
- 关于贝塞尔曲线的SD推导,没有发现很完整的英文资料,更别说中文资料了...
基础
以下公式作为索引,会在推导过程中用到。如果这里讲的不明白,可以wiki查看。 嫌麻烦可以直接跳转到
推导
链式法则求导
链式法则是一种在微积分中求导复合函数的基本规则。
dxdf(g(x))=f′(g(x))⋅g′(x)
多项式求导
多项式求导是微积分中的一个基本概念,
P(x)=anxn+an−1xn−1+⋯+a2x2+a1x+a0
其中, an,an−1,…,a1,a0 是常数系数, n 是最高次幂且是一个非负整数。
多项式函数的导数 P′(x) 可以通过下列规则来计算:
- 幂规则:如果 f(x)=xn ,其中 n 是任意实数,则 f′(x)=n⋅xn−1 。
- 常数规则:如果 C 是一个常数, f(x)=C 的导数是 0。即 C′=0 。
三次单位根
三次单位根,又被称为立方根的单位根,是复数中的一种特殊类型的数,它们是方程 x3=1 的解。
x1x2x3=1=e3i2π=cos32π+isin32π=−21+i23=e3i2π⋅2=cos34π+isin34π=−21−i23
三倍角公式
三倍角公式是三角函数中的一个重要公式,它将三倍角的三角函数值与单角的三角函数值联系起来。
cos(3A)=4cos3A−3cosA
欧拉公式
这个关系式在复分析中非常关键,它将复数的指数运算和三角函数联系起来。
eiθ=cosθ+isinθ
棣莫弗定理
当我们求一个复数 z 的 n 次根时,结果可以表示为
z1/n=r1/n(cos(nθ+2kπ)+isin(nθ+2kπ)),k=0,1,…,n−1
卡丹方程
方程形如 x3+px+q=0,它没有二次项,该形式的方程称为“折减形式”(Depressed form)或“卡丹形式”
其根由以下公式给出:
x=3−2q+(2q)2+(3p)3+3−2q−(2q)2+(3p)3
为了应用卡丹方程,任意形式的三次方程 ax3+bx2+cx+d=0 需要首先通过代换转化为折减形式。这通常是通过对 x 进行替换,使原方程中的二次项消失,即设
x=y−3ab
使用卡丹方法时,我们通常会碰到一个名为“卡丹判别式”的量
Δ=(2q)2+(3p)3
这个量告诉我们方程的根的性质:
- 如果 Δ>0,则方程有一个实根和两个复数根。
- 如果 Δ=0,则所有根都是实数,并且至少有两个根相等。
- 如果 Δ<0,则方程有三个不同的实数根。
韦达定理
韦达定理(Viète's formulas),是关于多项式方程根与其系数之间关系的一组定理。这些定理对于任何实数或复数系数的多项式方程都成立。
anxn+an−1xn−1+⋯+a1x+a0=0⇓x1+x2+⋯+xn=−anan−1x1x2+x1x3+⋯+xn−1xn=anan−2x1x2…xn=(−1)nana0
费马引理
费马引理(Fermat's Lemma)是微积分学中的一个基本结果,引理表述如下:
如果函数 f 在点 x=c 取得局部极大值或局部极小值,并且如果 f 在 x=c 可导,那么 f′(c)=0
费马引理仅仅给出了可导函数在某个点为极值的必要条件。也就是说,有些驻点可以不是极值点,它们是拐点。要想知道一个驻点是不是极值点,并进一步区分极大值点和极小值点,我们需要分析二阶导数(如果它存在)。当该点的二阶导数大于零时,该点为极小值点;当该点的二阶导数小于零时,该点为极大值点。若二阶导数为零,则无法用该法判断,需列表判断。
推导
二阶贝塞尔曲线函数
 贝塞尔曲线是线性插值的结果。如果我们知道两点之间的距离,并想找出离第一个点20%间距的一个新的点(也就是离第二个点80%的间距),我们可以通过简单的计算来得到:
贝塞尔曲线是线性插值的结果。如果我们知道两点之间的距离,并想找出离第一个点20%间距的一个新的点(也就是离第二个点80%的间距),我们可以通过简单的计算来得到:
Givenp1=somepointp2=otherpointdistance=(p2−p1)ratio=100percentage,our new point =p1+distance⋅ratio
2D坐标系中有A,B,C 三个点, 有变量t, t的取值[0,1]。 以此绘制一条2阶贝塞尔曲线, 对坐标中任意点p, 求p到该曲线的最短距离
vec2 Bezier(vec2 a, vec2 b, vec2 c, float t) {
return mix(mix(a, b, t), mix(b,c,t), t);
}
又有
mix(a,b,t)=a⋅(1−t)+b⋅t
用数学公式表达,可以获取
P(t)=(1−t)2⋅A+2⋅(1−t)⋅t⋅B+t2⋅C=(1−2t+t2)⋅A+(2t−2t2)⋅B+t2⋅C letf(t)=P(t)−p f(t)=(A−2B+C)⋅t2+2⋅(B−A)⋅t+A−p let⎩⎨⎧a=B−Ab=A−2∗B+Cc=2∗(B−A)=2ad=A−p⟹f(t)=b⋅t2+c⋅t+d
最小距离就是求极值
于是贝塞尔曲线距离场问题变成了
what value t,the minimum value of ∣f(t)∣
这个问题等于
what value t,the minimum value of f(t)2
于是这就变成了一个求极值的问题,极值点一定是导数为0的点
根据链式法则求导,可以计算如下:
dtd[f(t)]2=2f(t)⋅f′(t)
应用基本的多项式求导
0=2f(t)⋅f′(t)=2⋅(b⋅t2+c⋅t+d)⋅(2b⋅t+c)=b⋅t2⋅(2b⋅t+c)+c⋅t⋅(2b⋅t+c)+d⋅(2b⋅t+c)=(b⋅t2⋅2b⋅t)+(b⋅t2⋅c)+(c⋅t⋅2b⋅t)+(c⋅t⋅c)+(d⋅2b⋅t)+(d⋅c)=2b2⋅t3+bc⋅t2+2bc⋅t2+c2⋅t+2bd⋅t+dc=2b2⋅t3+3bc⋅t2+(c2+2bd)⋅t+dc
最后的问题变成了一个3次多项式求解的问题......
g(t)=2b2⋅t3+3bc⋅t2+(c2+2bd)⋅t+dc
卡丹方程解三次多项式
0=2b2⋅t3+3bc⋅t2+(c2+2bd)⋅t+dc=t3+b23ab⋅t2+b22a2+bd⋅t+b2da
let a2=b23aba1=b22a2+bda0=b2da⟹x3+a2x2+a1x+a0=0
求二阶导找出拐点,平移导0处(换元) 可以消除掉2次项
f(x)=x3+a2x2+a1x+a0x→x−3a2⟹f′′(x)=6x+2a2=0⟹x3+a1x+a0=0
在掏出卡丹公式中的p q
let{p=−3a1q=−2a0⟹x3=3px+2q
let x→s+t⟹x3=3st(s+t)+s3+t3⟹x3=3st⋅x+s3+t3
将上述方程写成以下形式将等式1与2对比系数可得
{s3⋅t3=p3s3+t3=2q
根据韦达定理, s3 t3 为等式 x2−2qx+p3=0的解,于是有
{s3=q+q2−p3t3=q−q2−p3
将等式完全展开,可以得到
x=s+t=3q+q2−p3+3q−q2−p3
这套用三次单位根便可以完全展开
⟹x=⎩⎨⎧3q+q2−p3+3q−q2−p3ω3q+q2−p3+ω23q−q2−p3ω23q+q2−p3+ω3q−q2−p3ω=e32πi=−21+23i
这个解法存在的问题是,只有依次计算每一个公式才能知道那些根实根
三角换元解三次多项式
采用这种方法能够规避上面的根号,以及实根不确定的问题
依三倍角公式有
cos(3θ)=4cos3θ−3cosθ
同样**这是一个三次方程,**所以如果存在以下的三次方程,可以得出
4x3−3x−cos3θ=0⟹x=cosθ
还记得我们上一节等式1
x3=3px+2q
如果使用换元,让等式1能够满足三倍角公式,可以直接得出答案
x=2p C⟹4C3−3C=ppq=cos3θ⟹x=2pcos(3ϕ+2kπ),ϕ=arccos(ppq),k=0,1,2
这个解是代码中使用的方法
复平面极坐标解三次多项式
回到我们的等式
{s3=q+q2−p3t3=q−q2−p3
考虑三个实数根的情况q2<p3,如果q2<p3, s3和 t3为一对共轭复数
s3=q+p3−q2i
s3的magnitude r为
q2+p3−q2=pp
将s^3$$t^3放到极坐标可以得到下面这个图

对s3开立方根,利用棣莫弗定理公式可得
z1/3=r1/3(cos(3ϕ+2kπ)+isin(3ϕ+2kπ)),k=0,1,…,n−1
直接就得到了三个解

对于解0
x=s0+t0=2RealPart(s0)=2p cos(ϕ/3)
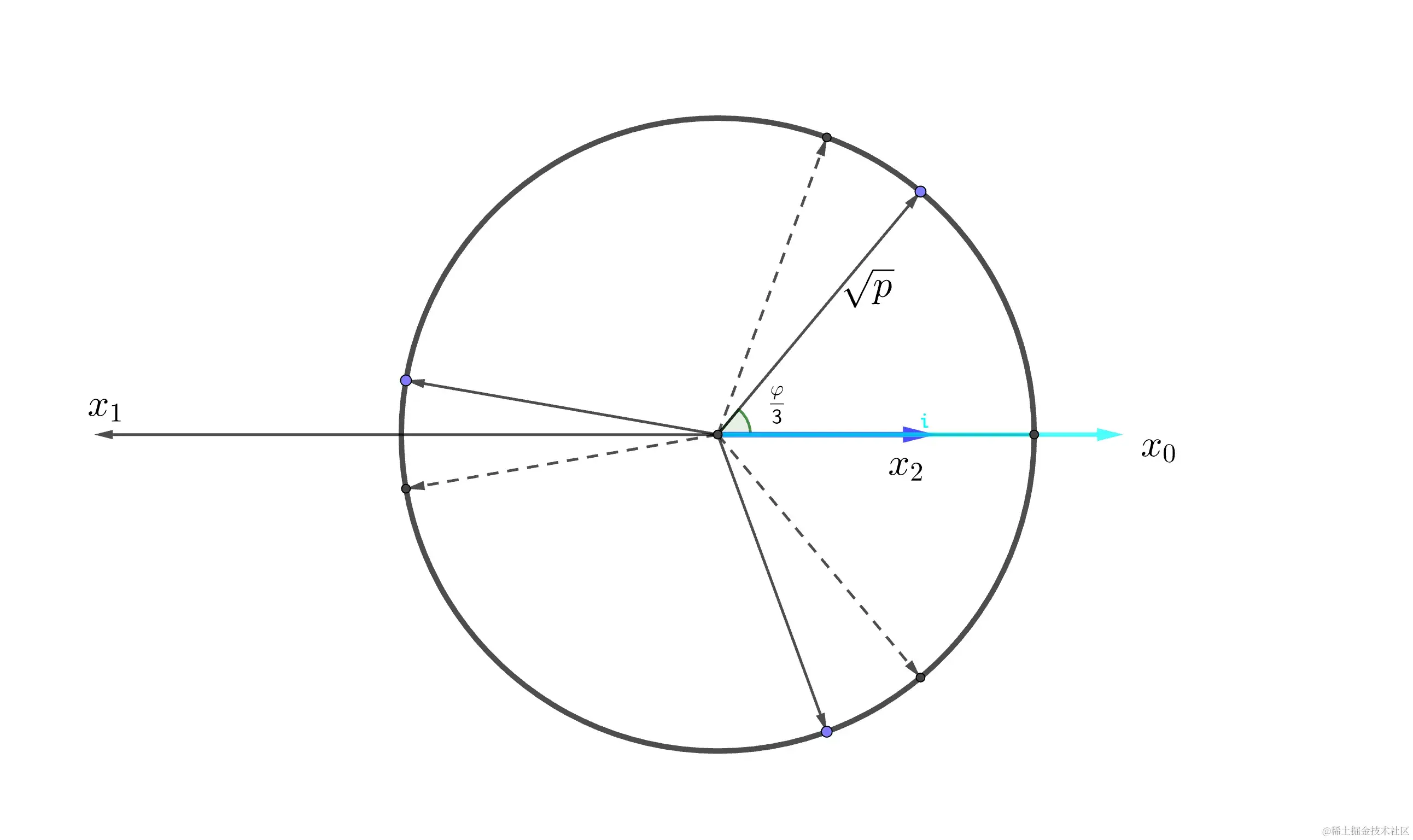
将s+t在极坐标复平台进行向量求和,于是我们得到与上一节一模一样的答案!!!而着背后其实就是欧拉公式
x=2pcos(3ϕ+2kπ),ϕ=arccos(ppq)k=0,1,2
证明极小值只能在t0和t1中
我们这里回到用t表示最终根的结果
ϕ∈[0,π]⟹3ϕ=θ∈[0,3π]
geogebra: www.geogebra.org/classic/u8u…
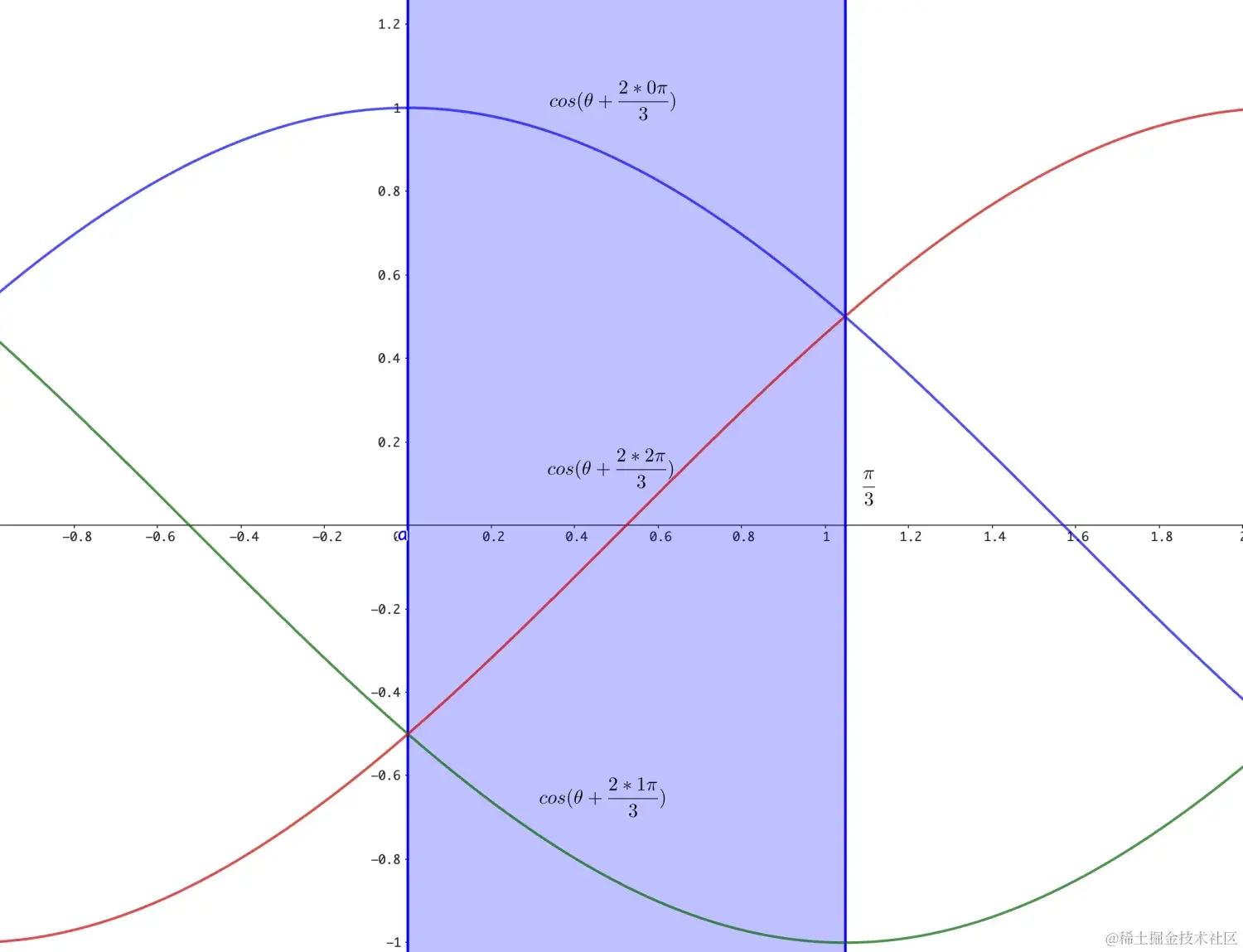
对于任意θ∈[0,3π], 都有
cos(θ+32∗1π)<cos(3ϕ+2∗2π)<cos(32∗0π)⟹t1<t2<t0
回到二阶贝塞尔曲线的函数,有
f(t)dtd[f(t)]2=g(t)g′(t)=b⋅t2+c⋅t+d=2b2⋅t3+3bc⋅t2+(c2+2bd)⋅t+dc=6b2∗t2+6bc∗t+c2+2bd
f(t)2的极值点一定是在一阶导数g(t)=0的3个根,即t_1$$t_2$$t_0。 如果有三个实根的只有以下两种图像
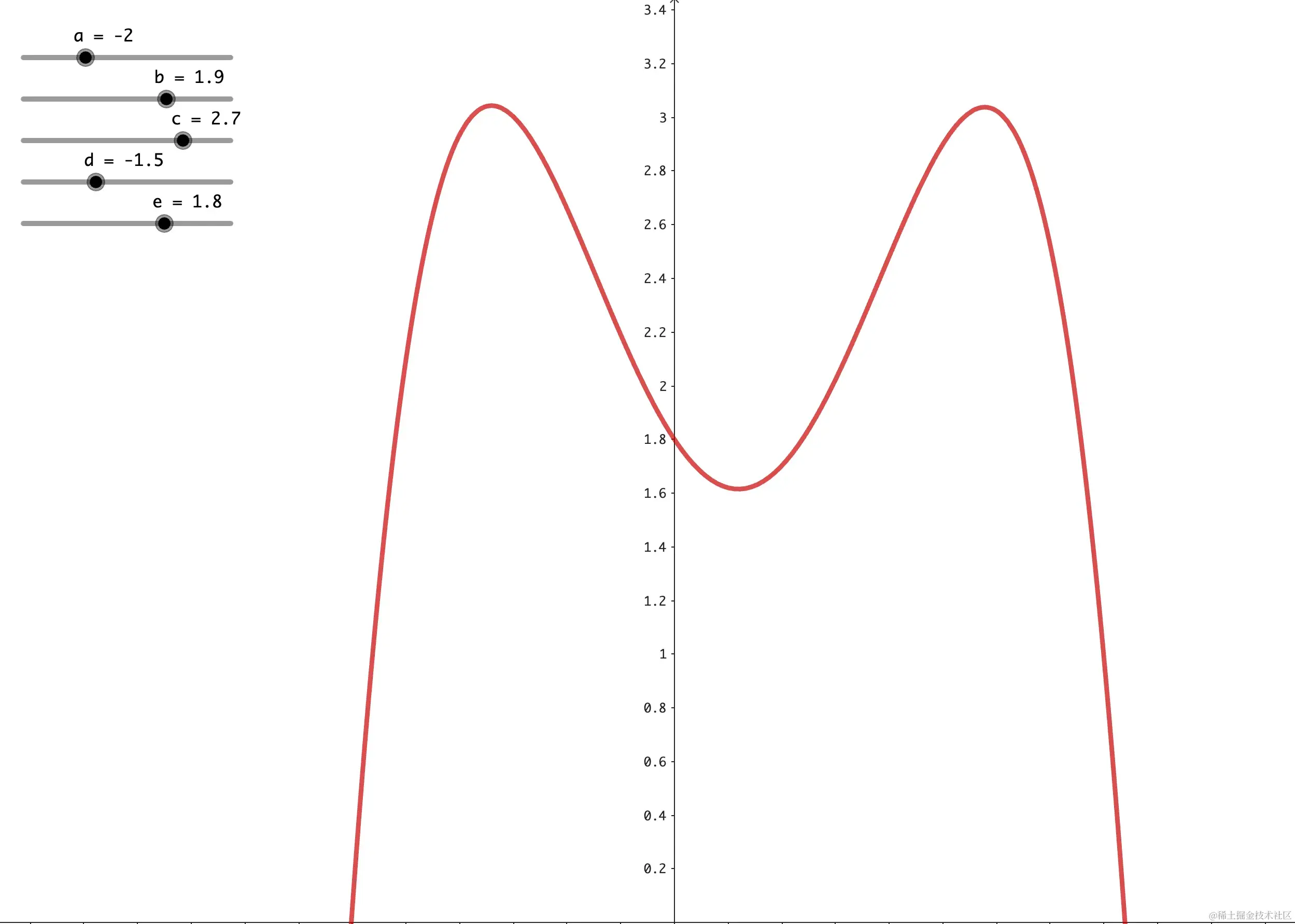

geogebra: www.geogebra.org/classic/qdr…
- 在t0和 t1有极大值,同时t2为极小值
- 在t0和 t1有极小值,同时t2为极大值
以上两个函数的二阶导数g′(t)的图像分别为以下两种,分别开口朝上和开口朝下
由于
g′(t)=6b2∗t2+6bc∗t+c2+2bd 中 6t2>0,
所以函数图像开口朝上,且有
t1<t2<t0
从图像观察可以得出
g′(t2)<max(g′(t0),g′(t1))(1)
假设现在处于情况1 在t0和t1有极大值,同时t2为极小值。 那么根据费马引理有 极大值的二阶导数<0有
g′(t0)<0 and g′(t1)<0(2)
极小值的二阶导数>0 有
g′(t2)>0(3)
由不等式1,2可以推出
g′(t2)<max(g′(t0),g′(t1))<0(4)
不等式3,4矛盾,故情况1不存在。
贝塞尔曲线的最近距离一定是在根t0 t1 中
贝塞尔曲线是线性插值的结果。如果我们知道两点之间的距离,并想找出离第一个点20%间距的一个新的点(也就是离第二个点80%的间距),我们可以通过简单的计算来得到: