深度强化学习（DRL）算法附录 2 —— 策略迭代和价值迭代马尔可夫决策过程（MDP）马尔可夫链（具有马尔可夫性质的

马尔可夫决策过程（MDP）

马尔可夫链（具有马尔可夫性质的随机过程）+ A（动作：会导致状态转移） + R（奖励：衡量动作的好坏）

动态特性

定义如下概率：

$p(s^{\prime}, r | s, a) \triangleq {P}({S_{t+1}=s^{\prime}, R_{t+1}=r | S_t=s, A_t=a})$

那么状态转移概率（系统自身）：

$p(s^{\prime} |s, a)=\sum_{r \in R} p(s, r | s, a)$

策略表示（Policy)

策略： $\pi$

确定性策略： $a\triangleq \pi(s)$

随机性策略： $\pi(a|s)\triangleq P(A_t = a | S_t = s)$

回报

用来评估在 $s_t$ 时刻的策略的好坏，我们定义在 $s_t$ 时刻的回报为：

$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^{2} R_{t+3} + ... , \gamma \in [0,1]$

价值函数

回报的期望就是价值函数，通俗的说就是回报的平均数（因为从 s 出发的路径会像树枝一样散开） state-value: $v_\pi(s) = E[G_t∣S_t=s]$

action-value: $q_\pi(s,a) = E[G_t | S_t=s, A_t = a]$

state-value 和 action-value 的关系： $v_\pi(s) = \sum_a \pi(a \mid s) q_\pi(s, a)$ (如果 $\pi$ 是确定性策略，两个值相等) (1)

$q_\pi(s, a) = \sum_{r, s'}p(s', r | s, a)[r + \gamma v_\pi(s')]$ (2)

贝尔曼期望方程

即把（2）带入（1），把（1）带入（2）产生的两个等式得到 v(s) 和 v(s‘）以及 q(s,a) 和 q(s', a') 的关系，这就是贝尔曼方程的核心思想。

贝尔曼最优方程

最优价值函数：

$v_{*} \triangleq max_\pi v_\pi(s)$

$q_{*}(s,a) \triangleq max_\pi q_\pi(s,a)$

最优策略： $\pi_* \triangleq argmax_\pi v_\pi(s)$ = $argmax_{\pi}q_\pi(s,a)$ 由（1）（2）知：

$v_* = max_\pi q_\pi(s,a)$ （3）

$q_* = \sum_{r, s'}p(s', r | s, a)[r + \gamma v_*(s')]$ (这里不能把求和替换成 max 的原因是，我们只能让 v* 最优，因为 p 由系统决定，我们无法决定）（4）即把（3）带入（4），把（4）带入（3）产生的两个等式和贝尔曼方程一样，得到 v*(s) 和 v*(s‘）以及 q*(s,a) 和 q*(s', a') 的关系，这就是贝尔曼最优方程的核心思想。

策略迭代

在 MDP 已知的情况下

策略评估（PE）

知道 pi，我们需要评估出对应的 v 和 q 值。

解析解使用线性代数的方式解线性方程组：V = R + $\gamma$ P V
迭代解因为贝尔曼期望方程是不动点方程，所以可以迭代求解。 vk -> vk+1，k-> $\infty$ ，一直迭代下去，可以收敛。

策略改进（PI）

根据 v 和 q ，我们构造出 pi' 优于 pi。

策略改进定理给定 pi,pi'，如果 $\forall s \in S$ ，有 $q(s, \pi'(s)) \geq v_\pi(s)$ ，那么则有 $∀s∈S$ ， $v_{\pi'}(s) \geq v_{\pi}(s)$ 。
贪心策略 $\pi'(s) = argmax_a q_\pi(s,a)$ （满足策略改进定理）所以 pi -> PE -> q（或者 v） -> PI -> pi' 一直循环下去，就可以得到 v*。

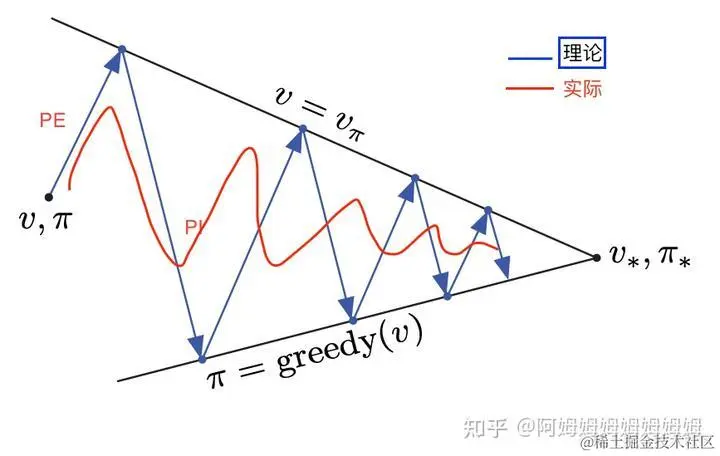
价值迭代

PE 只进行一步的策略迭代。

异步价值迭代

PE 和 PI 不是先后顺序，比如 V 里面的一个值更新了一步，没有等到其他 v 更新，就直接进行 PI 了。

深度强化学习（DRL）算法 附录 2 —— 策略迭代和价值迭代