贝叶斯公式由英国数学家贝叶斯发展而来，在统计学和概率论中有着广泛的应用。
与传统的先验概率不同，它提出的后验概率方式，会根据不断出现的新证据来更新概率估计，
从而使得估计的准确性能够不断改善。

本文尝试通过一个简单的预测天气的示例来讲解后验概率是怎么回事，以及如何根据它推导出贝叶斯公式的。

1. 从预测天气开始

这里为了简化，我们只考虑两种天气情况，晴天和雨天。
在没有其他条件的情况下，我们预测明天的天气，得到的是 50%概率是晴天，50%概率是雨天。

这个概率也可称为先验概率，就像扔硬币一样，
没有其他条件的情况下，我们根据经验，可得出硬币落地后正反面的概率各为 50%。
上面的天气预测结果，绘制成概率图如下（晴天雨天的概率各占50%）：

根据上面的情况，可以整理成简单的公式如下：
$P(天气=晴天)=0.5$
$P(天气=雨天)=0.5$
其中，$P(...)$表示某个事件的概率。

2. 引入新变量

接着上面的示例讨论，为了更精确的预测明天的天气，我们引入新的变量。
假设这个新的变量霞光，也就是当天是否有朝霞和晚霞。
这里为了简化，假设朝霞和晚霞必然出现，且不会同一天出现。

根据谚语“朝霞不出门，晚霞行千里”，
我们假定明天晴天的话，今天晚霞的概率为80%，朝霞的概率为20%。
明天雨天的话，今天晚霞的概率为10%，朝霞的概率为90%。

整理成概率的表格更直观一些：

明天天气	朝霞	晚霞
晴天	0.2	0.8
雨天	0.9	0.1

这个表格是按行来看的，表示不同天气情况下，朝霞和晚霞出现的概率。
用公式来表示的话：
$P(霞光=朝霞 | 天气=晴天) = 0.2$ 这个公式表示明天晴天的话，今天朝霞的概率 20%
也就是 $P(A|B)$ 表示B发生时，A发生的概率。

同理可得出：
$\begin{cases} \quad P(霞光=晚霞 | 天气=晴天) = 0.8 \\ \quad P(霞光=朝霞 | 天气=雨天) = 0.9 \\ \quad P(霞光=晚霞 | 天气=雨天) = 0.1 \end{cases}$

3. 联合概率

现在，我们有2个变量了，霞光和天气。
根据这两个变量，可以计算它们同时发生的概率，也就是联合概率。
联合概率的公式用 $P(A, B)$来表示，事件A和事件B之间用逗号。

根据上一节的表格，绘制联合概率分布图如下：

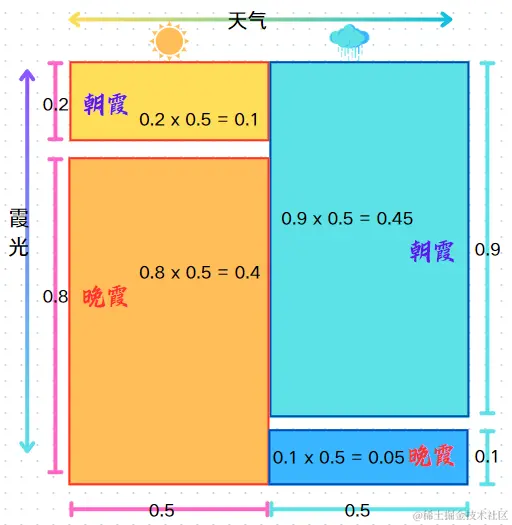
由上文第一节的假设可知：$P(晴天)=0.5$，$P(雨天)=0.5$
由上文第二节的内容可知：
$P(晚霞|晴天)=0.8$，$P(朝霞|晴天)=0.2$
$P(晚霞|雨天)=0.9$，$P(朝霞|雨天)=0.1$

所以得出上图中各个部分联合概率的结果如下：
$\begin{cases} \quad P(霞光=朝霞,天气=晴天) = P(朝霞|晴天)\times P(晴天) = 0.1 \\ \quad P(霞光=晚霞,天气=晴天) = P(晚霞|晴天)\times P(晴天) = 0.4 \\ \quad P(霞光=朝霞,天气=雨天) = P(朝霞|雨天)\times P(雨天) = 0.45 \\ \quad P(霞光=晚霞,天气=雨天) = P(晚霞|雨天)\times P(雨天) = 0.05 \end{cases}$
从公式可以算出，符合谚语“朝霞不出门，晚霞行千里”的概率高达85%，即：
$P(霞光=朝霞,天气=雨天) + P(霞光=晚霞,天气=晴天) = 0.45+0.4=0.85$

4. 推导贝叶斯

接下来，就可以开始推导贝叶斯公式了，
为了简化公式，我们假设上面的变量霞光为A，天气为B，
则$A$表示朝霞或晚霞中的一种；$B$表示晴天或雨天中的一种。

那么，上一节的4个联合概率公式可简化为：$P(A, B) = P(A|B) \times P(B) \quad (1)$
或者简化为：$P(B,A) = P(B|A) \times P(A) \quad (2)$

$P(A, B)$和 $P(B,A)$都是表示同样的含义，也就是$A$和$B$同时发生的概率。
所以上式$(1)$和$(2)$是相等的，从而得出：
$P(A|B) \times P(B) = P(B|A) \times P(A)$
即：$P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}$或$P(B|A)=\frac{P(A|B) \times P(B)}{P(A)}$
这就是贝叶斯公式。

5. 后验概率

最后，我们来看看什么是后验概率，以及贝叶斯公式为什么是后验概率。

提到后验概率，不得不提先验概率，
所谓先验概率，就是事件发生时，我们已经能够判断出事件发生的概率，
判断的依据就是先前的经验，所以被成为先验概率。
比如，扔硬币，掷筛子，买彩票等等。
扔硬币之前，我们就已经可以判断正反面的概率各为 50%；
掷筛子之前，可以判断掷出任意点数的概率均为33.33%；
买彩票之前，也可以算出连续猜对几个数字的概率。

这些都是先验概率，平时生活中，我们做各种决策时，常常都在不知不觉中使用先验概率来判断。
然而，对于复杂的情形，先验概率的准确性大大降低，就以本文中的天气预测为例，
天气预测涉及很多因素，不仅仅是上文的朝霞晚霞，还有不同的经纬度，气温，湿度，风向等等都对明天的天气有影响。

如果用先验概率的做法，我们会根据历史数据来算出各个因素（包括朝霞晚霞，经纬度，气温，湿度，风向等等）对明天天气的影响，然后生成一个分类模型。
然后通过这个分类模型预测明天的天气，就是先验概率。

不过，天气不像扔硬币，掷筛子，买彩票那样一成不变，随着时间的推移，我们的环境在不断变化（包含人为的和非人为的）。
所以根据历史数据计算出的预测模型随着时间推移会越来越不准确。

这时就需要通过后验概率来更新各个因素（包括朝霞晚霞，经纬度，气温，湿度，风向等等）对明天天气的影响，
然后更新我们的分类模型，更新的方式就是贝叶斯公式，

假设各个影响天气预测的因素分别为$A_1, A_2, A_3...A_n$，$B$表示实际天气情况。
拓展上一节中的贝叶斯公式，可得：$P(A_1,A_2...A_n|B) = \frac{P(B|A_1,A_2...A_n) \times P(A_1,A_2...A_n)}{P(B)}$
根据这个公式，可以反推出$P(A_1,A_2...A_n|B)$，即在已知天气$B$的情况下，各个影响天气的因素出现的概率。
这个概率就是用来更新天气预测模型用的。

总的来说，后验概率可以看做先验概率的一个补充，它以先验概率为基础，根据不断出现的新证据或新数据，对先验概率的进行更新。
这个过程和机器学习的过程非常类似，所以贝叶斯概率也是机器学习中分类模型常用的算法。