冒泡排序
排序思路:
1.比较相邻的2个数,不符合要求则替换位置,每比较一轮
n-1次将最大或最小的数冒泡到最顶端,共比较n-1轮,时间复杂度=O(n-1)(n-1)=O(n2)。由于满足规则才需要替换位置,对于相等元素来说相对位置不变,所以是
稳定排序
图解
算法实现
function bubbleSort(arr) {
for (let i = 1; i < arr.length; i++) {
for (let j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j + 1], arr[j]] = [arr[j], arr[j + 1]]
}
}
}
return arr;
}
选择排序
排序思路:
1.从数组首或尾选择一个基准用于填充最小值<或最大值>,遍历其他未排序的值,选择最小或最大值依次填充。需要填充的个数为
n-1,每次填充平均需要遍历的个数为n/2。时间复杂度=O(n-1)*(n/2)=O(n2)。2.由于遇到相等元素后,元素顺序会发生改变,所以是
不稳定排序。举个例子:[5a, 2, 5b, 1]进行排序,第一轮排序到排序完成完:[1,2,5b,5a]。2个5的相对位置发生了改变。
图解
算法实现
function selectSort(arr) {
for (let i = 0; i < arr.length; i++) {
let min = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
[arr[i], arr[min]] = [arr[min], arr[i]]
}
}
插入排序
排序思路:
1.将元素分为已排序与未排序两类,将未排序第一个元素插入已排序元素完成排序。已排序元素寻找插入位置,最坏的情况需要寻找n/2次,未排序元素个数为n-1。时间复杂度=O(n-1)(n/2)=O(n2)
2.由于遇到相等元素后,元素将进行插入操,相对元素的位置未发生改变,所以是
稳定排序。
图解
算法实现
function selectSort(arr) {
for (let i = 0; i < arr.length; i++) {
let min = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
[arr[i], arr[min]] = [arr[min], arr[i]]
}
}
计数排序
排序思路:
1.空间换时间。需要遍历一次获取数组中最大最小值,计算区间范围,并为其开辟计数空间。再次遍历,将数值映射为下标,并统计个数。最后将统计格式进行转换。由于是线性查找,时间复杂度O(n)
2.由于计数排序不是基于比较的。元素已经不是原来的元素,所以是
不稳定排序。
图解
 算法实现
算法实现
function countSort(arr) {
const [min, max] = [Math.min(...arr), Math.max(...arr)]
let res = new Array(max - min + 1).fill(0);
for (let i = 0; i < arr.length; i++) {
res[arr[i] - min]++
}
res = res.map((num, index) => {
return new Array(num).fill(index + min)
})
arr = res.flat(1)
return arr
}
快速排序
排序思路:
1.选择一个基准,将数组中大于基准的值放到右边,小于基准的放到左边,然后再将基准放到中间。然后递归遍历左右两侧的数组。在最好的情况下,所以数据都能被平分,树的深度达到log(n),需要确定数据个数为n,复杂度=O(nlogn)
2.由于基准可能会越过相等元素到中心位置。所以是
不稳定排序。
图解
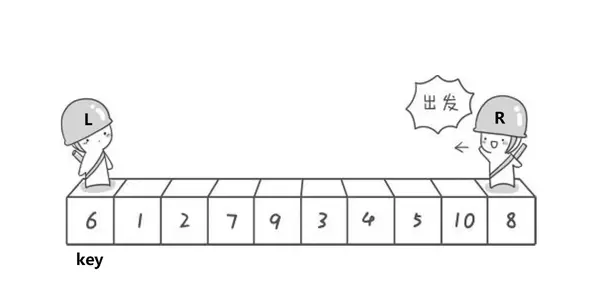
算法实现
function quickSort(arr, start = 0, end = arr.length - 1) {
if (start >= end) {
return start;
}
const base = arr[start]
while (start < end) {
while (start < end && arr[end] >= base) {
end--
continue;
}
arr[start] = arr[end]
while (start < end && arr[start] <= base) {
start++
continue;
}
arr[end] = arr[start]
}
arr[start] = base;
quickSort(arr, 0, start - 1)
quickSort(arr, start + 1, end)
}