Leecode Hot100 刷题笔记本-贪心算法（C++版）

1. 53. 最大子数组和 中等
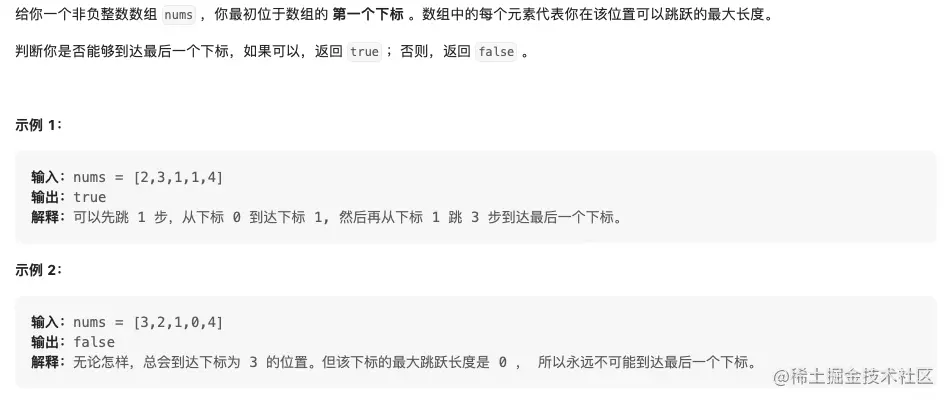
2. 55. 跳跃游戏 中等
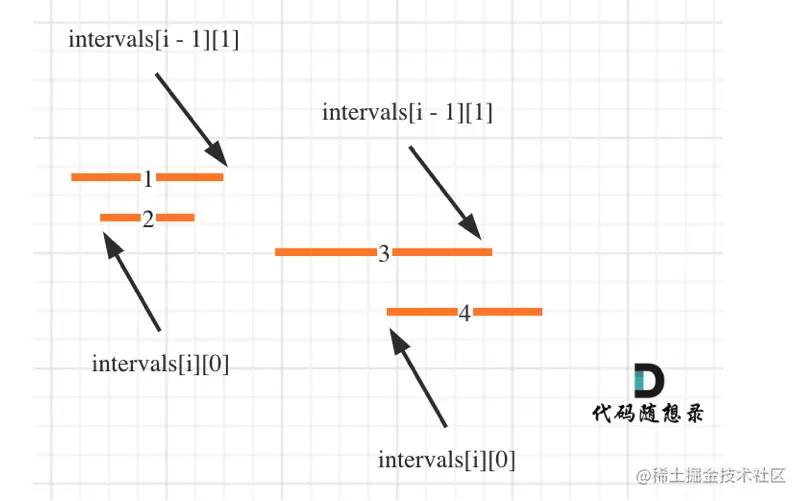
3. 56. 合并区间 中等
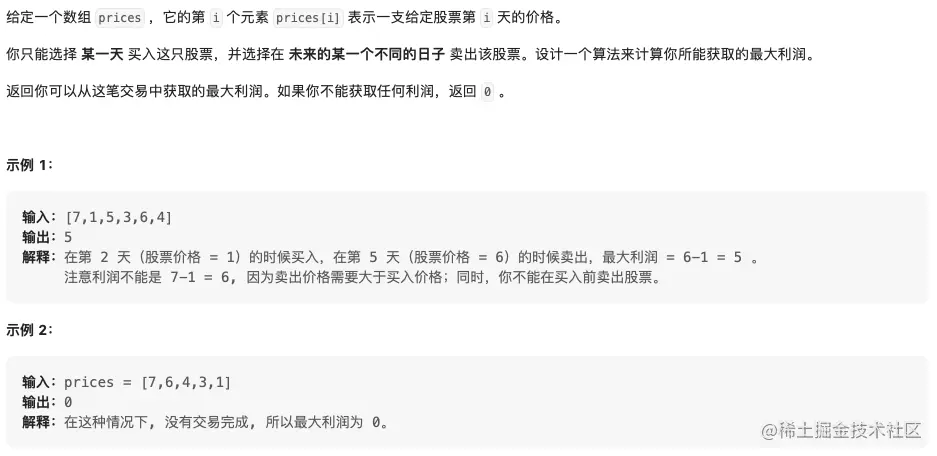
4. 121. 买卖股票的最佳时机 简单

53. 最大子数组和

解法1: 动态规划

• 动态规划的是首先对数组进行遍历，当前最大连续子序列和为 sum，结果为 ans

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = 0;
        int ans = nums[0];
        for (const auto &x: nums) {
            sum = max(sum + x, x);
            ans = max(ans, sum);
        }
        return ans;
    }
};

• 时间复杂度: O(n)，其中 n 为 nums 数组的长度。我们只需要遍历一遍数组即可求得答案
• 空间复杂度: O(1)。我们只需要常数空间存放若干变量

解法2: 贪心算法

• 从左向右迭代, 一个个数字加过去，如果sum<0, 重新开始找子序串

class Solution
{
public:
    int maxSubArray(vector<int> &nums)
    {
        //类似寻找最大最小值的题目，初始值一定要定义成理论上的最小最大值
        int result = INT_MIN;
        int numsSize = int(nums.size());
        int sum = 0;
        for (int i = 0; i < numsSize; i++)
        {
            sum += nums[i];
            result = max(result, sum);
            //如果sum < 0，重新开始找子序串
            if (sum < 0)
            {
                sum = 0;
            }
        }

        return result;
    }
};

• 时间复杂度: O(n)，其中 n 为 nums 数组的长度。我们只需要遍历一遍数组即可求得答案
• 空间复杂度: O(1)。我们只需要常数空间存放若干变量

解法3: 分治算法

• 取数组中心点为中心, 最大子序要么全在中心左边, 要么全在右边, 要么跨中心
• 跨中心的情况分治成中心点左侧和右侧的最大子序和问题

class Solution
{
public:
    int maxSubArray(vector<int> &nums)
    {
        //类似寻找最大最小值的题目，初始值一定要定义成理论上的最小最大值
        int result = INT_MIN;
        int numsSize = int(nums.size());
        result = maxSubArrayHelper(nums, 0, numsSize - 1);
        return result;
    }

    int maxSubArrayHelper(vector<int> &nums, int left, int right)
    {
        if (left == right)
        {
            return nums[left];
        }
        int mid = (left + right) / 2;
        int leftSum = maxSubArrayHelper(nums, left, mid);
        //注意这里应是mid + 1，否则left + 1 = right时，会无线循环
        int rightSum = maxSubArrayHelper(nums, mid + 1, right);
        int midSum = findMaxCrossingSubarray(nums, left, mid, right);
        int result = max(leftSum, rightSum);
        result = max(result, midSum);
        return result;
    }

    int findMaxCrossingSubarray(vector<int> &nums, int left, int mid, int right)
    {
        int leftSum = INT_MIN;
        int sum = 0;
        for (int i = mid; i >= left; i--)
        {
            sum += nums[i];
            leftSum = max(leftSum, sum);
        }

        int rightSum = INT_MIN;
        sum = 0;
        //注意这里i = mid + 1，避免重复用到nums[i]
        for (int i = mid + 1; i <= right; i++)
        {
            sum += nums[i];
            rightSum = max(rightSum, sum);
        }
        return (leftSum + rightSum);
    }
};

• 时间复杂度为O(nlogn)
• 空间复杂度为O(logn)

55. 跳跃游戏

解法1: 贪心算法

• 逐个遍历数组中的元素
• 我们依次遍历数组中的每一个位置，并实时维护最远可以到达的位置。对于当前遍历到的位置 x，如果它在最远可以到达的位置的范围内，那么我们就可以从起点通过若干次跳跃到达该位置，因此我们可以用 x+nums[x] 更新 最远可以到达的位置
• rightmost = max(rightmost, i + nums[i])
• 如果 最远可以到达的位置 大于等于数组中的最后一个位置，那就说明最后一个位置可达，我们就可以直接返回 True 作为答案

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
};

• 时间复杂度为O(n)
• 空间复杂度为O(1)

56. 合并区间

解法1:贪心算法

• 用数组 merged 存储最终的答案
• 每次合并都取最大的右边界，这样就可以合并更多的区间了，整体最优：合并所有重叠的区间
• 如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界，则一定有重复

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) {
            return {};
        }
        sort(intervals.begin(), intervals.end());
        vector<vector<int>> merged;
        for (int i = 0; i < intervals.size(); ++i) {
            int L = intervals[i][0], R = intervals[i][1];
            if (!merged.size() || merged.back()[1] < L) {
                merged.push_back({L, R});
            }
            else {
                merged.back()[1] = max(merged.back()[1], R);
            }
        }
        return merged;
    }
};

• 时间复杂度为O(nlogn), 有一个快速排序
• 空间复杂度为O(1), 不算result数组（返回值所需容器占的空间）

121. 买卖股票的最佳时机

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int inf = 1e9;
        int minprice = inf, maxprofit = 0;
        for (int price: prices) {
            maxprofit = max(maxprofit, price - minprice);
            minprice = min(price, minprice);
        }
        return maxprofit;
    }
};

• 时间复杂度为O(n), 只需要遍历一次
• 空间复杂度为O(1), 只使用了常熟个变量