《Fundamentals of Computer Graphics》第五版 第十八章 颜色

濠水之鱼
139 阅读13分钟

颜色的研究涉及多个领域：光在空间中传播的物理，光与物质相互作用的化学，色彩感知的神经科学与心理学。图形学中，一般用遵从几何光学的能量波包——光子——来描述光在空间中的传播。光子的波长和能量之间满足如下关系：

λΔE=1239.9 nm⋅eV\lambda\Delta E = 1239.9\ \text{nm}\cdot\text{eV}

模拟单个光子的效率极低，因此图形学中通常同时模拟大量光子，并用光谱（spectrum）——能量或光子数与波长之间的关系——来描述。人眼能感知到的光波长大致在 380 nm380\ \text{nm} 到 800 nm800\ \text{nm} 之间。带光谱的射线追踪渲染器称为谱渲染器（spectral renderer）。但一般不会直接构造谱渲染器，而是用红绿蓝分量表示来代替光谱。

物体表面上光的行为通常用一个反射函数来模拟。反射函数是电子吸收光子并重新发射这一过程中所发生的化学的抽象，对于计算机图形学建模是有用的，但它没有对物理过程的解释性。光到达视网膜后会转化为电信号，进而传给大脑。颜色感知比表面上看起来复杂得多，它与光照、观测者有关，甚至会随着时间而变。除了反射光谱之外，颜色感知还与所处环境有关。颜色是视觉感知的一个方面，观察者可以通过颜色来区分两个相同形状大小的无结构视场之间的差异，比如，可能根据辐射能谱的差异来区分。

色度学（Colorimetry）

色度学是颜色测量与描述的科学。人类视网膜上感光细胞分为视杆细胞（rods）和视锥细胞（cones）。视杆细胞高度灵敏，在弱光条件下发挥作用。正常光照下，视锥细胞调节人类视觉。三种类型的视锥细胞一起决定了色觉。

直接记录视锥细胞的输出电信号具有侵入性，而且忽略了观测者之间有时存在的本质性差异。另一种方法是测量受试者对色块的响应，这导致了颜色匹配实验（color matching experiments），进行这种实验需要有一些标准化观测者，他们是实际人群的统计近似。

格拉斯曼定律（Grassmann’s Laws）

颜色匹配的实验定律可以总结为三原色通则（trichromatic generalization），即三个适当调制的颜色源的加法混合可以完全匹配上任何颜色刺激。Hermann Grassmann 最早描述了颜色匹配的代数法则，该法则被称为格拉斯曼加色匹配定律（Grassmann’s laws of additive color matching），用符号 ∼\sim 表示匹配，那么格拉斯曼定律可以总结为：

  • 对称律（Symmetry law），A∼B⇒B∼AA\sim B\Rightarrow B\sim A；
  • 传递律（Transitive law），A∼B、B∼C⇒A∼CA\sim B、B\sim C\Rightarrow A\sim C；
  • 正比律（Proportionality law），A∼B⇒αA∼αBA\sim B\Rightarrow \alpha A\sim \alpha B，其中 α>0\alpha>0；
  • 加法律（Additivity law），A∼B、C∼D⇒A+C∼B+DA\sim B、C\sim D\Rightarrow A+C\sim B+D。

加法律构成了颜色匹配、甚至整个色度学的基础。更严格地，上述匹配应该理解为光谱匹配，对称律、传递律，再结合显然成立的自反律可知，上述匹配 ∼\sim 是一种等价关系，颜色就是其等价类。而正比律和加法律则说明，颜色可根据代表元定义出数乘和加法：

αA‾=αA‾A‾+B‾=A+B‾\alpha\overline{A} = \overline{\alpha A} \\ \overline{A} + \overline{B} = \overline{A+B}

其中，A‾\overline{A} 是光谱 AA 所对应的等价类，即颜色。

视锥细胞响应（Cone Responses）

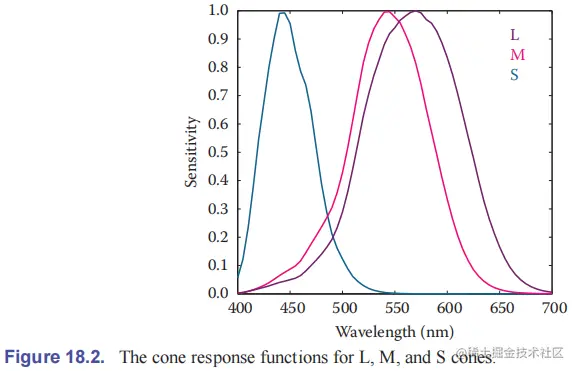
每种视锥细胞都只对某一波长范围灵敏，根据响应主峰的位置可以将视锥细胞分为三类：SS（short）、MM（medium）、LL（long）。视锥细胞的响应可以表示为输出电信号与输入波长之间的关系，三种视锥细胞响应函数（cone response function）分别记为：L(λ)L(\lambda)、M(λ)M(\lambda)、S(λ)S(\lambda)。对颜色刺激 Φ(λ)\Phi(\lambda) 的真实响应为：

L=∫λΦ(λ)L(λ)dλM=∫λΦ(λ)M(λ)dλS=∫λΦ(λ)S(λ)dλ\begin{aligned} L &= \int_{\lambda}\Phi(\lambda)L(\lambda)d\lambda \\ M &= \int_{\lambda}\Phi(\lambda)M(\lambda)d\lambda \\ S &= \int_{\lambda}\Phi(\lambda)S(\lambda)d\lambda \end{aligned}

LL、MM、SS 称为视锥细胞响应的三刺激值（tristimulus values）。容易知道，类似 LL、MM、SS 这种线性积分形式的颜色表示，向量 (L,M,S)(L,M,S) 的数乘和加法自动保持了颜色的数乘（正比律）和加法（加法律）。

cone-response-function.png

颜色匹配实验

根据三刺激值可知，人眼的视觉系统并不是一个波长探测器，而是一个线性积分器。这导致了同色异谱（metamerism）现象：输入光谱 Φ1(λ)\Phi_{1}(\lambda)、Φ2(λ)\Phi_{2}(\lambda) 不同，但色觉响应 (L,M,S)(L,M,S) 相同。同色异谱是人眼视觉的关键特征，它让颜色复现成为可能，它也是颜色匹配实验的基础。

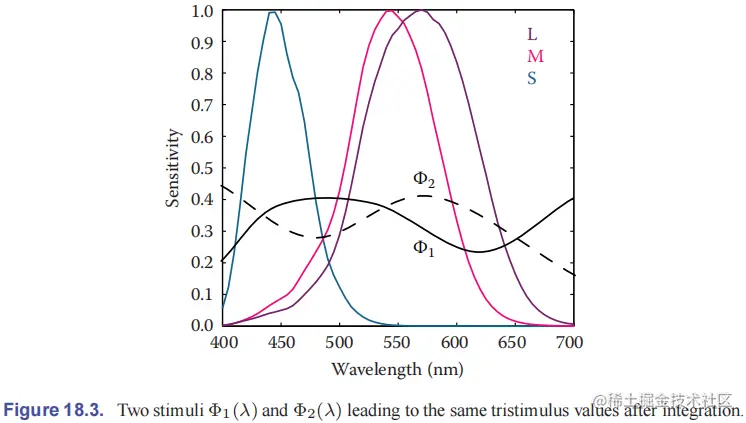
metamerism.png

假定选择三个不同的颜色作为原色（primary）。通过调节它们的强度，使得加法混合（格拉斯曼定律）后的三刺激值和第四种颜色相同（同色异谱），此时称为颜色匹配（color match），而混合系数可作为第四种颜色的表示。

标准观测者（Standard Observers）

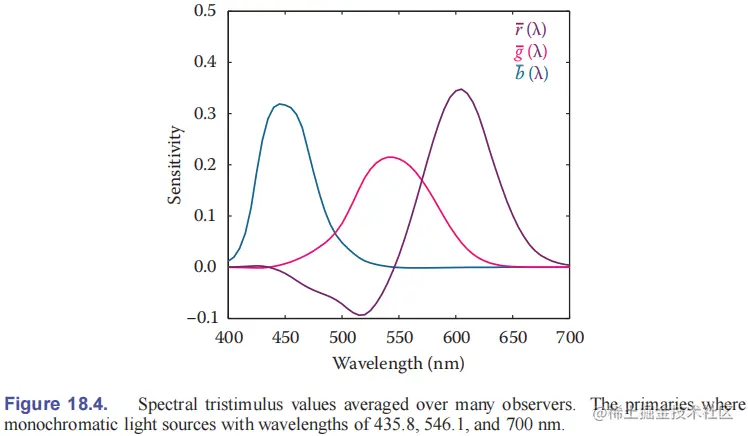
为了更加方便地进行颜色匹配，需要知道视锥细胞响应谱，并对不同的观测者平均以消除偏差。国际照明委员会（Commission Internationale de l´Eclairage，简称 CIE）规定波长 435.8 nm435.8\ \text{nm}、546.1 nm546.1\ \text{nm}、700 nm700\ \text{nm} 的单色光为三原色。对可见光波段进行颜色匹配，并对观测者平均，可以得到波长为 λ\lambda 的单色光在三原色下的表示，即颜色匹配函数（color matching function）rˉ(λ)\bar{r}(\lambda)、gˉ(λ)\bar{g}(\lambda)、bˉ(λ)\bar{b}(\lambda)。任意光谱 Φ(λ)\Phi(\lambda) 的三刺激值分别为：

R=∫λΦ(λ)rˉ(λ)dλG=∫λΦ(λ)gˉ(λ)dλB=∫λΦ(λ)bˉ(λ)dλ\begin{aligned} R &= \int_{\lambda}\Phi(\lambda)\bar{r}(\lambda)d\lambda \\ G &= \int_{\lambda}\Phi(\lambda)\bar{g}(\lambda)d\lambda \\ B &= \int_{\lambda}\Phi(\lambda)\bar{b}(\lambda)d\lambda \end{aligned}

颜色匹配函数也可以看作是单色光的三刺激值。根据格拉斯曼定律容易知道：

Φ(λ)=∫λ′Φ(λ′)δλ′(λ)dλ′∼∫λ′Φ(λ′)[rˉ(λ′)δλR(λ)+gˉ(λ′)δλG(λ)+bˉ(λ′)δλB(λ)]dλ′=RδλR(λ)+GδλG(λ)+BδλB(λ)\begin{aligned} \Phi(\lambda) &= \int_{\lambda'}\Phi(\lambda')\delta_{\lambda'}(\lambda)d\lambda' \\ &\sim \int_{\lambda'}\Phi(\lambda')[\bar{r}(\lambda')\delta_{\lambda_{R}}(\lambda) + \bar{g}(\lambda')\delta_{\lambda_{G}}(\lambda) + \bar{b}(\lambda')\delta_{\lambda_{B}}(\lambda)]d\lambda' \\ &= R\delta_{\lambda_{R}}(\lambda) + G\delta_{\lambda_{G}}(\lambda) + B\delta_{\lambda_{B}}(\lambda) \end{aligned}

这里采用了形式 δλ′(λ)≡δ(λ−λ′)\delta_{\lambda'}(\lambda)\equiv\delta(\lambda - \lambda') 表示狄拉克函数。

即，按 RR、GG、BB 对三原色混合后的光与光谱 Φ(λ)\Phi(\lambda) 匹配，这说明若三刺激值 RR、GG、BB 相同，则颜色一定匹配。计算三原色混合后光谱的 LL、MM、SS 值：

[LMS]=∫λdλ(RδλR(λ)+GδλG(λ)+BδλB(λ))[L(λ)M(λ)S(λ)]=[L(λR)L(λG)L(λB)M(λR)M(λG)M(λB)S(λR)S(λG)S(λB)][RGB]\begin{aligned} \begin{bmatrix} L \\ M \\ S \end{bmatrix} &= \int_{\lambda}d\lambda\left(R\delta_{\lambda_{R}}(\lambda) + G\delta_{\lambda_{G}}(\lambda) + B\delta_{\lambda_{B}}(\lambda)\right) \begin{bmatrix} L(\lambda) \\ M(\lambda) \\ S(\lambda) \end{bmatrix} \\ &= \begin{bmatrix} L(\lambda_{R}) & L(\lambda_{G}) & L(\lambda_{B}) \\ M(\lambda_{R}) & M(\lambda_{G}) & M(\lambda_{B}) \\ S(\lambda_{R}) & S(\lambda_{G}) & S(\lambda_{B}) \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix} \end{aligned}

可以知道，任意光谱的 LL、MM、SS 与 RR、GG、BB 之间由矩阵变换联系起来，这说明互相匹配的颜色的 RR、GG、BB 值相同。因此，RR、GG、BB 构成了颜色的一种表示，可以直接通过这一表示来比较颜色。

负值表示为待匹配颜色加上一个等值的颜色。

color-matching-function.png

由于

  1. 20 世纪 30 年代数值积分难以进行，尤其对有正有负的函数；
  2. CIE 已经发展了视锥细胞光亮度响应函数（photopic luminance response function）V(λ)V(\lambda)；

因此，CIE 给了一组正的颜色匹配函数 xˉ(λ)\bar{x}(\lambda)、yˉ(λ)\bar{y}(\lambda)、zˉ(λ)\bar{z}(\lambda)，称为 CIE 1931 标准观测者，其中 yˉ(λ)=V(λ)\bar{y}(\lambda)=V(\lambda)。相应的三刺激值记为 XX、YY、ZZ，它和 RR、GG、BB 之间满足如下变换：

[XYZ]=10.17697[0.49000.31000.20000.176970.812400.010630.00000.01000.9900][RGB]\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} = \frac{1}{0.17697} \begin{bmatrix} 0.4900 & 0.3100 & 0.2000 \\ 0.17697 & 0.81240 & 0.01063 \\ 0.0000 & 0.0100 & 0.9900 \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix}

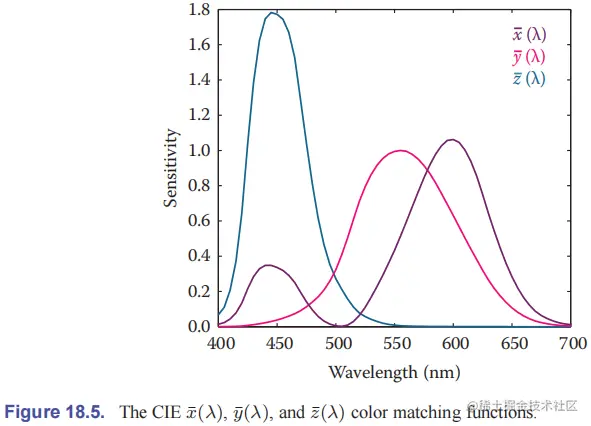
CIE-1931.png

为了保证颜色匹配函数全为正，必须允许虚原色（imaginary primaries），即物理上无法实现的颜色，而是直接用相应的颜色匹配函数来表示。

实际上，类似的任意线性积分形式的颜色表示，和 RR、GG、BB 之间都可以由一个矩阵变换联系起来，由于颜色匹配函数就是单色光的三刺激值，因此这个矩阵变换也是颜色匹配函数之间的变换。

色坐标（Chromaticity Coordinates）

以三刺激值 XX、YY、ZZ 为轴构成的、用于表示颜色的三维空间称为色空间（color space）。真实颜色所占据的区域称为色域（color gamut）。由于 yˉ(λ)\bar{y}(\lambda) 是光亮度响应函数，因此 YY 就是颜色的亮度（luminance）。这使得三刺激值可以投影到二维空间，近似表示与亮度无关的色度信息（chromatic information）。这一投影称为色度图（chromaticity diagram），可以通过归一化并移除亮度信息来得到：

x=XX+Y+Zy=YX+Y+Zz=ZX+Y+Z\begin{aligned} x &= \frac{X}{X + Y + Z} \\ y &= \frac{Y}{X + Y + Z} \\ z &= \frac{Z}{X + Y + Z} \end{aligned}

通常省略 zz 值，以 xx、yy 坐标画出色度。使用这两个色度坐标和一个三刺激值，通常是 YY，可以找到另外两个三刺激值：

X=xyYZ=1−x−yyY\begin{aligned} X &= \frac{x}{y}Y \\ Z &= \frac{1 - x - y}{y}Y \end{aligned}

单色光在色度图上形成的曲线称为光谱轨迹（spectrum loci）。将光谱 Φ1\Phi_{1}、Φ2\Phi_{2} 按 k1k_{1}、k2k_{2} 比例系数混合起来得到光谱 Φ3=k1Φ1+k2Φ2\Phi_{3}=k_{1}\Phi_{1}+k_{2}\Phi_{2}，容易计算它的色坐标一定在 Φ1\Phi_{1}、Φ2\Phi_{2} 的连线上：

[x3y3]=1k1T1+k2T2(k1[X1Y1]+k2[X2Y2])=1k1T1+k2T2(k1T1[x1y1]+k2T2[x2y2])\begin{aligned} \begin{bmatrix} x_{3} \\ y_{3} \end{bmatrix} &= \frac{1}{k_{1}T_{1} + k_{2}T_{2}} \left(k_{1} \begin{bmatrix} X_{1} \\ Y_{1} \end{bmatrix} + k_{2} \begin{bmatrix} X_{2} \\ Y_{2} \end{bmatrix} \right) \\ &= \frac{1}{k_{1}T_{1} + k_{2}T_{2}} \left(k_{1}T_{1} \begin{bmatrix} x_{1} \\ y_{1} \end{bmatrix} + k_{2}T_{2} \begin{bmatrix} x_{2} \\ y_{2} \end{bmatrix} \right) \end{aligned}

其中，Ti=Xi+Yi+ZiT_{i}=X_{i}+Y_{i}+Z_{i}。由此可知，一组光源的色坐标凸包就是这组光源能够表示的所有色度。由于任何光谱都可以分解为单色光的叠加，因此，其它所有光谱都会落在光谱轨迹凸包内。

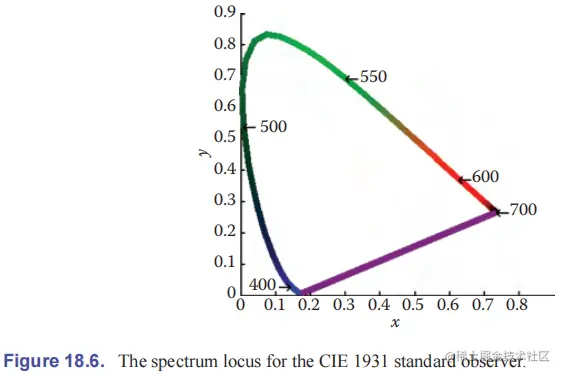
spectrum-locus.png

上图中紫色的线是短波和长波的混合，而非单色光。找出所有原色光在色度图上的坐标，这些色坐标的凸包就是这组原色光通过加法混合所能够表示出的颜色范围。

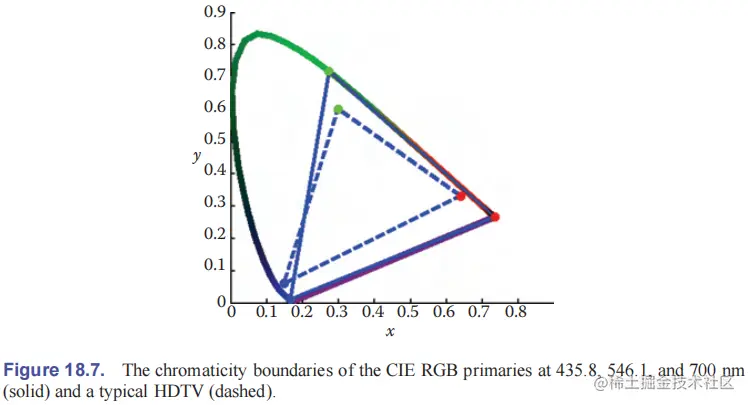
chromaticity-boundary.png

虽然色度图可以很好地洞察加色混合，但仍有两个问题：

  1. 任何颜色复现系统都有自己的原色，而且只能复现色度图中的一部分；
  2. 由于 CIE 颜色匹配函数并不等同于人眼的视锥细胞响应，因此色度图中两点间距不能很好地衡量颜色感知上的差别；

更常用的是 CIE u′v′u'v' 色度图，它在视觉上更加均匀，可以从 XX、YY、ZZ 中计算出来：

u′=4XX+15Y+3Zv′=9YX+15Y+3Z\begin{aligned} u' &= \frac{4X}{X + 15Y + 3Z} \\ v' &= \frac{9Y}{X + 15Y + 3Z} \end{aligned}

也可以由色坐标 (x,y)(x,y) 计算：

u′=4x−2x+12y+3v′=9y−2x+12y+3\begin{aligned} u' &= \frac{4x}{-2x + 12y + 3} \\ v' &= \frac{9y}{-2x + 12y + 3} \end{aligned}

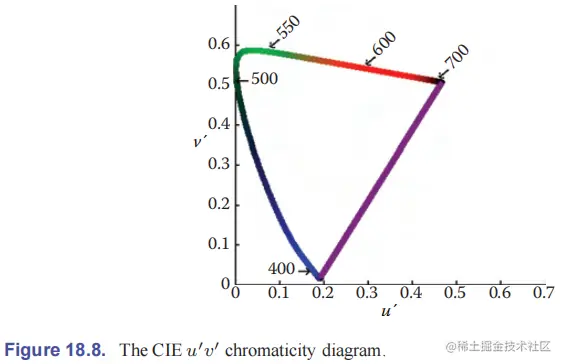
CIEuv.png

色空间

由于 (X,Y,Z)(X,Y,Z) 对应的是虚原色，而且 XYZ 空间中大量的点都没有物理上的真实颜色与之对应，这使得存储效率很低，因而需要更高的位深（bit-depth）来保证图像在视觉上完整性。虽然有可能制造一个接近于 CIE XYZ 颜色匹配函数的设备，但是硬件和图像处理方面所需付出的代价使这种做法没有吸引力。出于这些原因，有必要设计其它的物理可实现（physical realizability）、编码高效（efficient encoding）、感知均匀（perceptual uniformity）、颜色描述直观（intuitive color specification）的色空间。

CIE XYZ 色空间常用于其他色空间之间的转换，它可以看作是设备无关的色空间（device-independent color space）。线性可加三色显示器（linear and additive trichromatic display devices）可以从 CIE XYZ 经一个 3×33\times 3 矩阵变换而来。非线性变换有时也需要，比如，当数据用有限位深存储时，最小化感知误差（perceptual errors），或是直接展示在非线性设备上——输入信号与输出光信号之间存在非线性关系。

构造矩阵变换

对于那些基于红、绿、蓝三原色的显示设备，通过测量输入颜色向量为 (1,0,0)(1,0,0)、(0,1,0)(0,1,0)、(0,0,1)(0,0,1) 时所发出的光谱，可以计算出相应的色坐标 (xR,yR)(x_{R},y_{R})、(xG,yG)(x_{G},y_{G})、(xB,yB)(x_{B},y_{B})。颜色向量为 (1,1,1)(1,1,1) 时设备输出的光谱称为白点（white point），相应的色坐标为 (xW,yW)(x_{W},y_{W})。三原色和白点刻画了整个显示设备，并且决定了显示器色空间和 CIE XYZ 之间的变换矩阵。

如果知道了白点最大亮度，可以计算相应的三刺激值 (XW,YW,ZW)(X_{W},Y_{W},Z_{W})，并通过求解下面的线性方程组得到亮度比 SRS_{R}、SGS_{G}、SBS_{B}：

XW=xRSR+xGSG+xBSBYW=yRSR+yGSG+yBSBZW=zRSR+zGSG+zBSB\begin{aligned} X_{W} &= x_{R}S_{R} + x_{G}S_{G} + x_{B}S_{B} \\ Y_{W} &= y_{R}S_{R} + y_{G}S_{G} + y_{B}S_{B} \\ Z_{W} &= z_{R}S_{R} + z_{G}S_{G} + z_{B}S_{B} \end{aligned}

进而得到 XX、YY、ZZ 与设备 RR、GG、BB 之间的变换：

[XYZ]=[xRSRxGSGxBSByRSRyGSGyBSBzRSRzGSGzBSB][RGB]\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} = \begin{bmatrix} x_{R}S_{R} & x_{G}S_{G} & x_{B}S_{B} \\ y_{R}S_{R} & y_{G}S_{G} & y_{B}S_{B} \\ z_{R}S_{R} & z_{G}S_{G} & z_{B}S_{B} \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix}

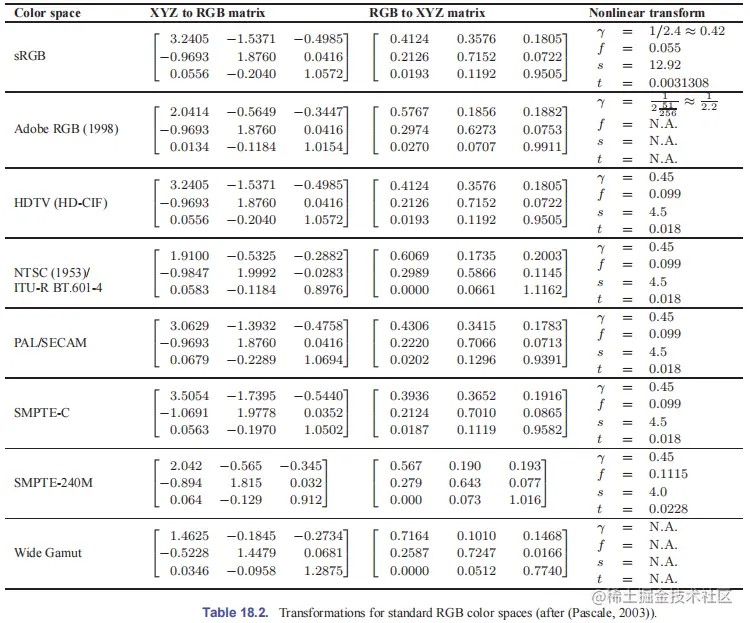
如果未指定设备 RGB 色空间，则一般默认采用标准 RGB 色空间，用于 HDTV 编码和广播的 ITU-R BT.709 标准是一个合理的选择。

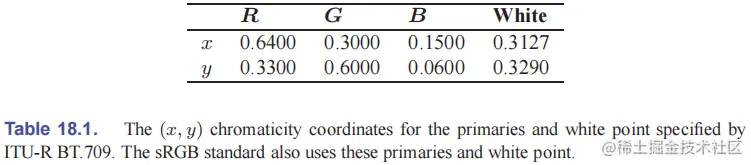
ITU-R_BT.709.png

这个 RGB 色空间与 CIE XYZ 之间的变换如下：

[XYZ]=[0.41240.35760.18050.21260.71520.07220.01930.11920.9505][RGB][RGB]=[3.2405−1.5371−0.4985−0.96931.87060.04160.0556−0.20401.0572][XYZ]\begin{aligned} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} &= \begin{bmatrix} 0.4124 & 0.3576 & 0.1805 \\ 0.2126 & 0.7152 & 0.0722 \\ 0.0193 & 0.1192 & 0.9505 \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix} \\ \begin{bmatrix} R \\ G \\ B \end{bmatrix} &= \begin{bmatrix} 3.2405 & -1.5371 & -0.4985 \\ -0.9693 & 1.8706 & 0.0416 \\ 0.0556 & -0.2040 & 1.0572 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \end{aligned}

sRGB 色空间还多了一个非线性变换，以最小化数字应用的量化误差所导致的感知误差：

RsRGB={1.055 R1/2.4−0.055R>0.0031308,12.92 RR⩽0.0031308;GsRGB={1.055 G1/2.4−0.055G>0.0031308,12.92 GG⩽0.0031308;BsRGB={1.055 B1/2.4−0.055B>0.0031308,12.92 BB⩽0.0031308;\begin{aligned} R_{\text{sRGB}} &= \left\{ \begin{aligned} &1.055\ R^{1/2.4} - 0.055 && R > 0.0031308, \\ &12.92\ R && R \leqslant 0.0031308; \end{aligned} \right. \\ G_{\text{sRGB}} &= \left\{ \begin{aligned} &1.055\ G^{1/2.4} - 0.055 && G > 0.0031308, \\ &12.92\ G && G \leqslant 0.0031308; \end{aligned} \right. \\ B_{\text{sRGB}} &= \left\{ \begin{aligned} &1.055\ B^{1/2.4} - 0.055 && B > 0.0031308, \\ &12.92\ B && B \leqslant 0.0031308; \end{aligned} \right. \end{aligned}

设备依赖的 RGB 空间

每个设备都有自己的原色和白点，因此相应的 RGB 色空间是设备依赖的。由于缺少了颜色管理，同样的一幅 RGB 图像在不同设备上的表现也就不同。通常可以指定图像表示在某个已知的 RGB 色空间，然后转换到设备无关的 XYZ 色空间，再变换到设备自身的 RGB 色空间。有一些 RGB 色空间是定义良好的，它们均由线性变换和非线性变换复合而成，其中，非线性变换形式如下：

Rnonlinear={(1+f)Rγ−ft<R⩽1,sR0⩽R⩽t;Gnonlinear={(1+f)Gγ−ft<G⩽1,sG0⩽G⩽t;Bnonlinear={(1+f)Bγ−ft<B⩽1,sB0⩽B⩽t;\begin{aligned} R_{\text{nonlinear}} &= \left\{ \begin{aligned} &(1 + f)R^{\gamma} - f && t < R \leqslant 1, \\ &sR && 0 \leqslant R \leqslant t; \end{aligned} \right. \\ G_{\text{nonlinear}} &= \left\{ \begin{aligned} &(1 + f)G^{\gamma} - f && t < G \leqslant 1, \\ &sG && 0 \leqslant G \leqslant t; \end{aligned} \right. \\ B_{\text{nonlinear}} &= \left\{ \begin{aligned} &(1 + f)B^{\gamma} - f && t < B \leqslant 1, \\ &sB && 0 \leqslant B \leqslant t; \end{aligned} \right. \end{aligned}

ss、ff、tt、γ\gamma 和原色、白点一起指定了一类 RGB 色空间。

standard-color-space.png

LMS 视锥空间（Cone Space）

视锥细胞响应信号 LMS 与 CIE XYZ 之间的变换称为 Hunt-Pointer-Estevez 变换，可用于色适应变换（chromatic adaptation transforms）和色貌模型（color appearance modeling）。

[LMS]=[0.389710.68898−0.07868−0.229811.183400.046410.000000.000001.00000][XYZ][XYZ]=[1.91019−1.112140.201950.370950.629050.000000.000000.000001.00000][LMS]\begin{aligned} \begin{bmatrix} L \\ M \\ S \end{bmatrix} &= \begin{bmatrix} 0.38971 & 0.68898 & -0.07868 \\ -0.22981 & 1.18340 & 0.04641 \\ 0.00000 & 0.00000 & 1.00000 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \\ \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} &= \begin{bmatrix} 1.91019 & -1.11214 & 0.20195 \\ 0.37095 & 0.62905 & 0.00000 \\ 0.00000 & 0.00000 & 1.00000 \end{bmatrix} \begin{bmatrix} L \\ M \\ S \end{bmatrix} \end{aligned}

CIE 1976 L∗a∗b∗L^{*}a^{*}b^{*}

对立色空间（color opponent space）包含一个无色通道（achromatic channel）——也就是亮度，和两个对立色通道（color opponency channel）——通常是红绿和黄蓝通道。对立色通道在正负轴上分别编码两种颜色，零值表示中性（neutral）。与图形学最相关的对立色系统是 CIE 1976 L∗a∗b∗L^{*}a^{*}b^{*} 颜色模型，也称为 CIELAB，它是一个感知上或多或少均匀的色空间，对色差（color difference）计算很有用。

CIELAB 的输入是三刺激值 (X,Y,Z)(X,Y,Z)，以及在一个已知光源照射下的白色漫反射表面的三刺激值 (Xn,Yn,Zn)(X_{n},Y_{n},Z_{n})。CIELAB 的三通道分别记为 L∗L^{*}、a∗a^{*}、b∗b^{*}，L∗L^{*} 是颜色亮度通道，a∗a^{*}、b∗b^{*} 是对立色通道。它和 XYZ 之间满足如下变换：

[L∗a∗b∗]=[01160−16500−500000200−2000][f(X/Xn)f(Y/Yn)f(Z/Zn)1]f(r)={r3for r>0.0088567.787r+16116for r⩽0.008856\begin{bmatrix} L^{*} \\ a^{*} \\ b^{*} \end{bmatrix} = \begin{bmatrix} 0 & 116 & 0 & −16 \\ 500 & -500 & 0 & 0 \\ 0 & 200 & -200 & 0 \end{bmatrix} \begin{bmatrix} f(X/X_{n}) \\ f(Y/Y_{n}) \\ f(Z/Z_{n}) \\ 1 \end{bmatrix} \\ f(r) = \left\{ \begin{aligned} &\sqrt[3]{r} && \text{for}\ r > 0.008856 \\ &7.787r + \frac{16}{116} && \text{for}\ r \leqslant 0.008856 \end{aligned} \right.

亮度 L∗L^{*} 被归一化到 00（黑）到 100100（白）之间，a∗a^{*}、b∗b^{*} 通常在 [−128,128][-128,128] 上。由于 CIELAB 在感知上近似线性，因此可以直接只用欧氏距离来计算感知色差：

ΔEab∗=[(ΔL∗)2+(Δa∗)2+(Δb∗)2]1/2\Delta E^{*}_{ab} = \left[(\Delta L^{*})^{2} + (\Delta a^{*})^{2} + (\Delta b^{*})^{2}\right]^{1/2}

CIELAB 与 XYZ 之间的逆变换如下：

X=Xn{(L∗116+a∗500+16116)3if L∗+29125a∗>7.999617.787(L∗116+a∗500)if L∗+29125a∗⩽7.9996Y=Yn{(L∗116+16116)3if L∗>7.999617.787L∗116if L∗⩽7.9996Z=Zn{(L∗116−b∗200+16116)3if L∗+2950b∗>7.999617.787(L∗116−b∗200)if L∗+2950b∗⩽7.9996\begin{aligned} X &= X_{n}\left\{ \begin{aligned} &\left(\frac{L^{*}}{116} + \frac{a^{*}}{500} + \frac{16}{116}\right)^{3} && \text{if}\ L^{*} + \frac{29}{125}a^{*} > 7.9996 \\ &\frac{1}{7.787}\left(\frac{L^{*}}{116} + \frac{a^{*}}{500}\right) && \text{if}\ L^{*} + \frac{29}{125}a^{*} \leqslant 7.9996 \end{aligned} \right. \\ Y &= Y_{n}\left\{ \begin{aligned} &\left(\frac{L^{*}}{116} + \frac{16}{116}\right)^{3} && \text{if}\ L^{*} > 7.9996 \\ &\frac{1}{7.787}\frac{L^{*}}{116} && \text{if}\ L^{*} \leqslant 7.9996 \end{aligned} \right. \\ Z &= Z_{n}\left\{ \begin{aligned} &\left(\frac{L^{*}}{116} - \frac{b^{*}}{200} + \frac{16}{116}\right)^{3} && \text{if}\ L^{*} + \frac{29}{50}b^{*} > 7.9996 \\ &\frac{1}{7.787}\left(\frac{L^{*}}{116} - \frac{b^{*}}{200}\right) && \text{if}\ L^{*} + \frac{29}{50}b^{*} \leqslant 7.9996 \end{aligned} \right. \end{aligned}

色适应（Chromatic Adaptation）

CIELAB 中的 (Xn,Yn,Zn)(X_{n},Y_{n},Z_{n}) 已经计入了观测环境。观测物体和图像时所处的环境会在很大程度上影响视觉感知。光照条件包括光的亮度和颜色。

人眼视觉系统对环境变化的响应过程称为适应（adaptation）。适应分三类：明适应（light adaptation，也称光适应）、暗适应（dark adaptation）、色适应（chromatic adaptation）。从非常暗的环境到非常亮的环境时会产生明适应，反之，则产生暗适应。暗适应所需时间通常比明适应的更长。

色适应是指适应——通常是忽略——光照颜色变化的能力。人眼视觉系统可以将观测环境归一化以呈现一致的视觉体验，这在一定程度上保证颜色恒定（color constancy）：尽管光照变化，物体反射率看起来几乎不变。人眼虽然不能完全忽略掉观测环境，但可以明确知道光照条件影响整体色貌，而不是改变物体本身的物理性质。

色适应的计算模型主要关注于视锥细胞的增益控制机制。最简单的模型是，假定每种视锥细胞相互独立地适应所吸收的能量：

La=αLMa=βMSa=γS\begin{aligned} L_{a} &= \alpha L \\ M_{a} &= \beta M \\ S_{a} &= \gamma S \end{aligned}

其中，(La,Ma,Sa)(L_{a},M_{a}, S_{a}) 是色适应视锥信号，α\alpha、β\beta、γ\gamma 是由观测环境决定的相互独立的增益控制，上述色适应称为 von Kries 适应（von Kries adaptation）。

自适应光照（adapting illumination）可以测量场景中的白色表面得到；数字图像中，自适应光照可以近似为场景中的最大三刺激值；这种方式得到的光称为自适应白光（adapting white）(Lw,Ww,Sw)(L_{w},W_{w},S_{w})。von Kries 适应在视锥响应空间中表述为：

[LaMaSa]=[1/Lw0001/Mw0001/Sw][LMS]\begin{bmatrix} L_{a} \\ M_{a} \\ S_{a} \end{bmatrix} = \begin{bmatrix} 1/L_{w} & 0 & 0 \\ 0 & 1/M_{w} & 0 \\ 0 & 0 & 1/S_{w} \end{bmatrix} \begin{bmatrix} L \\ M \\ S \end{bmatrix}

当环境光照切换时，自适应光照从 (Lw,1,Mw,1,Sw,1)(L_{w,1},M_{w,1},S_{w,1}) 变为 (Lw,2,Mw,2,Sw,2)(L_{w,2},M_{w,2},S_{w,2})，物体颜色变为：

[LcMcSc]=[Lw,2000Mw,2000Sw,2][1/Lw,10001/Mw,10001/Sw,1][LMS]\begin{bmatrix} L_{c} \\ M_{c} \\ S_{c} \end{bmatrix} = \begin{bmatrix} L_{w,2} & 0 & 0 \\ 0 & M_{w,2} & 0 \\ 0 & 0 & S_{w,2} \end{bmatrix} \begin{bmatrix} 1/L_{w,1} & 0 & 0 \\ 0 & 1/M_{w,1} & 0 \\ 0 & 0 & 1/S_{w,1} \end{bmatrix} \begin{bmatrix} L \\ M \\ S \end{bmatrix}

虽然存在更复杂、更精确的色适应变换，但是 von Kries 模型仍然非常有效。对渲染而言，色适应的重要性在于，无需调整场景并重新渲染，只需作为图像后处理，即可修正观测环境的光照。为了减少色适应变换带来的量化误差，渲染的图像应保存为浮点格式。

色貌（Color Appearance）

色度学和色适应仍不足以描述真实颜色。为了对真实物体的颜色感知进行预测，还需要更多的环境信息。色貌模型（color appearance model）同时考虑了刺激本身的测量和观测环境。同样的图像在不同观测环境下存在明显差异，色貌模型可用于预测这些差异以准确地复现颜色。虽然色貌模型在颜色复现方面很重要，但实现起来非常复杂而繁琐。

avatar
文章
阅读
粉丝