CV大模型系列之：扩散模型基石DDPM（人人都能看懂的数学原理篇）

猛猿
7,554 阅读17分钟

⚠️⚠️⚠️本文为稀土掘金技术社区首发签约文章，30天内禁止转载，30天后未获授权禁止转载，侵权必究！

本篇将和大家一起解读扩散模型的基石：DDPM(Denoising Diffusion Probalistic Models) 。扩散模型的研究并不始于DDPM，但DDPM的成功对扩散模型的发展起到至关重要的作用。在这个系列里我们也会看到，后续一连串效果惊艳的模型，都是在DDPM的框架上迭代改进而来。所以，我把DDPM放在这个系列的第一篇进行讲解。

初读DDPM论文的朋友，可能有以下两个痛点：

  • 论文花极大篇幅讲数学推导，可是我看不懂。

  • 论文没有给出模型架构图和详细的训练解说，而这是我最关心的部分。

针对这些痛点，DDPM系列将会出如下三篇文章：

  • DDPM（模型架构篇）：在阅读源码的基础上，本篇绘制了详细的DDPM模型架构图（DDPM UNet） 同时附上关于模型运作流程的详细解说。本篇不涉及数学知识，直观帮助大家了解DDPM怎么用，为什么好用。

  • DDPM（人人都能看懂的数学推理篇）：也就是本篇文章，DDPM的数学推理可能是很多读者头疼的部分。我尝试跳出原始论文的推导顺序和思路，从更符合大家思维模式的角度入手，把整个推理流程串成一条完整的逻辑线。本文涵盖大量图例，更好帮助大家理解抽象公式。

  • DDPM（源码解读篇）：在前两篇的基础上，我们将配合模型架构图，一起阅读DDPM源码，并实操跑一次，观测训练过程里的中间结果。

CV大模型系列文章导航（持续更新中）：
🌸CV大模型系列之：扩散模型基石DDPM（模型架构篇）🌸
🌸CV大模型系列之：扩散模型基石DDPM（人人都能看懂的数学原理篇）🌸
🌸CV大模型系列之：扩散模型基石DDPM（源码解读与实操篇）🌸
🌸CV大模型系列之：全面解读VIT，它到底给植树人挖了多少坑🌸
🌸CV大模型系列之：多模态经典之作CLIP，探索图文结合的奥秘🌸
🌸CV大模型系列之：MAE，实现像素级图像重建🌸
🌸CV大模型系列之：MoCo v1，利用对比学习在CV任务上做无监督训练🌸
🌸CV大模型系列之：DALLE2，OpenAI文生图代表作解读🌸

一、DDPM在做一件什么事

在DDPM模型架构篇中，我们已经讨论过DDPM的作用，以及它为何能成为扩散模型/文生图模型基石的原因。这里为了方便读者更好了解上下文，我们将相关讲解再放一次。

假设你想做一个以文生图的模型，你的目的是给一段文字，再随便给一张图（比如一张噪声），这个模型能帮你产出符合文字描述的逼真图片，例如：

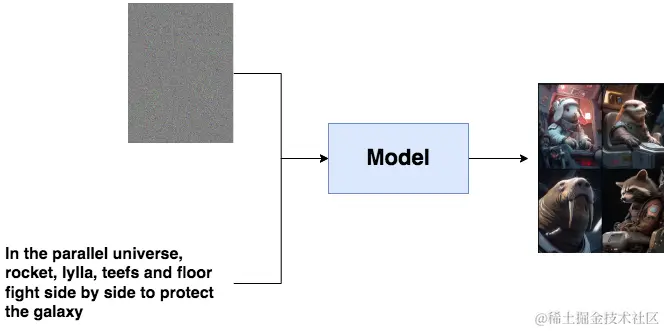
文字描述就像是一个指引(guidance)，帮助模型去产生更符合语义信息的图片。但是，毕竟语义学习是复杂的。我们能不能先退一步，先让模型拥有产生逼真图片的能力？

比如说，你给模型喂一堆cyperpunk风格的图片，让模型学会cyperpunk风格的分布信息，然后喂给模型一个随机噪音，就能让模型产生一张逼真的cyperpunk照片。或者给模型喂一堆人脸图片，让模型产生一张逼真的人脸。同样，我们也能选择给训练好的模型喂带点信息的图片，比如一张夹杂噪音的人脸，让模型帮我们去噪。

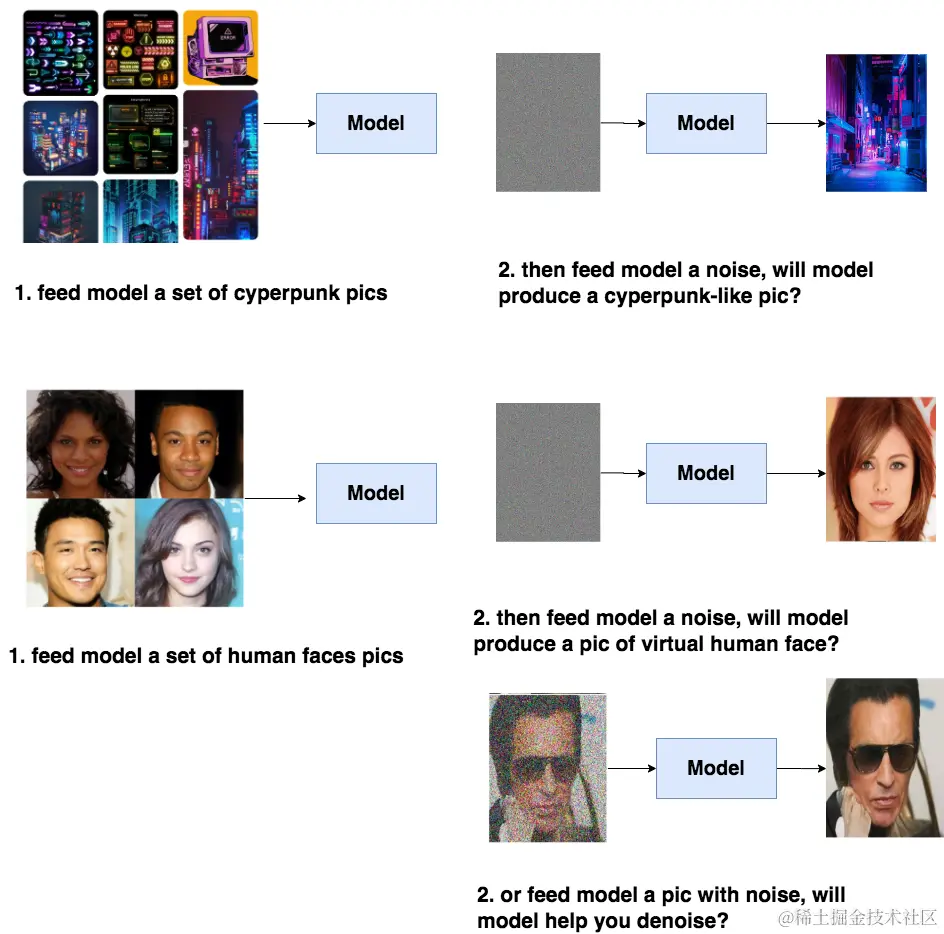
具备了产出逼真图片的能力，模型才可能在下一步中去学习语义信息(guidance)，进一步产生符合人类意图的图片。而DDPM的本质作用，就是学习训练数据的分布，产出尽可能符合训练数据分布的真实图片。所以，它也成为后续文生图类扩散模型框架的基石。

二、优化目标

现在，我们知道DDPM的目标就是：使得生成的图片尽可能符合训练数据分布。基于这个目标，我们记：

  • Pθ(x)P_{\theta}(x)：模型所产生的图片的（概率）分布。其中θ\theta表示模型参数，以θ\theta作为下标的目的是表示这个分布是由模型决定的，
  • Pdata(x)P_{data}(x)：训练数据（也可理解为真实世界）图片的（概率）分布。下标data表示这是一个自然世界客观存在的分布，与模型无关。

则我们的优化目标可以用图例表示为：

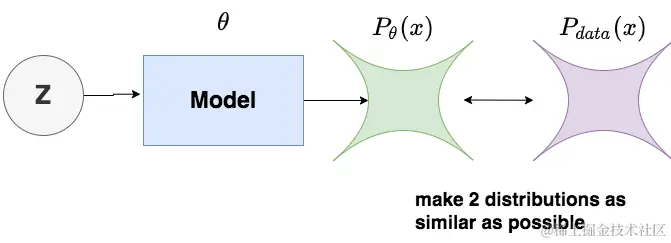
而求两个分布之间的相似性，我们自然而然想到了KL散度 复习一下KL散度的定义：分布p与分布q之间的KL散度为：

DKL(p∣∣q)=∑i=1mp(xi)logp(xi)q(xi)(原始定义)=−∑i=1mp(xi)logq(xi)p(xi)(稍作变式)=−∫xp(x)logq(x)p(x)dx(m→∞)\begin{align} D_{KL}(p||q) &=\sum_{i=1}^{m}p(x_i)log\frac{p(x_i)}{q(x_i)} (原始定义) \notag\\ &= -\sum_{i=1}^{m}p(x_i)log\frac{q(x_i)}{p(x_i)} (稍作变式) \notag\\ &= -\int\limits_{x}p(x)log\frac{q(x)}{p(x)}dx (m\to \infty ) \tag{1.1}\\ \end{align}

则现在我们的目标函数就变为：

argminθKL(Pdata∣∣Pθ){argmin}_\theta KL(P_{data}||P_{\theta})

我们利用利用式（1.1），对该目标函数做一些变换（可向右拖动公式，阅读公式注解）

image.png

经过这一番转换，我们的优化目标从直觉上的“令模型输出的分布逼近真实图片分布”转变为argmaxθ∏i=1mPθ(xi)argmax_{\theta}\prod_{i=1}^{m} P_{\theta}(x_i) ，我们也可以把这个新的目标函数通俗理解成使得模型产生真实图片的概率最大。如果一上来就直接把式（1.2）作为优化目标，可能会令很多朋友感到困惑。因此在这一步中，我们解释了为什么要用式（1.2）作为优化目标。

接下来，我们近一步来看，对式（1.2）还能做什么样的转换和拆解。

三、最大化ELBO（Evidence Lower Bound）

argmaxθ∏i=1mPθ(xi)argmax_{\theta}\prod_{i=1}^{m} P_{\theta}(x_i) 的本质就是要使得连乘中的每一项最大，也等同于使得logPθ(x)logP_{\theta}(x) 最大。所以我们进一步来拆解logPθ(x)logP_{\theta}(x) 。在开始拆解之前，让我们先回顾一下扩散模型的加噪与去噪过程，帮助我们更好地做数学推理。

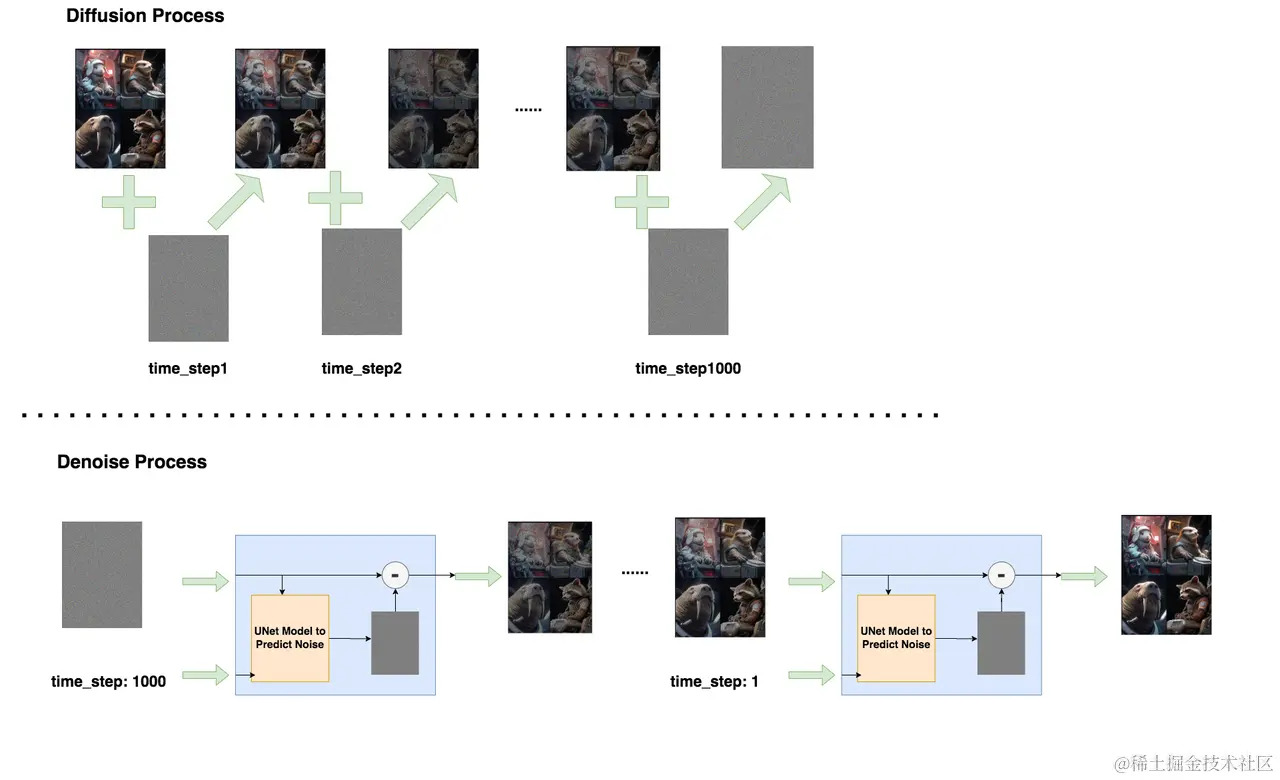
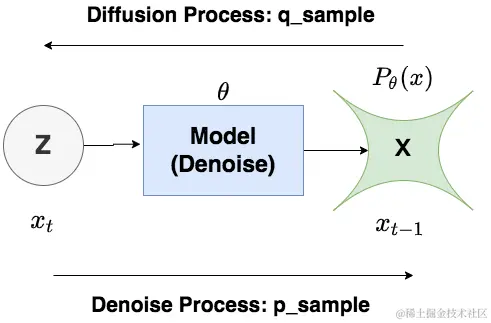
在Diffusion Process中，我们不过模型，而是按照设置好的加噪规则，随着time_step的变化，给图片添加噪声（xt−1 → xtx_{t-1} \to x_{t}）。在Denoise Process中，我们则需要经过模型，对图片进行去噪，逐步将图片还原成原始的样子（xt → xt−1x_{t} \to x_{t-1}）。Diffusion过程中遵循的分布，我们记为qq，Denoise过程中遵循的分布，我们记为pθp_{\theta}。严格来说，Diffusion过程遵循的分布应该记为qϕq_{\phi}，下标ϕ\phi也表示模型参数，也就是说， “规则”也算一种“模型” 。理论上，你想对Diffusion单独训练一套模型，也是没有问题的。为了表述严谨，我们接下来都将用qϕq_{\phi}进行表示。

现在我们可以回到拆解logPθ(x)logP_{\theta}(x) 了，即然x和z与Diffusion和Denoise的过程密切相关，那么我们的目标就是要把logPθ(x)logP_{\theta}(x) 拆解成用qϕ, Pθq_{\phi}, P_{\theta}同时表达的形式：

image.png

Eqϕ(z∣x)[logPθ(x,z)qϕ(z∣x)]E_{q_{\phi}(z|x)}[log\frac{P_{\theta}(x, z)}{q_{\phi}(z|x)}]就被称为Evidence Lower Bound (ELBO)。到这一步为止，我们将最大化logPθ(x)logP_{\theta}(x) 拆解成最大化ELBO，其中qθq_{\theta}与diffusion过程密切相关，PθP_{\theta}与denoise过程密切相关。

(2.1)这个公式一出，大家是不是很眼熟？没错，它其实也刻画了VAE的优化目标，所以这里我们才选用z而不是x来表示latent space中的变量。有些读者可能已经发现了，（2.1）描述的是一个time_step下的优化目标，但是我们的扩散模型，是有T个time_step的，因此，我们还需要把（2.1）再进一步扩展成链式表达的方式。在这一步扩展里，我们将不再使用z变量，取而代之的是用x0, ... xTx_{0}, ... x_{T}来表示，更符合我们对扩散模型的整体理解，则我们有：

到这一步位置，我们只是拆解了一个time_step，即xt → xt−1x_{t} \to x_{t-1}，我们知道扩散模型的过程是包含多个time_step的，因此我们可以根据式（2.1）进一步拆解成链式表达的形式：

logPθ(x)≥Eqϕ(x1:xT∣x0)logPθ(x0:xT)qϕ(x1:xT∣x0)\begin{align} logP_{\theta}(x) &\ge E_{q_{\phi}(x_{1}:x_{T}|x_{0})}log\frac{P_{\theta}(x_{0}:x_{T})}{q_{\phi}(x_{1}:x_{T}|x_{0})} \tag{2.2} \end{align}

其中，x0x_{0}表示从真实世界中筛选出来的干净的图片，xTx_{T}表示最后一个time_step加噪后的图片，通常是一个近似纯噪声。细心的读者可能发现，在（2.2）公式中，左边的logPθ(x)logP_{\theta}(x)是不是写成logPθ(x0)logP_{\theta}(x_{0})更合理呀？没错，因为扩散模型的目标就是去还原来自真实世界的x0x_{0}。但这里为了前后表达统一，就不做修改了。读者们只要理解（2.2）的含义即可。

四、进一步拆解ELBO

复习一下，到这一步为止，我们经历了如下过程：

  • 首先，总体优化目标是让模型产生的图片分布和真实图片分布尽量相似，也就是argminθKL(Pdata∣∣Pθ){argmin}_\theta KL(P_{data}||P_{\theta})

  • 对KL散度做拆解，将优化目标argminθKL(Pdata∣∣Pθ){argmin}_\theta KL(P_{data}||P_{\theta})转变为argmaxθ∏i=1mPθ(xi)argmax_{\theta}\prod_{i=1}^{m} P_{\theta}(x_i) ，同时也等价于让连乘项中的每一项logPθ(x)logP_{\theta}(x) 最大

  • 对logPθ(x)logP_{\theta}(x) 做拆解，以优化DDPM其中一个time_step为例，将优化目标转向最大化下界（ELBO）Eqϕ(z∣x)[logPθ(x,z)qϕ(z∣x)]E_{q_{\phi}(z|x)}[log\frac{P_{\theta}(x, z)}{q_{\phi}(z|x)}]

  • 以全部time_step为例，将优化目标转变为Eqϕ(x1:xT∣x0)logPθ(x0:xT)qϕ(x1:xT∣x0)E_{q_{\phi}(x_{1}:x_{T}|x_{0})}log\frac{P_{\theta}(x_{0}:x_{T})}{q_{\phi}(x_{1}:x_{T}|x_{0})}，也就是式（2.2）

恭喜你充满耐心地看到这一步了！接下来，我们还需要再耐心对式（2.2）进行拆解，毕竟现在它只是一个偏抽象的形式，因此我们还需对p与q再做具象化处理。之前我们提过，qϕq_{\phi}下标的意思是强调从理论上来说，diffusion过程可以通过训练一个模型来加噪，而并非只能通过规则加噪。这两种方法在数学上都是成立的。由于DDPM采用了后者，因此在接下来的过程中，我们将会去掉下标ϕ\phi。

式（2.2）的进一步拆解如下：

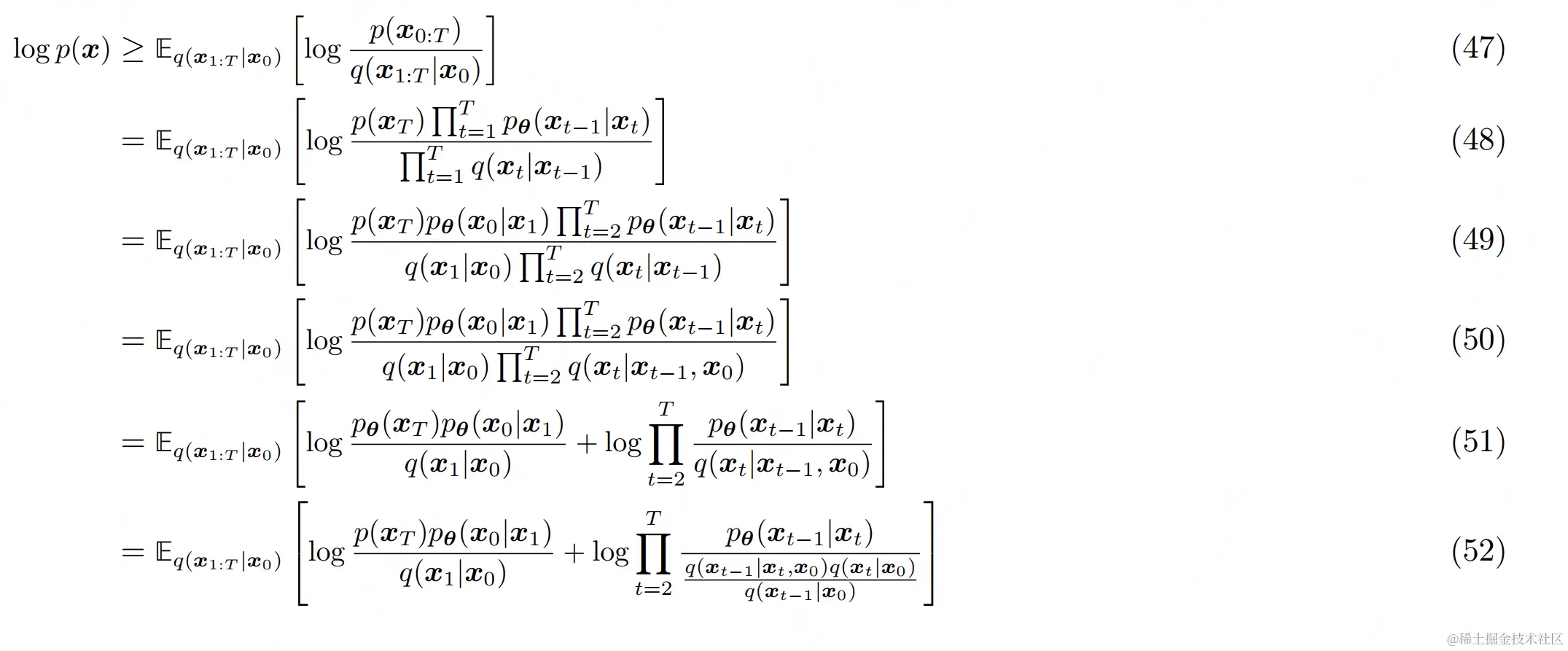
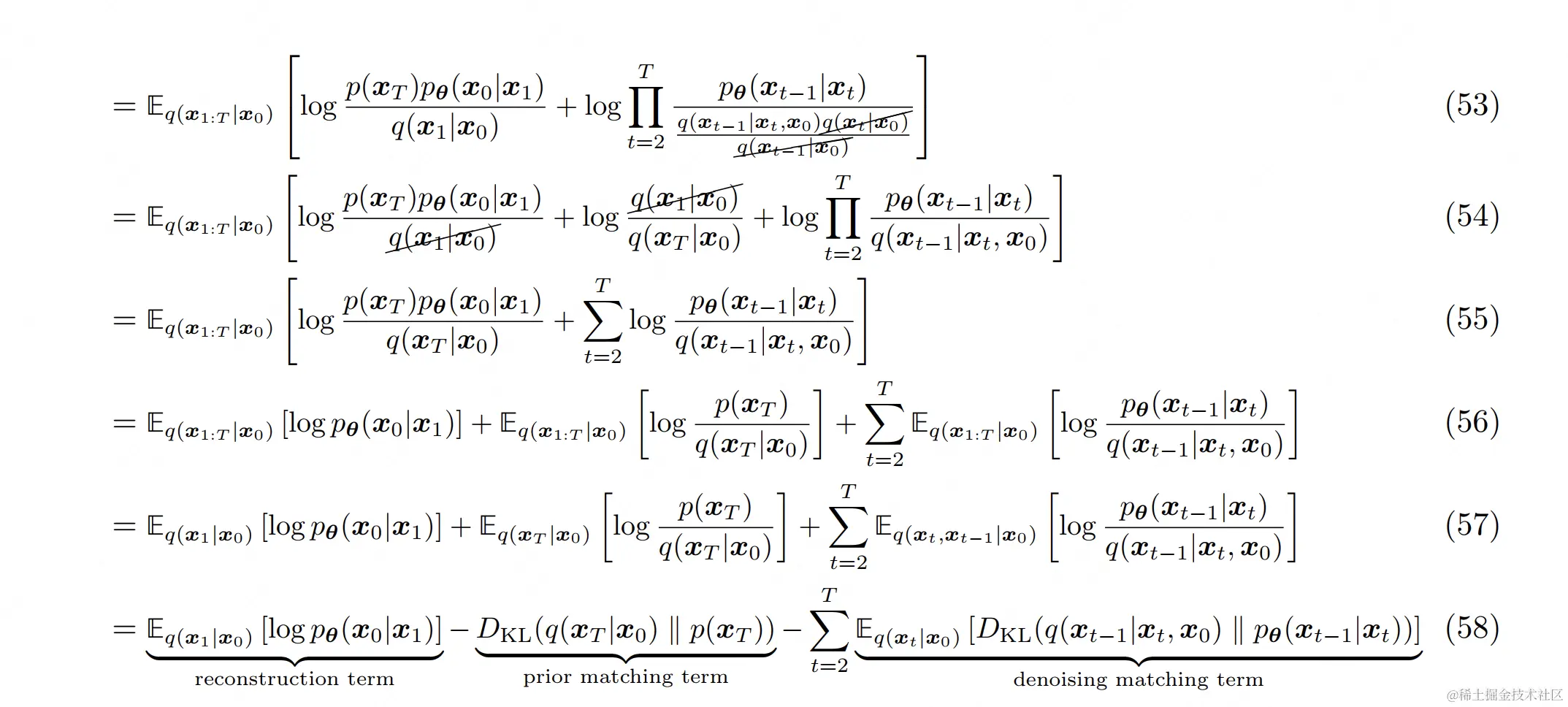
  • （48）：分子上，因为xTx_{T}已是个近似高斯分布的纯噪声，因此它的分布p是已知的，和模型θ\theta无关，所以将p(xT)p(x_{T})单独提炼出。分子与分母的其余项则是因为扩散模型遵循马尔可夫链性质，因此可以通过链式连乘规则进行改写
  • （50)：x0x_{0} 表示来自真实世界的干净图片，它是diffusion过程的起源，任意xtx_{t}都可由x0x_{0} 推导而来，因此可将q(xt∣xt−1)q(x_{t}|x_{t-1}) 改写成q(xt∣xt−1,x0)q(x_{t}|x_{t-1}, x_{0})
  • （52）：根据多变量条件概率的贝叶斯链式法则进行改写，即：
q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)\begin{align} q(x_{t-1}|x_{t}, x_{0}) & = \frac{q(x_{t}|x_{t-1},x_{0})q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})} \notag \end{align}

当然多变量条件概率的改写方式有很多种，根据需要我们选择了上面的这一种

  • （54）：由于q是既定的，可以看作是一个常量，因此可增加logq(x1∣x0)q(xT∣x0)log\frac{q(x_{1} | x_{0})}{q(x_{T}|x_{0})}一项

  • (56)~(57)：根据期望项中涉及到的具体元素，调整期望E的下标

  • （58）：根据KL散度的定义重写最后两项。其中prior matching term可看作是常量，reconstruction term和denoising matching term则是和模型密切相关的两项。由于两者间十分相似，因此接下来我们只需要特别关注denoising matching term如何拆解即可。

五、重参数与噪声预测

现在，我们的优化目标转为最大化∑t=2TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt)]\sum_{t=2}^{T} E_{q(x_{t}|x_{0})}[D_{KL}(q(x_{t-1}|x_{t},x_{0}) || p_{\theta}(x_{t-1}|x_{t})]，我们继续对该项进行拆解。

首先我们来看q(xt−1∣xt,x0)q(x_{t-1}|x_{t},x_{0})一项。

根据多变量条件概率的链式法则，我们有：

q(xt−1∣xt,x0)=q(xt−1,xt,x0)q(xt,x0)=q(xt∣xt−1)q(xt−1∣x0)q(x0)q(xt∣x0)q(x0)=q(xt∣xt−1)q(xt−1∣x0)q(xt∣x0)\begin{align} q(x_{t-1}|x_{t},x_{0}) &= \frac{q(x_{t-1},x_{t},x_{0})}{q(x_{t}, x_{0})} \notag \\ &=\frac{q(x_{t}|x_{t-1})q(x_{t-1}|x_{0})q(x_{0})}{q(x_{t}|x_{0})q(x_{0})} \notag \\ &=\frac{q(x_{t}|x_{t-1})q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})} \notag \end{align}

现在，我们分别来看q(xt∣xt−1)q(x_{t}|x_{t-1})，q(xt−1∣x0)q(x_{t-1}|x_{0})，q(xt∣x0)q(x_{t}|x_{0})具体长什么样子。

5.1 重参数

5.1.1 为什么需要重参数

回顾模型架构篇，我们曾经提过，最朴素的diffusion加噪规则是，在每一个time_step中都sample一次随机噪声，使得：

xt=x0 + ϵ1 + ϵ2 + ... + ϵT \begin{align} x_t = x_{0} + \epsilon_{1} + \epsilon_{2} + ... + \epsilon_{T} \notag \end{align}

在架构篇中，我们直接指出ϵt∼N(0,I)\epsilon_{t} \sim \mathcal{N}(0, I) ，即筛选的噪声是来自一个标准高斯分布。但是为什么要这么设计呢？

我们假设真实世界的图片服从N(μ,σ)\mathcal{N}(\mu, \sigma) 这样的高斯分布，而现在我们的模型PθP_{\theta}就是要去学习这个分布，更具象点，假设模型遵从的分布是N(μθ,σθ)\mathcal{N}(\mu_{\theta}, \sigma_{\theta}) ，我们的目的就是让μθ\mu_{\theta}逼近μ\mu，σθ \sigma_{\theta}逼近σ \sigma。

那么在diffusion过程中，更符合直觉的做法是，模型从N(μθ,σθ)\mathcal{N}(\mu_{\theta}, \sigma_{\theta}) 采样出一个噪声，然后在denoise的过程中去预测这个噪声，这样就能把梯度传递到μθ,σθ\mu_{\theta}, \sigma_{\theta}上，使得模型在预测噪声的过程中习得真实图片的分布。

但这样做产生的问题是，实际上梯度并不能传递到μθ,σθ\mu_{\theta}, \sigma_{\theta}上。举个简单的例子，假设你从N(μθ,σθ)\mathcal{N}(\mu_{\theta}, \sigma_{\theta}) 随机采样出了一个3，你怎么将这个随机的采样结果和μθ,σθ\mu_{\theta}, \sigma_{\theta}联系起来呢？也就是说，在diffusion过程中，如果我们从一个带参数的分布中做数据采样，在denoise过程中，我们无法将梯度传递到这个参数上。

针对这个问题，有一个简单的解决办法：我从一个确定的分布（不带参数）中做数据采样，不就行了吗？比如，我从N(0,I)\mathcal{N}(0, I) 先采样出一个ϵ\epsilon，然后再令最终的采样结果z为：ϵ ∗ σθ + μθ\epsilon * \sigma_{\theta} + \mu_{\theta}。这样我不就能知道z和μθ,σθ\mu_{\theta}, \sigma_{\theta}间的关系了？同时根据高斯分布性质，z也服从N(μθ,σθ)\mathcal{N}(\mu_{\theta}, \sigma_{\theta}) 分布。

以上“从一个带参数的分布中进行采样”转变到“从一个确定的分布中进行采样”，以解决梯度无法传递问题的方法，就被称为 “重参数”（reparamterization）。 关于重参数原理的更多细节，推荐大家阅读这篇文章（spaces.ac.cn/archives/67…

5.1.2 重参数的具体方法

到这一步根据重参数的思想，我们可以把ϵt∼N(μθ,σθ)\epsilon_{t} \sim\mathcal{N}(\mu_{\theta}, \sigma_{\theta}) 转变为ϵt∼N(0,I)\epsilon_{t} \sim\mathcal{N}(0, I) 了。但是现在的diffusion过程还是太繁琐：每一个time_step都要做一次采样，等我后续做denoise过程去预测噪声，传播梯度的时候，参数θ\theta不仅在这个time_step有，在之前的一系列time_steps中都有，这不是给我计算梯度造成困扰了吗？注意到在diffusion过程中，随着time_step的增加，图片中含有的噪声是越来越多的，那我能不能设定一个函数，使得每个time_step的图片都能由原始图片x0x_{0}加噪推导而来，然后使得噪声的比例随着time_step增加而变大？这样我不就只需要一次采样了吗

当然没有问题，DDPM采用的做法是：

（1）首先，设置超参数β1, β2, ... βT{\beta}_{1}, {\beta}_{2}, ... {\beta}_{T}，满足随着t增大，βt{\beta}_{t}逐渐变大。

（2）令：

αt = 1 − βt  αˉt = α1α2...αt \begin{align} \alpha_t = 1 - \beta_{t} \notag \\ \bar \alpha_t = \alpha_1\alpha_2...\alpha_t \notag \end{align}

易推出αˉt\bar\alpha_{t}随着t增大而逐渐变小

（3）则任意时刻的xtx_{t}都可以由x0x_{0}表示出：

xt=αˉtx0+1−αˉtϵ  (ϵ∼ N(0,I)) \begin{align} x_t = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t}\epsilon \qquad (\epsilon \sim \mathcal{N}(0, I)) \notag \end{align}

我们通过图例来更好理解上面的三步骤：

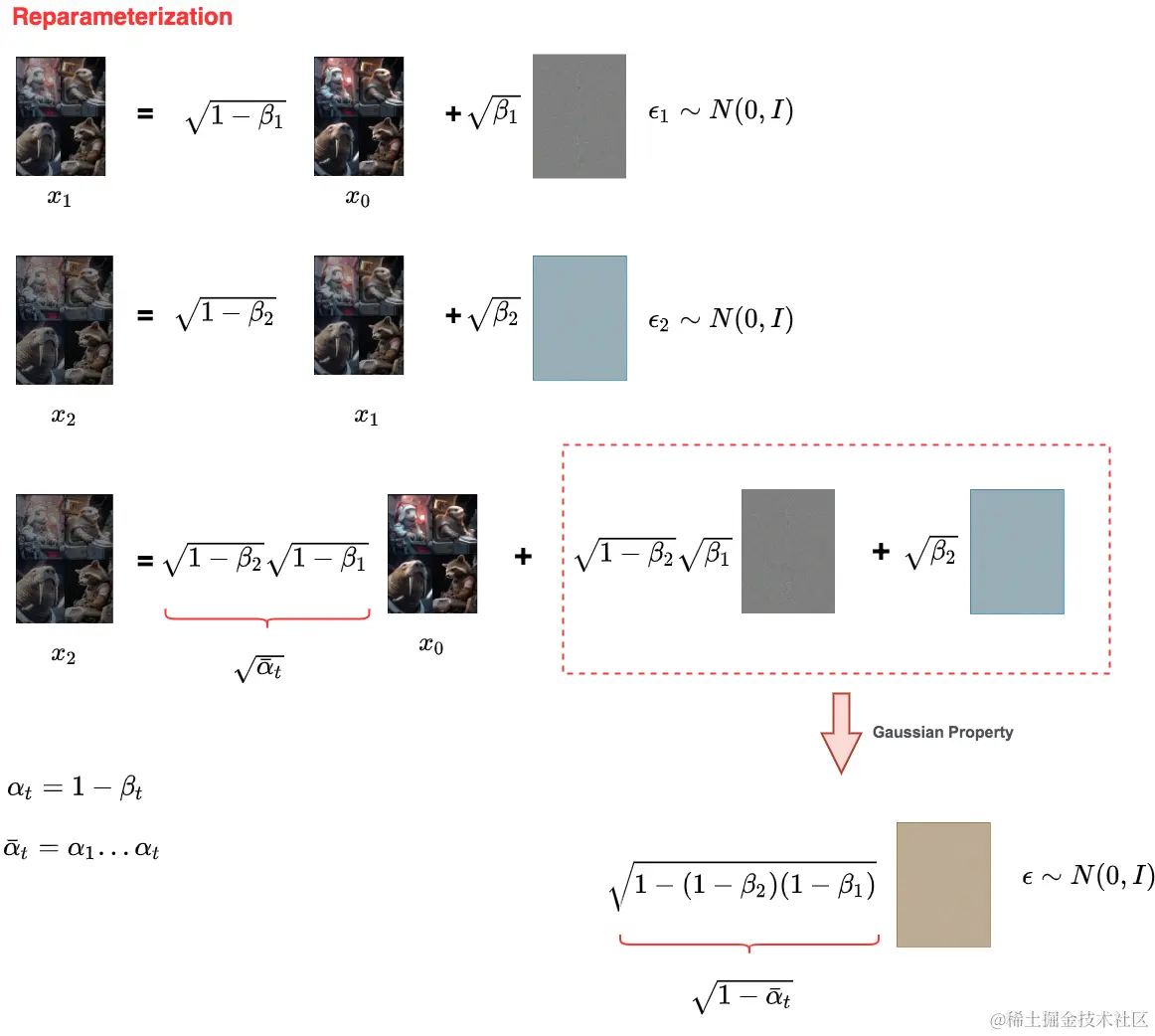
详细的过程都在图例中表示出了，这里不做赘述。

5.2 噪声预测

讲完了重参数的部分，我们继续回到刚才拆解的步骤上来，复习一下，我们已经将ELBO拆解成∑t=2TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt)]\sum_{t=2}^{T} E_{q(x_{t}|x_{0})}[D_{KL}(q(x_{t-1}|x_{t},x_{0}) || p_{\theta}(x_{t-1}|x_{t})]，现在我们的关注点在q分布上，而q分布又由以下三项组成：

q(xt∣xt−1)q(x_{t}|x_{t-1})，q(xt−1∣x0)q(x_{t-1}|x_{0})，q(xt∣x0)q(x_{t}|x_{0})，我们继续来看这三项要怎么具体表示出来

由章节5.1.2，我们知道：

xt=αˉtx0+1−αˉtϵ  (ϵ∼ N(0,I)) \begin{align} x_t = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t}\epsilon \qquad (\epsilon \sim \mathcal{N}(0, I)) \notag \end{align}

则任意x0, xt−1, xtx_{0}, x_{t-1}, x_{t}的关系都可以由此推出：

q(xt∣xt−1):xt=1−βt∗xt−1+βt∗ϵ=αt∗xt−1+1−αt∗ϵq(xt−1∣x0):xt−1=αˉt−1∗x0+1−αˉt−1∗ϵq(xt∣x0):xt=αˉt∗x0+1−αˉt∗ϵ\begin{align} q(x_{t}|x_{t-1}): \quad x_{t} &= \sqrt{1-\beta_{t}}*x_{t-1} + \sqrt{\beta_{t}}*\epsilon \notag \\ &= \sqrt{\alpha_{t}} * x_{t-1} + \sqrt{1-\alpha_{t}} * \epsilon \notag \\ q(x_{t-1}|x_{0}): x_{t-1} &= \sqrt{\bar\alpha_{t-1}}*x_{0} + \sqrt{1-\bar\alpha_{t-1}}*\epsilon \notag\\ q(x_{t}|x_{0}): \quad x_{t} &= \sqrt{\bar\alpha_{t}}*x_{0} + \sqrt{1-\bar\alpha_{t}}*\epsilon \notag\\ \end{align}

友情提示：大家记得看5.1.2中的图例区分αt, αˉt\alpha_{t}, \bar\alpha_{t}哦，不是typo。

同时，我们已经知道（假设）x0, xt−1, xt, ϵx_{0}, x_{t-1}, x_{t}, \epsilon都服从高斯分布，则根据高斯分布的性质，我们有：

q(xt∣xt−1):xt∼N(αtxt−1,(1−αt)I)q(xt−1∣x0):xt−1∼N(αˉt−1x0,(1−αˉt−1)I)q(xt∣x0):xt∼N(αˉtx0,(1−αˉt)I)\begin{align} q(x_{t}|x_{t-1}): \quad &x_{t}\sim N(\sqrt{\alpha_{t}}x_{t-1}, (1-\alpha_{t})I) \notag \\ q(x_{t-1}|x_{0}): \quad &x_{t-1} \sim N(\sqrt{\bar\alpha_{t-1}}x_{0}, (1-\bar\alpha_{t-1})I) \notag\\ q(x_{t}|x_{0}): \quad &x_{t} \sim N(\sqrt{\bar\alpha_{t}}x_{0}, (1-\bar\alpha_{t})I) \notag\\ \end{align}

对于高斯分布，知道了均值和方差，我们就可以把它具体的概率密度函数写出来：

经过这样的一顿爆肝推导，我们终于将q(xt−1∣xt,x0)q(x_{t-1}|x_{t}, x_{0})的分布写出来了（84）。也就是我们当前优化目标∑t=2TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt)]\sum_{t=2}^{T} E_{q(x_{t}|x_{0})}[D_{KL}(q(x_{t-1}|x_{t},x_{0}) || p_{\theta}(x_{t-1}|x_{t})]中的q部分。

现在，我们来看pθ(xt−1∣xt)p_{\theta}(x_{t-1}|x_{t})部分，根据优化目标，此时我们需要让p和q的分布尽量接近：

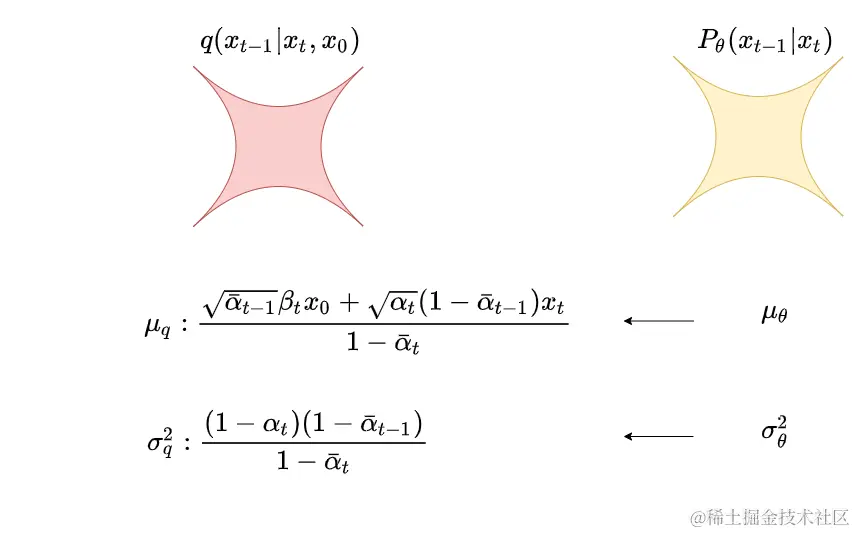image.png 而让p和q的分布接近，等价与让μθ → μq, σθ → σq\mu_{\theta} \to \mu_{q}, \sigma_{\theta} \to \sigma_{q}。注意到σq\sigma_{q}其实是一个常量，它只和超参有关。在DDPM中，为了简化优化过程，并且使训练更稳定，就假设σθ\sigma_{\theta}也按此种方式固定下来了。在后续的扩散模型（例如GLIDE）中，则引入对方差的预测。在DDPM中，只预测均值。

好，那么预测均值，到底是在预测什么东西呢？我们对μq\mu_{q}再做改写，主要是根据我们设置的diffusion规则，将x0x_{0}

用xtx_{t}进行表示：

μq=αˉt−1βtx0+αt(1−αˉt−1)xt1−αˉt=αˉt−1βtxt−1−αˉtϵαˉt+αt(1−αˉt−1)xt1−αˉt=1αt(xt−1−αt1−αˉtϵ)\begin{align} \mu_{q} &= \frac{\sqrt{\bar\alpha_{t-1}}\beta_{t}x_{0} + \sqrt{\alpha_{t}}(1-\bar\alpha_{t-1})x_{t}}{1 - \bar\alpha_{t}} \notag \\ &= \frac{\sqrt{\bar\alpha_{t-1}}\beta_{t}\frac{x_{t} - \sqrt{1-\bar\alpha_{t}}\epsilon}{\sqrt{\bar\alpha_{t}}} + \sqrt{\alpha_{t}}(1-\bar\alpha_{t-1})x_{t}}{1 - \bar\alpha_{t}} \notag \\ &= \frac{1}{\sqrt{\alpha_{t}}}(x_{t} - \frac{1-\alpha_{t}}{\sqrt{1-\bar\alpha_{t}}}\epsilon) \tag{5.1} \end{align}

观察到，式（5.1）的结果在diffusion过程中就已决定好。所以现在对于pθ(xt−1∣xt)p_{\theta}(x_{t-1} | x_{t})，我只要让它在denoise的过程里，预测出ϵθ\epsilon_{\theta}，使得ϵθ→ϵ\epsilon_{\theta}\to\epsilon，然后令：

xt−1=1αt(xt−1−αt1−αˉtϵθ) + σqz (z∼N(0,I)) \begin{align} x_{t-1} &= \frac{1}{\sqrt{\alpha_{t}}}(x_{t} - \frac{1-\alpha_{t}}{\sqrt{1-\bar\alpha_{t}}}\epsilon_{\theta}) + \sigma_{q}z \qquad(z\sim N(0, I)) \notag \end{align}

这样，我不就能使得pθ(xt−1∣xt)p_{\theta}(x_{t-1} | x_{t})和q(xt−1∣xt,x0)q(x_{t-1}|x_{t}, x_{0})的分布一致了吗！

此刻！是不是一道光在你的脑海里闪过！ 一切都串起来了，也就是说，只要在denoise的过程中，让模型去预测噪声，就可以达到让“模型产生图片的分布”和“真实世界的图片分布”逼近的目的！

5.3 再次理解training和sampling

现在，我们再来回顾training和sampling的过程，在training的过程中，我们只需要去预测噪声，就能在数学上使得模型学到的分布和真实的图片分布不断逼近。而当我们使用模型做sampling，即去测试模型能生成什么质量的图片时，我们即可由式(5.1)中的推导结论，从xtx_{t}推导xt−1x_{t-1}，直至还原出x0x_{0}。注意到这里xt−1∼ N(μq, σq)x_{t-1}\sim N(\mu_{q}, \sigma_{q})，其中μq\mu_{q}是我们式（5.1）中要逼近的均值真值；σt = σq\sigma_{t} = \sigma_{q}，则正是我们已经固定住的方差。

关于training和sampling更详细的实操解说，可以参见模型架构篇。

六、总结（必看）

恭喜你坚持看到了这里！我们来把整个推导串成完整的逻辑链：

（1）首先，DDPM总体优化目标是让模型产生的图片分布和真实图片分布尽量相似，也就是argminθKL(Pdata∣∣Pθ){argmin}_\theta KL(P_{data}||P_{\theta})。同时，我们假设真实世界的图片符合高斯分布：Pdata ∼ N(μdata, σdata)P_{data} \sim N(\mu_{data}, \sigma_{data})。因此我们的目标就是要让PθP_{\theta}习得μdata, σdata\mu_{data}, \sigma_{data}

（2）但是μdata, σdata\mu_{data}, \sigma_{data}这两个客观存在的真值是未知的，因此我们必须对KL散度进行不断拆解，直至能用确定的形式将它表示出来。

（3）对KL散度做初步拆解，将优化目标argminθKL(Pdata∣∣Pθ){argmin}_\theta KL(P_{data}||P_{\theta})转变为argmaxθ∏i=1mPθ(xi)argmax_{\theta}\prod_{i=1}^{m} P_{\theta}(x_i) ， 同时也等价于让连乘项中的每一项logPθ(x)logP_{\theta}(x) 最大

（4）继续对logPθ(x)logP_{\theta}(x) 做拆解，以优化DDPM其中一个time_step为例，将优化目标转向最大化下界（ELBO）Eqϕ(z∣x)[logPθ(x,z)qϕ(z∣x)]E_{q_{\phi}(z|x)}[log\frac{P_{\theta}(x, z)}{q_{\phi}(z|x)}]

（5）依照马尔可夫性质，从1个time_step推至所有的time_steps，将（4）中的优化目标改写为Eqϕ(x1:xT∣x0)logPθ(x0:xT)qϕ(x1:xT∣x0)E_{q_{\phi}(x_{1}:x_{T}|x_{0})}log\frac{P_{\theta}(x_{0}:x_{T})}{q_{\phi}(x_{1}:x_{T}|x_{0})}，也就是式（2.2）

（6）对式（2.2）继续做拆解，将优化目标变为∑t=2TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt)]\sum_{t=2}^{T} E_{q(x_{t}|x_{0})}[D_{KL}(q(x_{t-1}|x_{t},x_{0}) || p_{\theta}(x_{t-1}|x_{t})]

（7）先来看（6）中的q(xt−1∣xt,x0)q(x_{t-1}|x_{t}, x_{0})一项，注意到这和diffusion的过程密切相关。在diffusion的过程中，通过重参数的方法进行加噪，再经过一顿爆肝推导，得出q(xt−1∣xt,x0)∼ N(αˉt−1βtx0+αt(1−αˉt−1)xt1−αˉt,(1−αt)(1−αˉt−1)1−αˉt)q(x_{t-1}|x_{t}, x_{0})\sim N(\frac{\sqrt{\bar\alpha_{t-1}}\beta_{t}x_{0} + \sqrt{\alpha_{t}}(1-\bar\alpha_{t-1})x_{t}}{1 - \bar\alpha_{t}}, \frac{(1-\alpha_{t})(1-\bar\alpha_{t-1})}{1-\bar\alpha_{t}})，易看出该分布中方差是只和我们设置的超参数相关的常量。

（8）再来看（6）中的pθ(xt−1∣xt)p_{\theta}(x_{t-1} | x_{t})一项，下标说明了该项和模型相关。为了让p和q的分布接近，我们需要让p去学习q的均值和方差。由于方差是一个常量，在DDPM中，假设它是固定的，不再单独去学习它（后续的扩散模型，例如GLIDE则同时对方差也做了预测）。因此现在只需要学习q的均值。经过一顿变式，可以把q的均值改写成

1αt(xt−1−αt1−αˉtϵ) \frac{1}{\sqrt{\alpha_{t}}}(x_{t} - \frac{1-\alpha_{t}}{\sqrt{1-\bar\alpha_{t}}}\epsilon)。因此，这里只要让模型去预测噪声ϵθ\epsilon_{\theta}，使得ϵθ→ϵ\epsilon_{\theta}\to\epsilon，就能达到达到（1）中的目的！

七、参考

在学习DDPM的过程中，我也看了很多参考资料，但发现很难将整个推导过程串成一条符合思维惯性的逻辑链，因此对很多细节也是一知半解。直到我看到李宏毅老师对扩散模型原理的讲解（从分布相似性入手），以及阅读了google的一篇关于扩散模型数学推理的综述，才恍然大悟。自己动手推导后，从更符合我惯性思维的角度入手，写了这篇文章。因此，我也把我认为非常有帮助的参考资料列在下面，大家可以补充阅读。

1、李宏毅，扩散模型讲解：speech.ee.ntu.edu.tw/~hylee/ml/m…

2、Understanding Diffusion Models: A Unified Perspective：arxiv.org/pdf/2208.11…

3、DDPM：arxiv.org/pdf/2006.11…

4、重参数：spaces.ac.cn/archives/67…

avatar
文章
阅读
粉丝