我正在参加「掘金·启航计划」
本章我们将开始学习空间变换,空间变换在图形学中有非常广泛的应用,对于我们深入了解图形学底层有很重要的意义,特别在光栅化渲染管线中, 我们知道最初输入的顶点坐标都是物体局部空间的(LocalSpace), 需要经过一系列的变换将物体从局部空间变换为世界空间(物体摆放在场景的哪里,物体的相对位置关系),接下来再变换到相机空间(即我们观看的视角,就像拿个相机拍照一样,我们是从哪个角度对场景进行观察的),即mvp矩阵中的"m(model Matrix)和v(view Matrix)".这一系列操作即光栅化渲染管线的第一个阶段,也是理解光栅化背后原理的基础.本章将介绍涉及图形学的基础变换
空间变换(Spatial Transformation)
任何将一个点转换到一个新位置的函数都可以被认定为空间变换
f:Rn→Rn
今天我们将重点学习几种基本变换:
- 旋转(Rotation)
- 缩放(Scaling)
- 平移(Translation)(仿射变换)
- 错切(Shearing)
- 镜像("Reflect")
重点讲解 1. 空间几何表示 2. 矩阵表示 3.齐次坐标 4.如何用齐次坐标解决仿射变换和线性变换统一问题
线性变换回顾
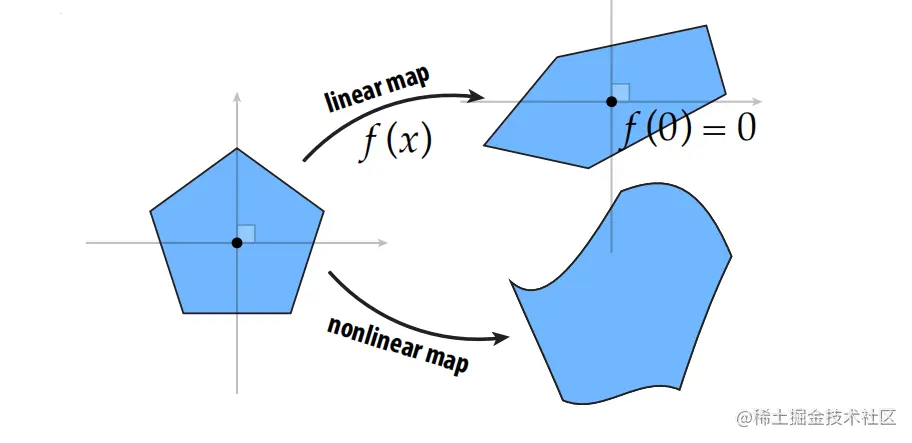
前几章我们详细阐述了线性变换的定义,并从几何上和代数上分别对其做了解释:
- 从几何的角度,线性变换会保持直线变换后仍然为直线,并保持原点不变
- 从代数角度:
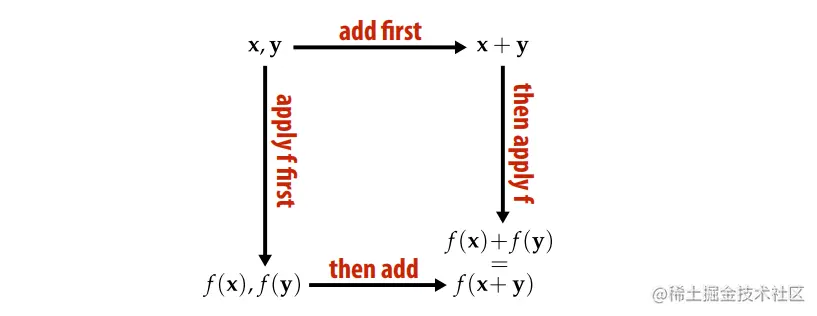
f(u+v)=f(u)+f(v)
f(au)=af(u)
为什么我们要关注线性变换?
- 应用成本低廉
- 容易求解
- 多个线性变换的符合构造仍然是线性的
- 多个线性变换的乘积可以用单个矩阵来表达
- 对各种变换提供了统一的表达方式
变换的种类
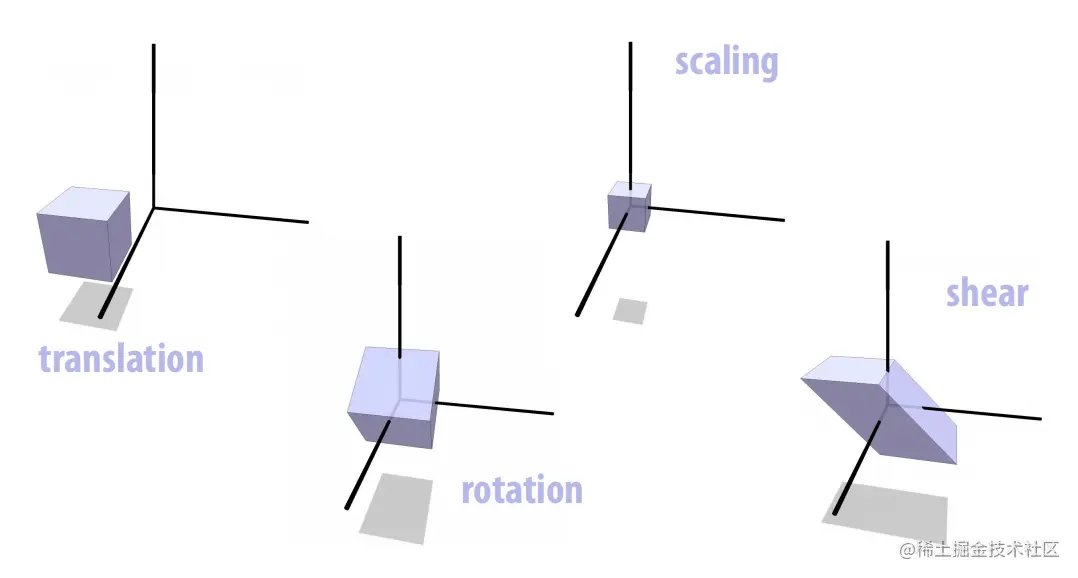
各种变换的特征(经过变换后哪些保持不变)
| 变换 | 不变性 | 代数描述 |
|---|
| 线性 | 直线保持直线 原点不变性 | f(ax+y)=af(x)+f(y), f(0)=0 |
| 平移 | 两点之间相对位置不变 | f(x−y)=x−y |
| 缩放 | 直线经过原点 任意一点的方向不变 | f(x)/∥f(x)∥=x/∥x∥ |
| 旋转 | 原点保持不变,两点之间距离不变,面的朝向不变 | ∥f(x)−f(y)∥=∥x−y∥,def(f)>0 |
旋转(Rotation)
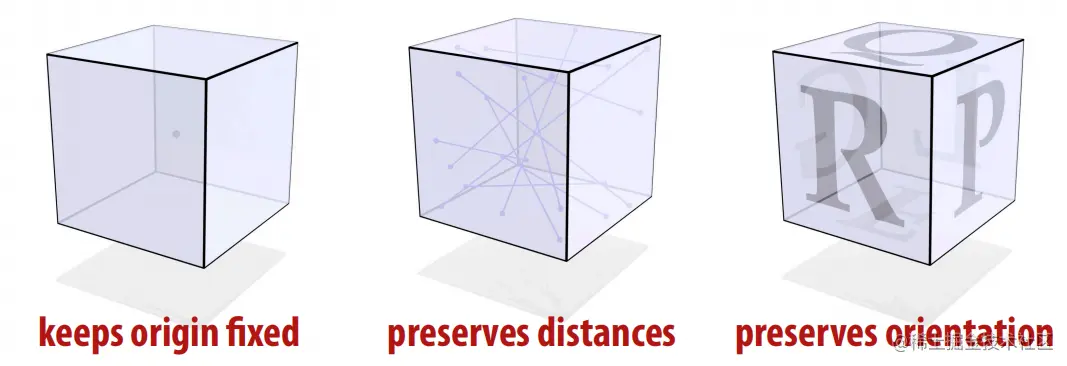 旋转有三个特征,保持原点不变,保持两点之间距离不变,保持面的朝向不变,前两个特征意味着旋转是一个线性变换
旋转有三个特征,保持原点不变,保持两点之间距离不变,保持面的朝向不变,前两个特征意味着旋转是一个线性变换
二维旋转
我们知道旋转保持距离和原点不变,因此,二维旋转(旋转角度θ)会将点x映射到同一半径的圆上的一点fθ(x)
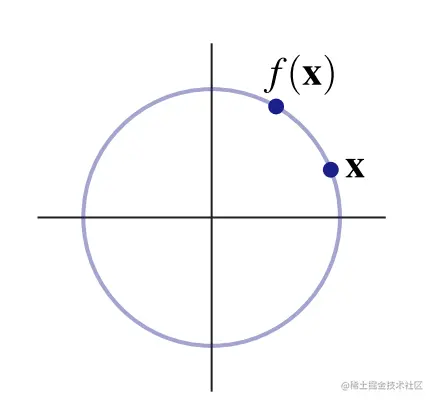
那么当点x位于(1,0)处时,逆时针旋转θ,点会被映射到哪里呢?
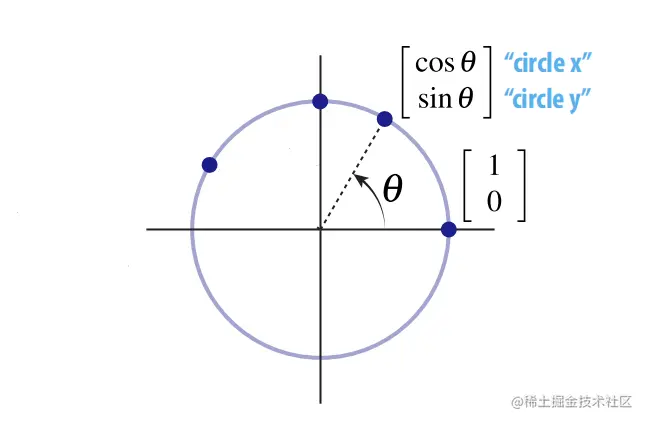
根据简单的三角函数可知,该点的坐标被旋转后为(cos(θ),sin(θ)).
同理当点位于(0,1)时,被旋转θ角后为(−sin(θ),cos(θ))
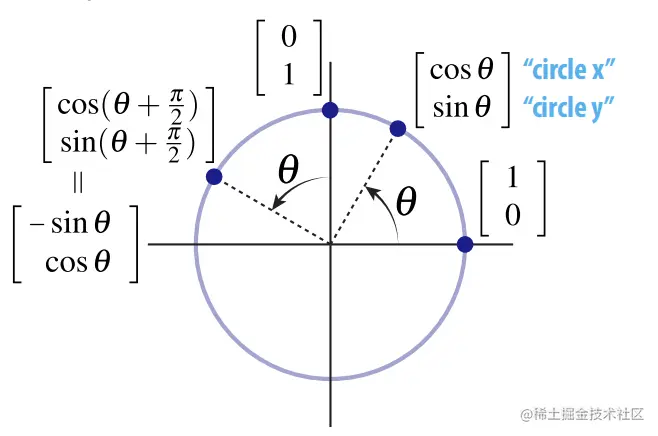
那么对于任意一个点(x,y),该怎么办呢?
我们可以将任意向量分解为两个基向量的线性组合:
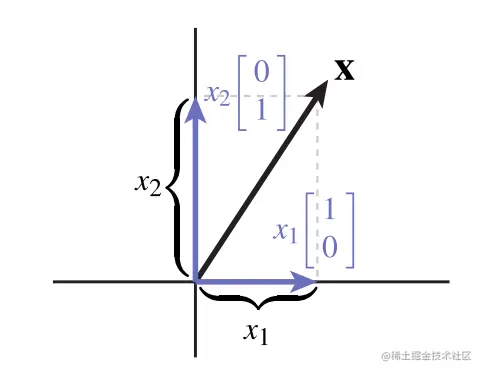
x=[x1x2]=x1[10]+x2[01]
通过上边的推导(特殊的两个点/basis),我们知道二维空间下基向量是如何旋转的,因此只需要简单的应用基向量的线性组合.
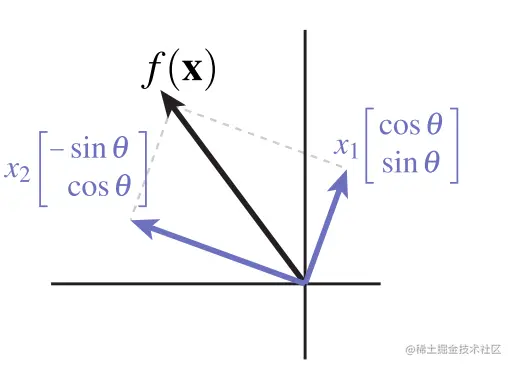
f(x)=x1[cos(θ)sin(θ)]+x2[−sin(θ)cos(θ)]
二维旋转的矩阵表示:
fθ(x)=[cos(θ)sin(θ)−sin(θ)cos(θ)]
三维旋转
在三维空间,如何围绕基向量Z旋转?只需要保持该基向量不变,其他应用二维变换即可:
⎣⎡cos(θ)sin(θ)0−sin(θ)cos(θ)0001⎦⎤
围绕X旋转:
⎣⎡1000cos(θ)sin(θ)0−sin(θ)cos(θ)⎦⎤
旋转矩阵: 矩阵的转置 = 矩阵的逆
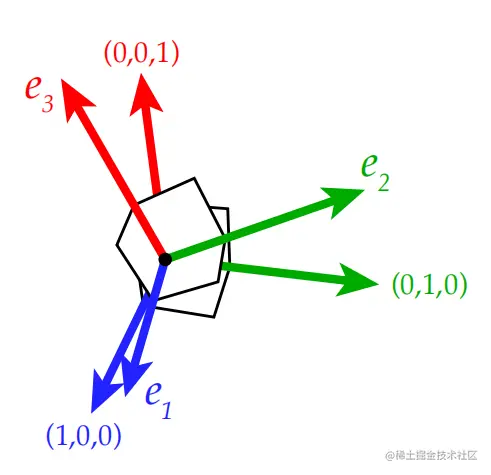
旋转会将标准正交基变换为另外一个正交基e1,e2,e3,旋转矩阵可以用正交基e1,e2,e3来表示,其中每个基向量做为旋转矩阵的一列,而矩阵的转置是将矩阵的每一列放到对应的行:
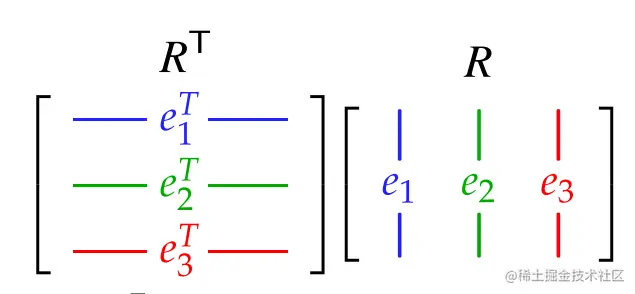
有趣的地方来了,当我们将两个矩阵相乘:

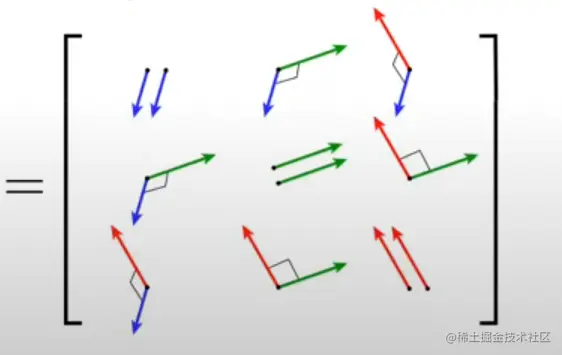
我们知道变换后的基向量是正交基(根据旋转矩阵的性质),根据正交基的定义,基向量相互垂直,推导出:
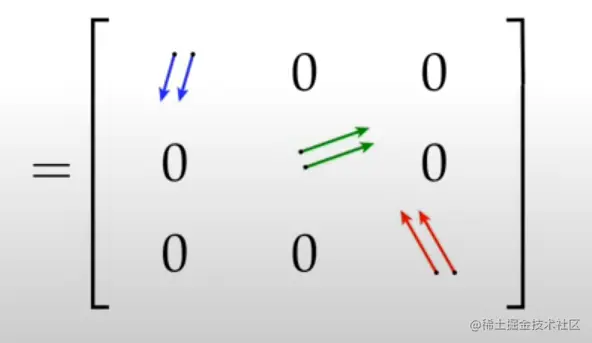
向量均为单位向量,长度为1,推导出:

重要结论
RTR=I
R−1R=I
RTR=R−1R
⟹RT=R−1
旋转矩阵的转置等于它的逆矩阵,这个结论为什么很有用呢,因为矩阵的逆比较难计算,而矩阵的转置相对计算廉价,因此我们可以利用旋转矩阵的这一特殊性质求它的逆矩阵:转置即可.
反射(Relection)
那么,任何满足QTQ=I的矩阵都是旋转矩阵吗?
考虑下边的矩阵:
Q=[−1001] QTQ=[(−1)2001]=I

那么Q是旋转矩阵吗?显然不是的,该矩阵描述了水平方向上的镜像变换,违反了旋转矩阵的面朝向不变性,是一个反射矩阵(Reflections)
正交矩阵(OrthogonalTransformations)
我们将这种类型的矩阵(保持距离和原点不变)称之为正交矩阵,旋转矩阵和反射矩阵都是正交矩阵的子集,代数表示:
QTQ=I
旋转矩阵: 除了保持距离和原点不变以外,还会保持朝向不变: det(Q)>0
反射矩阵: 反转朝向:det(Q)<0
本章我们深入了解了其中两种变换,旋转和反射,并将其推广到了更泛化的定义:正交矩阵,下一章我们将深入探讨缩放/错切/平移矩阵.
本系列文章会不定期更新,如果你觉得文章对你有帮助,可以订阅专栏计算机图形学,第一时间获取文章更新信息,也希望小伙伴们多多关注,多多点赞:)
旋转有三个特征,保持原点不变,保持两点之间距离不变,保持面的朝向不变,前两个特征意味着旋转是一个线性变换