线性规划

ARCTURUS
300 阅读6分钟

线性规划模型

生产计划问题

用 3 种原料混合配制 2 种清洁剂, 这 2 种清洁剂应 各配制多少 才能使总价值最大?

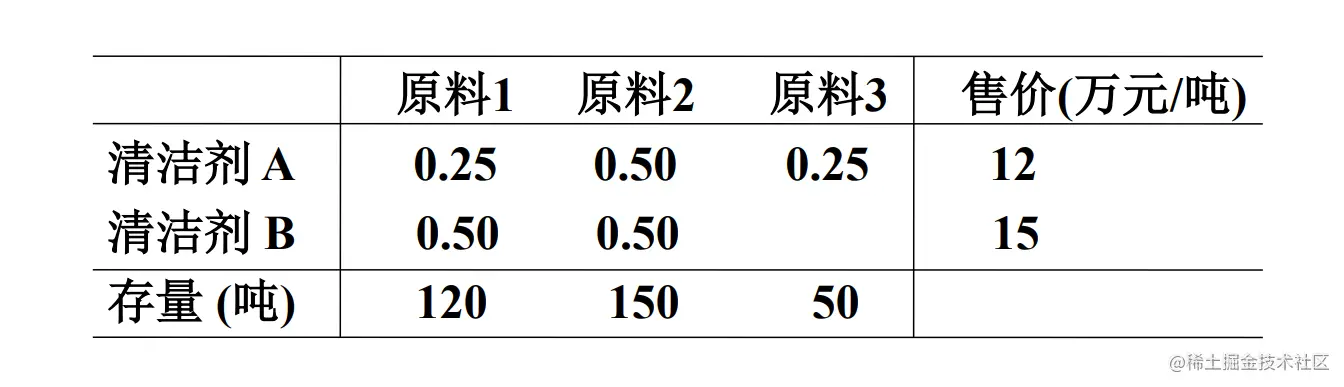
image.png

目标函数

max z=12x+15ymax\ z = 12x + 15y

约束条件(s.t.)

0.25x+0.50y≤1200.50x+0.50y≤1500.25x≤50x≥0,y≥0\begin{gathered} 0.25x + 0.50y \le 120\\ 0.50x + 0.50y \le 150\\ 0.25x \le 50\\ x \ge 0, y \ge 0 \end{gathered}

运输问题

产销平衡, 试制定供销方案, 使总运费最小?

image.png

目标函数

min z=3x11+2x12+7x13+7x21+5x22+2x23min\ z = 3x_{11} + 2x_{12} + 7x_{13} + 7x_{21} + 5x_{22} + 2x_{23}

约束条件

x11+x12+x13=5000x21+x22+x23=6000x11+x21=6000x12+x22=4000x13+x23=1000\begin{gathered} x_{11} + x_{12} + x_{13} = 5000\\ x_{21} + x_{22} + x_{23} = 6000\\ x_{11} + x_{21} = 6000\\ x_{12} + x_{22} = 4000\\ x_{13} + x_{23} = 1000 \end{gathered}

一般形式

min or max z=∑j=1ncjxjs.t. ∑j=1naijxj≥ or ≤ or =bixj≥0\begin{gathered} min\ or\ max\ z = \sum_{j=1}^n c_j x_j \\ s.t. \ \sum_{j=1}^na_{ij}x_j\ge\ or\ \le\ or \ = b_i \\ x_j\ge 0 \end{gathered}

  • 可行解 满足约束条件和非负条件的变量

  • 可行域 全体可行解

  • 最优解 目标函数值最小(最大)的可行解

  • 最优值 最优解的目标函数值

二维线性规划图解

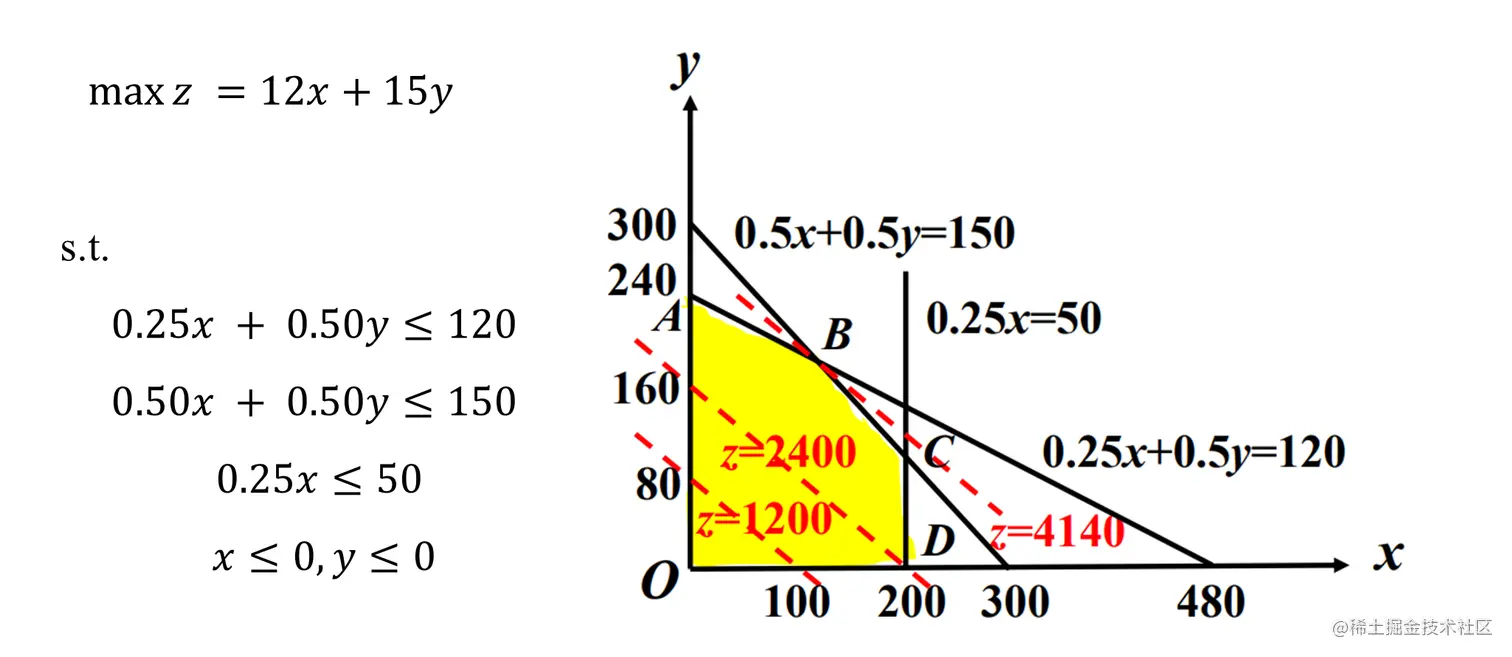
image.png

实际求解在取值范围内 12x+15y12x+15y 截距的最大值, 当与 BB 相切时截距最大, 即 x=120,y=180x=120, y=180

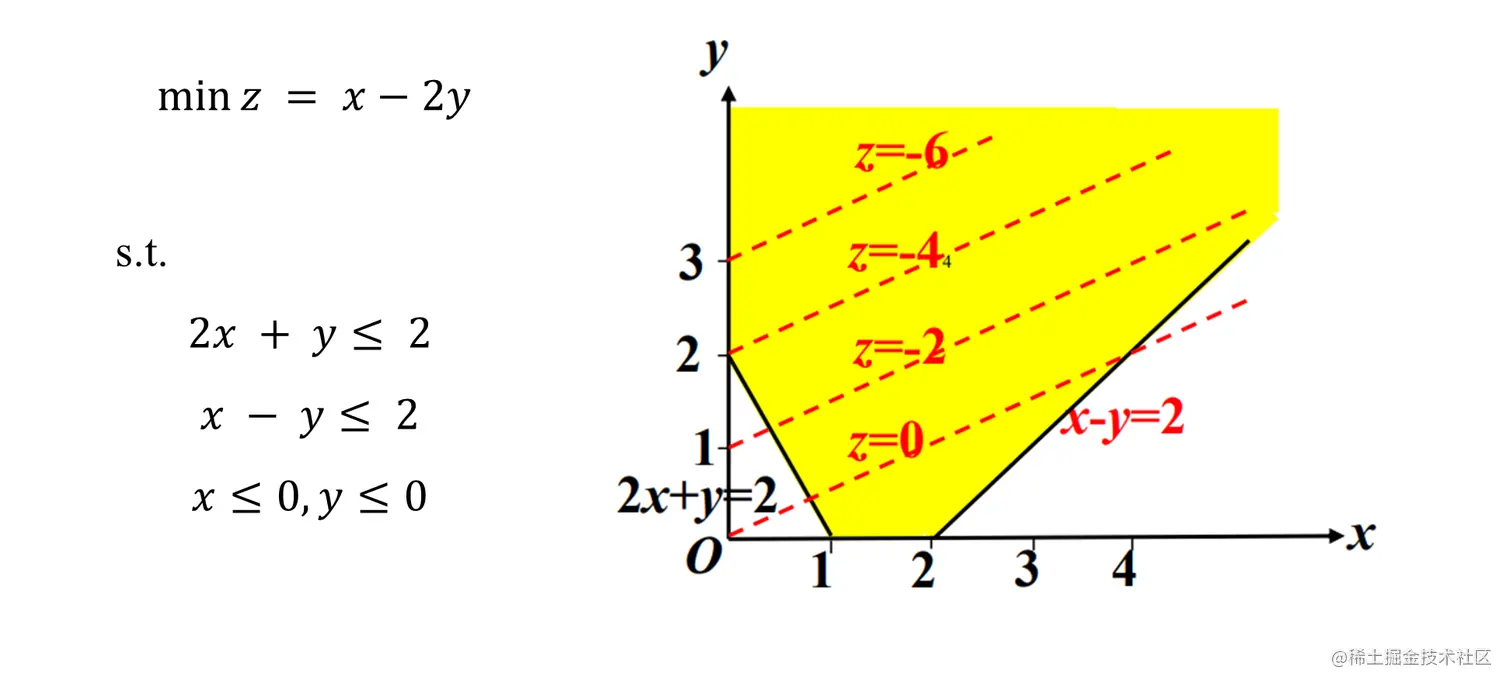
image.png

此时不存在最优解( z 可以无穷小下去 ), 可行解有无穷个

标准形

min z=∑j=1ncixis.t.∑j=1naijxj=bi≥0,i=1,2,⋯ ,mxj≥0,j=1,2,⋯ ,n\begin{gathered} min\ z = \sum_{j=1}^n c_ix_i \\ s.t. \sum_{j=1}^n a_{ij} x_j = b_i \ge 0, i = 1, 2, \cdots, m \\ x_j\ge 0, j = 1,2,\cdots,n \end{gathered}

转为标准型

  • maxmax 换成 minmin , 即 cj′=−cjc_j' = -c_j

  • ∑j=1naijxj≤bi\sum_{j=1}^n a_{ij}x_j \le b_i 引入松弛变量 yj≥0y_j\ge0 使得 ∑j=1naijxj+yj=bi\sum_{j=1}^n a_{ij}x_j + y_j = b_i

  • ∑j=1naijxj≥bi\sum_{j=1}^n a_{ij}x_j \ge b_i 引入剩余变量 yj≥0y_j\ge0 使得 ∑j=1naijxj−yj=bi\sum_{j=1}^n a_{ij}x_j - y_j = b_i

  • 自由变量 xjx_j 变为 xj′−xj′′x_j'-x_j'' , xj′≥0,xj′′≥0x_j' \ge 0, x_j'' \ge 0

因为标准形中要求变量非负, 因此自由变量写成减法的形式, 即 xj=xj′−xj′′x_j=x_j'-x_j'' , 这样就可以要求两个新变量都是正数, 若已知 xj≥0x_j \ge 0 , 则不需要这样转

例子

max z=3x1−2x2+x3max\ z = 3x_1 − 2x_2 + x_3
x1+3x2−3x3≤104x1−x2−5x3≤−30x1≥0,x2≥0,x3\begin{gathered} x_1 + 3x_2 − 3x_3 \le 10 \\ 4x_1 − x_2 − 5x_3 \le -30 \\ x_1 \ge 0, x_2 \ge 0, x_3 \end{gathered}

转化为标准型后为

注意这里 x3x_3 没有明确是正数还是负数, 因此需要转为 xj′−xj′′x_j'-x_j''

min z=−3x1+2x2−x3′+x3′′x1+3x2−3x3′+3x3′′+x4=10−4x1+x2+5x3′−5x3′′−x5=30x1≥0,x2≥0,x3′≥0,x3′′≥0,x4≥0,x5≥0\begin{gathered} min\ z = -3x_1 + 2x_2 - x_3' + x_3'' \\ x_1 + 3x_2-3x_3' + 3x_3'' + x_4 = 10 \\ -4x_1 + x_2 + 5x_3' - 5x_3'' - x_5 = 30 \\ x_1 \ge 0, x_2 \ge 0, x_3' \ge 0, x_3'' \ge 0, x_4 \ge 0, x_5 \ge 0 \end{gathered}

标准形矩阵

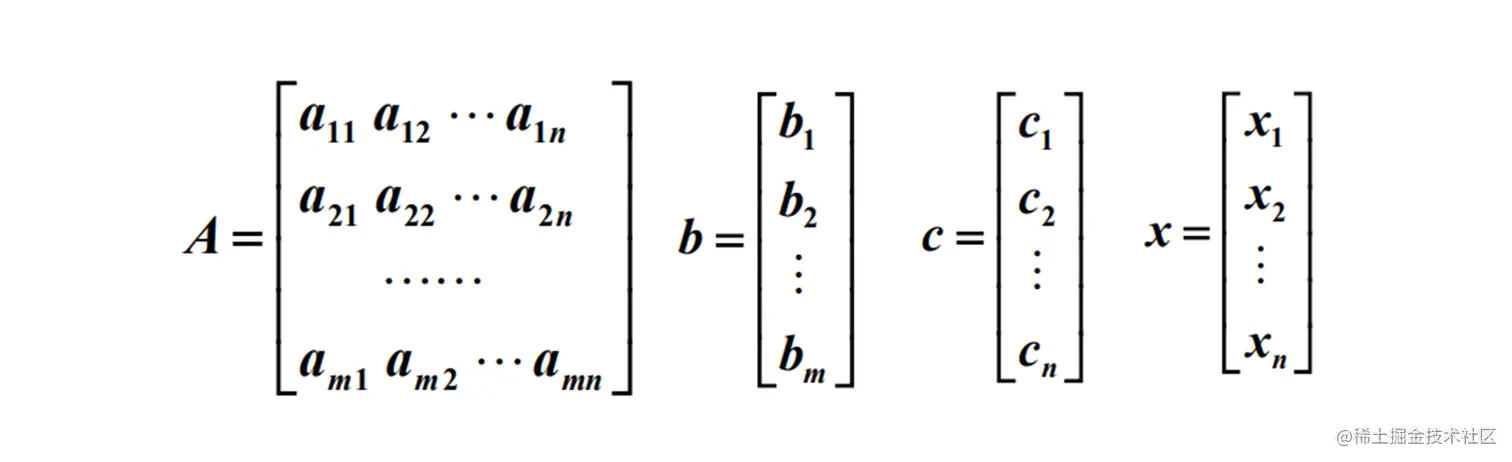
image.png

image.png

min z=cTxs.t. Ax=b or ∑j=1nPjxj=bx≥0\begin{gathered} min\ z = c^Tx \\ s.t. \ Ax = b\ or\ \sum_{j=1}^n P_jx_j = b \\ x \ge 0 \end{gathered}

可行解性质

设 AA 的秩为 mm, AA 的 mm 个 线性无关 的列向量称作标准形的 基 , 给定基 B=(P1,P2,⋯ ,Pm)B=(P_1, P_2, \cdots, P_m) , 对应基中列向量的变量 x1,x2,⋯ ,xmx_1, x_2, \cdots, x_m, 称作 基变量 , 其余的变量称作 非基变量

基变量构成的向量记作 xBx_B , 非基变量构成的向量记作 xNx_N, 令 xN=0x_N = 0 , 约束条件变成 BxB=bBx_B = b , 解得 xB=B−1bx_B = B^{-1}b , 这个向量 xx 满足约束 Ax=bAx=b 且非基变量 全为 0 , 称作关于基 BB 的 基本解

如果 xx 是一个基本解且 x≥0x \ge 0 , 则称 xx 是一个 基本可行解 , 对应的基 B 为 可行基

例子

min z=−12x1−15x2min\ z = −12x_1 − 15x_2
0.25x1+0.50x2+x3=1200.50x1+0.50x2+x4=1500.25x1+x5=50\begin{aligned} 0.25x_1 + 0.50x_2 + x_3 &= 120 \\ 0.50x_1 +0.50x_2 + x_4 &= 150 \\ 0.25x_1 + x_5 &= 50 \end{aligned}
xi≥0,i=1,2,⋯ ,5x_i \ge 0, i = 1,2,\cdots,5

image.png

取基 B1=(P1,P2,P3)B_1=(P_1,P_2,P_3) , 基变量 x1,x2,x3x_1, x_2, x_3 , 非基变量 x4,x5x_4, x_5 , 令 x4=0,x5=0x_4=0, x_5=0

image.png

解得 x1=200,x2=100,x3=20x_1=200, x_2=100, x_3=20 , x(1)=(200,100,20,0,0)Tx^{(1)}=(200,100,20,0,0)^T 是 基本可行解 ( 要求 xi≥0x_i \ge 0 ), B1B_1 是可行基

若取基 B2=(P1,P2,P4)B_2=(P_1, P_2, P_4) , 则

image.png

解得 x(2)=(200,140,0,−20,0)x^{(2)}=(200, 140, 0, -20, 0) 是一个基本解, 但不是基本可行解, 因此 B2B_2 不是可行基

定理

Ax=bAx = b 的解 α\alpha 是基本解, 当且仅当 α\alpha 中非零分量对应的列向量线性无关

  • 如果标准形有可行解, 则必有基本可行解

  • 如果标准形有最优解, 则必存在一个基本可行解是最优解

  • AA 有 mm 行 nn 列, 也就是说秩最多为 mm, 至多有 CnmC_n^m 个基(本解) , 即从 nn 列中取 mm 列组合为基

单纯形法

初始基本可行解

max z=12x+15ymax\ z = 12x + 15y
0.25x+0.5y≤1200.5x+0.5y≤1500.25x≤50x≥0y≥0\begin{aligned} 0.25x+0.5y &\le 120 \\ 0.5x+0.5y &\le 150 \\ 0.25x &\le 50 \\ x &\ge 0 \\ y &\ge 0 \end{aligned}

化为标准形后

min z′=−12x−15ymin\ z' = -12x - 15y
0.25x1+0.50x2+x3=1200.50x1+0.50x2+x4=1500.25x1+x5=50xi≥0\begin{aligned} 0.25x_1+0.50x_2+x_3 &= 120 \\ 0.50x_1+0.50x_2+x_4 &= 150 \\ 0.25x_1+x_5 &= 50 \\ x_i &\ge 0 \end{aligned}

若取基变量为 x3,x4,x5x_3, x_4, x_5 , 实际上初始可行基为 单位矩阵

image.png

则初始基本可行解为 x(0)=(0,0,120,150,50)Tx^{(0)}=(0,0,120,150,50)^T

最优性检验

给定可行基 B=(P1,P2,⋯ ,Pm)B=(P_1, P_2, \cdots, P_m)

对于约束条件 Ax=bAx=b 两边同时乘上 B−1B^{-1} 得到

B−1Ax=B−1bB^{-1}Ax=B^{-1}b

假设 AA 中对应非基变量的列构成的矩阵为 NN , 则有

xB+B−1NxN=B−1bx_B+B^{-1}Nx_N=B^{-1}b

注意 AA 中基变量对应的矩阵为 BB , 因此 B−1BxB=xBB^{-1}Bx_B=x_B

解得

xB=B−1b−B−1NxNx_B=B^{-1}b-B^{-1}Nx_N

将上述式子带入目标函数 z=cTxz=c^Tx 得

z=cTx=cBTxB+cNTxN=cBT(B−1b−B−1NxN)+cNTxN=cBTB−1b+(cNT−cBTB−1N)xN\begin{aligned} z &= c^Tx \\ \\ &= c_B^Tx_B + c_N^Tx_N \\ \\ &= c_B^T(B^{-1}b-B^{-1}Nx_N) + c_N^Tx_N \\ \\ &= c_B^TB^{-1}b + (c_N^T-c_B^TB^{-1}N)x_N \end{aligned}

由于基本可行解为 xB(0)=B−1b,xN(0)=0x_B^{(0)}=B^{-1}b, x_N^{(0)}=0 , 因此目标函数值为

z0=cBTB−1bz_0 = c_B^TB^{-1}b

因此目标函数可以变为

z=cTx=z0+(cNT−cBTB−1N)xN=z0+(cBT−cBTB−1B)xB+(cNT−cBTB−1N)xN=z0+(cT−cBTB−1A)x\begin{aligned} z &= c^Tx \\ \\ &= z_0 + (c_N^T-c_B^TB^{-1}N)x_N \\ \\ &= z_0 + (c_B^T-c_B^TB^{-1}B)x_B + (c_N^T-c_B^TB^{-1}N)x_N \\ \\ &= z_0 + (c^T-c_B^TB^{-1}A)x \end{aligned}

令检验数为

λT=cT−cBTB−1A\lambda^T=c^T-c_B^TB^{-1}A

目标函数变为

z=z0+λTxz=z_0 + \lambda^Tx

若 λi≥0\lambda_i \ge 0 , 则 x(0)x^{(0)} 是最优解

若存在 λk<0\lambda_k \lt 0 且所有 aik≤0(1≤i≤m)a_{ik} \le 0(1 \le i \le m) ( mm 是秩 ) , 则无最优解

基变换

令 Pj′=B−1Pj(1≤j≤n)P_j'=B^{-1}P_j(1\le j\le n) , A=(P1,P2,⋯ ,Pn)A=(P_1, P_2, \cdots, P_n)

设 λk<0\lambda_k\lt 0 且 alk>0a_{lk}\gt 0 , 其中 xkx_k 必是非基变量

用非基变量 xkx_k 替换基变量 xlx_l , 用 PkP_k 代替 BB 中的 PlP_l

因为 P1,P2,⋯ ,PmP_1, P_2, \cdots, P_m 线性无关, 因此可以表示 PkP_k, 即

Pk=∑i=1mαikPiP_k=\sum_{i=1}^m \alpha_{ik} P_i

解得

Pl=1alkPk−∑i=1,i≠lmaikalkPiP_l = \frac{1}{a_{lk}}P_k - \sum_{i=1, i\neq l}^m\frac{a_ik}{a_{lk}}P_i

由于 PlP_l 是 B′B' 的一个线性组合, 因此得到的 B′B' 依旧是一个基

要保证 B′B' 是一个可行基, 把它化为 单位矩阵 形式的同时需满足

βi′=βi−αikβlαlk≥0\beta_i' = \beta_i - \frac{\alpha_{ik}\beta_l}{\alpha_{lk}} \ge 0

当 αik≤0\alpha_{ik}\le 0 时必然成立, 当 αik>0\alpha_{ik}\gt0 时要求

βlαlk≤βiαik\frac{\beta_l}{\alpha_{lk}} \le \frac{\beta_i}{\alpha_{ik}}

因此可以选取

θ=βlαlk=min{βiαik∣αik>0,1≤i≤m}\theta=\frac{\beta_l}{\alpha_{lk}} = min\left\{\frac{\beta_i}{\alpha_{ik}}\lvert\alpha_{ik}\gt0, 1\le i\le m\right\}

单纯形法步骤

  1. 设初始可行基 B=(P1,P2,⋯ ,Pm)B = (P_1, P_2, \cdots, P_m) , λT=cT−cBTB−1A\lambda^T = c^T−c_B^TB^{−1}A

  2. 若所有 λj≥0(1≥j≥n)\lambda_j \ge 0 (1 \ge j \ge n) , 则 xB=β,xN=0x_B = \beta, x_N=0 是最优解(最小值)

  3. 若 λk<0\lambda_k \lt 0 且所有 αik≤0(1≤i≤m)\alpha_{ik} \le 0(1 \le i \le m) , 则无最优解 ( 即 λk<0\lambda_k < 0 且 AA 矩阵第 kk 列全是小于等于 0 的 )

  4. 做基变换, 继续判断 λj\lambda_j

若判断 最大值 , 则 λj≤0(1≥j≥n)\lambda_j \le 0 (1 \ge j \ge n) , λk>0\lambda_k \gt 0

单纯形表

对于线性规划

max z=12x+15ymax\ z = 12x + 15y
0.25x+0.5y≤1200.5x+0.5y≤1500.25x≤50\begin{aligned} 0.25x+0.5y &\le 120 \\ 0.5x+0.5y &\le 150 \\ 0.25x &\le 50 \\ \end{aligned}

转化为标准形后得

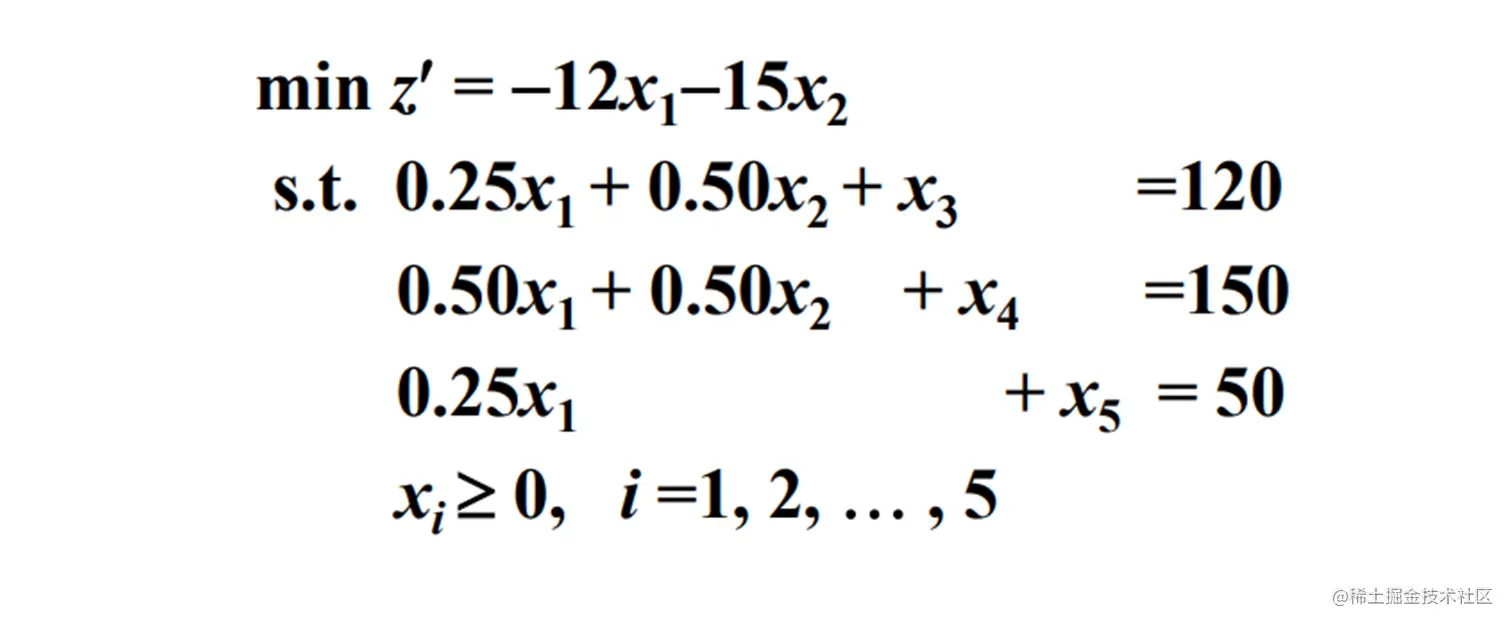
image.png

取基 B=(P3,P4,P5)B=(P_3, P_4, P_5) , 则

image.png

其中 β=B−1b\beta=B^{-1}b , 由于 BB 是单位矩阵, 因此

β=Bβ=BB−1b=b\beta = B\beta = BB^{-1}b=b

由 z0=cBTB−1b=cBTβz_0=c_B^TB^{-1}b=c_B^T\beta 可知

−z0=−(0×120+0×150+0×50)=0-z_0 = -(0×120+0×150+0×50)=0

由于初始时 cBT=0c_B^T=0 , 因此

λT=cT−cBTB−1A=cT\lambda^T=c^T-c^T_BB^{-1}A=c^T

由上图可知, 不存在全部 λ\lambda 都大于 00 , 因此 z0z_0 不是最优解 , 由于 λ1\lambda_1 和 λ2\lambda_2 均小于 00 , 但是 AA 的第一、第二列均不小于 00 , 因此可能存在最优解, 需要进行 基变换

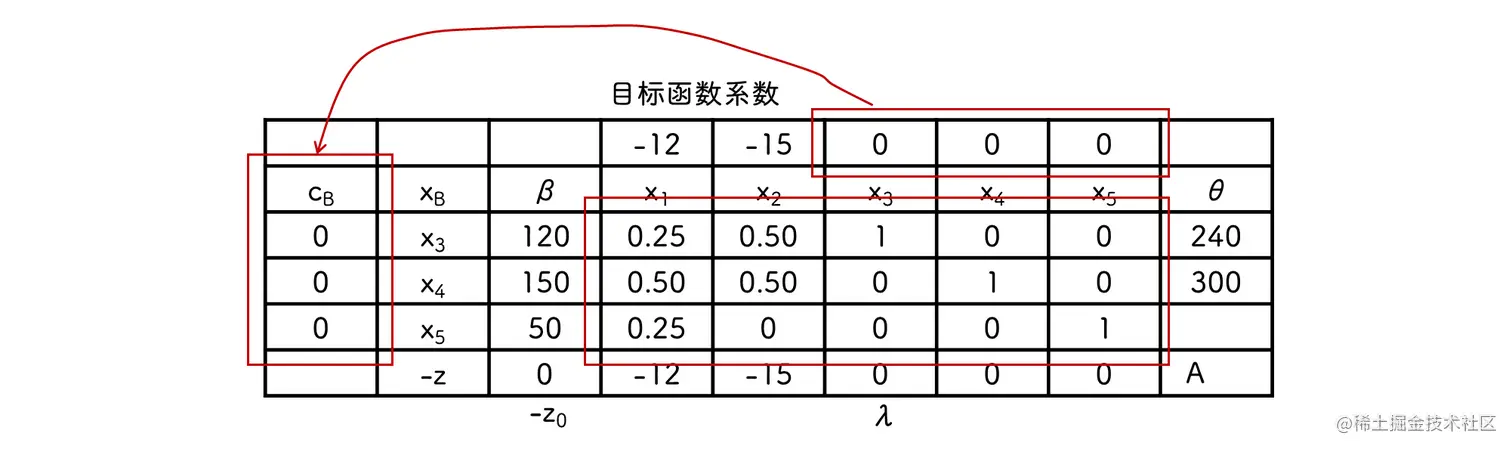
选取一个最小的 λ\lambda 进行基变换, 如上图 λ2\lambda_2 所在列

由于 θ=βlαlk\theta=\frac{\beta_l}{\alpha_{lk}} , 需要取 θ\theta 最小的列进行替换, 即 P3P_3 替换成 P2P_2

取基 B=(P2,P4,P5)B=(P_2, P_4, P_5)

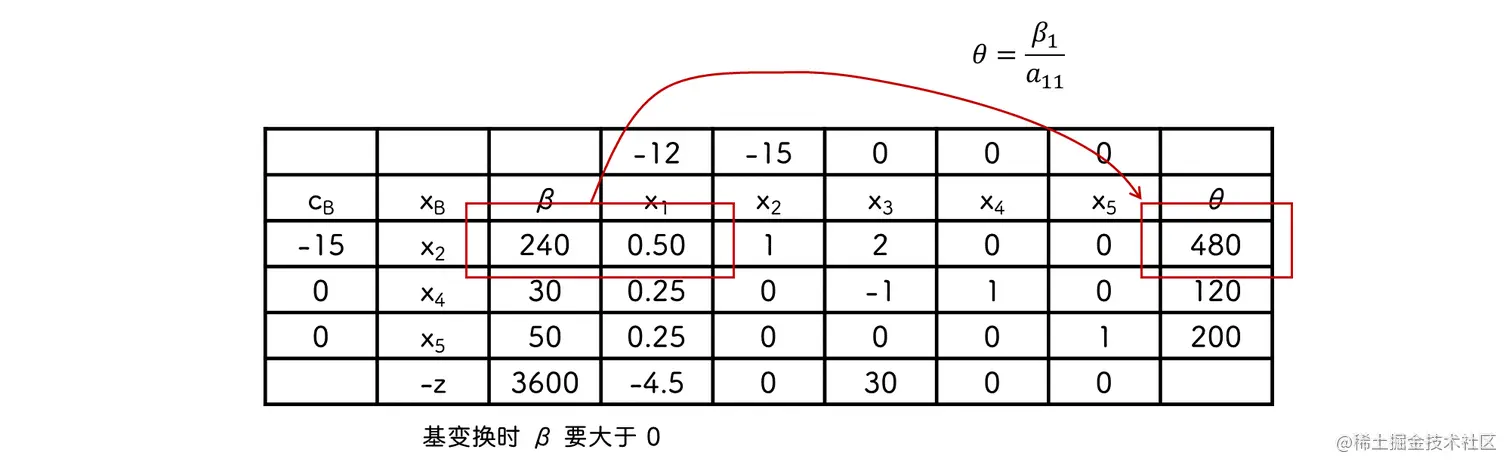
image.png

λ\lambda 可以直接变换, 也可以使用公式计算, 直接变换时使 λk=0\lambda_k=0 即可

由于依旧有 λ<0\lambda<0 , 因此再次进行变换, 使用 P1P_1 替换 P4P_4

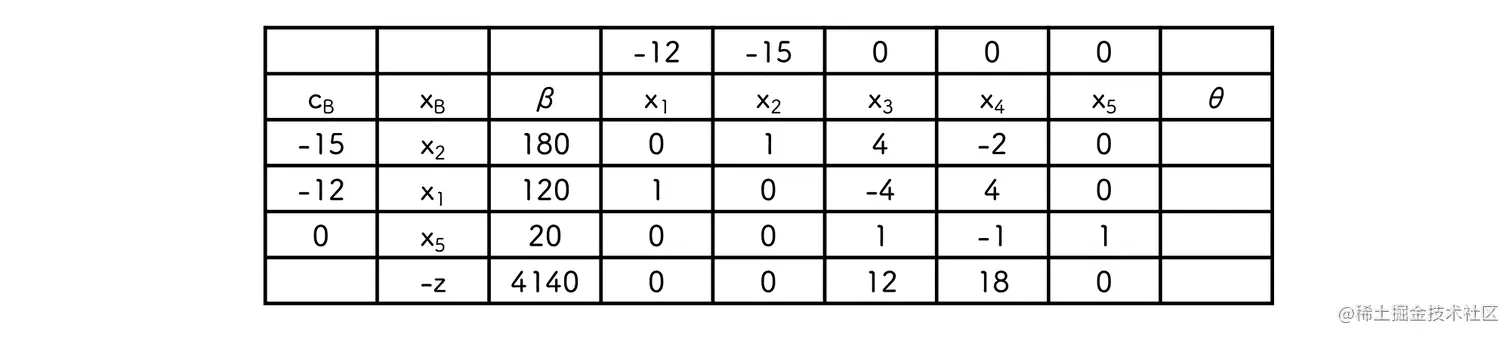
image.png

最优值为 z′=−4140z'=-4140 , 最优值 z=4140z=4140 , 最优解为 x1=120,x2=180x_1=120, x_2=180

无最优解的情况

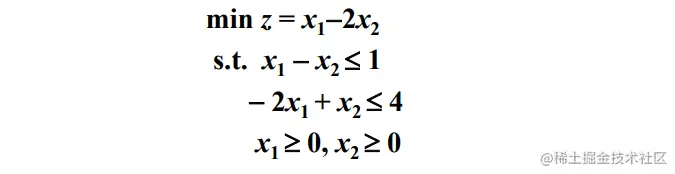
image.png

两个约束条件, 添加两个松弛变量 x3,x4x_3, x_4

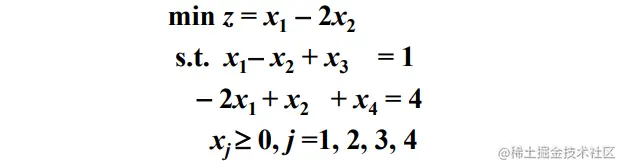
image.png

构造单纯形表

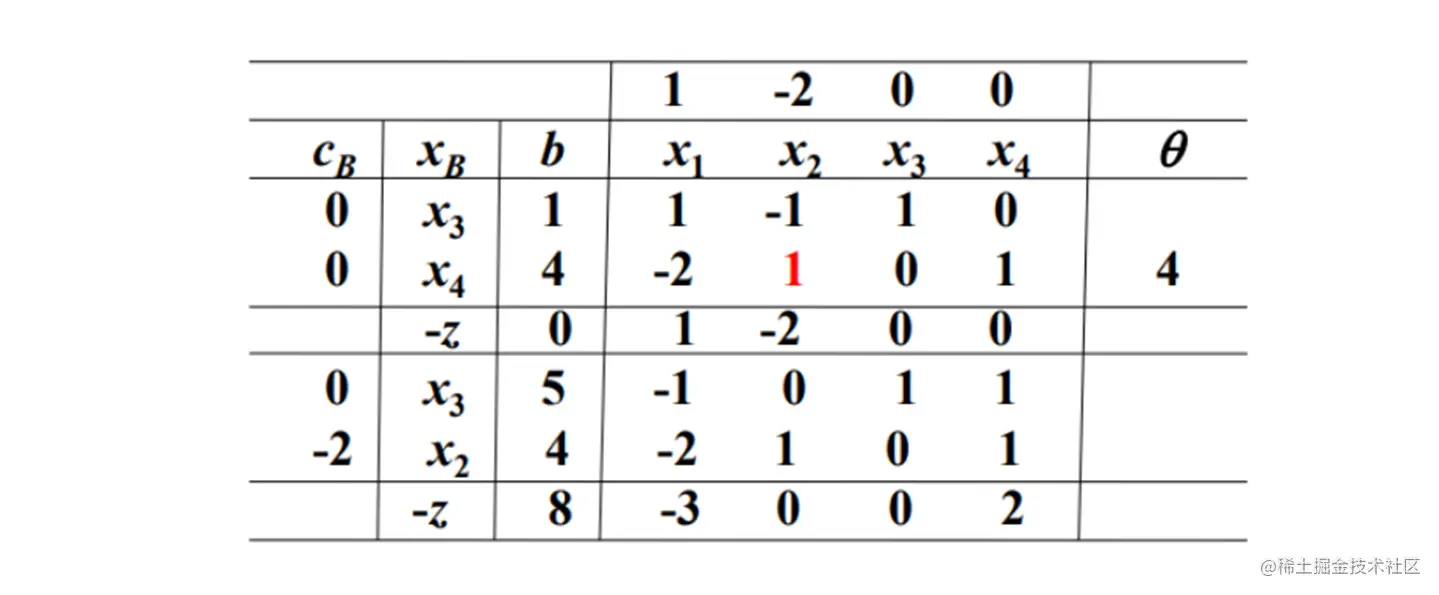
image.png

由于 λ1<0\lambda_1 < 0 且 (a11,a12)T<0(a_{11}, a_{12})^T < 0 因此无最优解

两阶段法

约束函数存在大于或等于的情况时

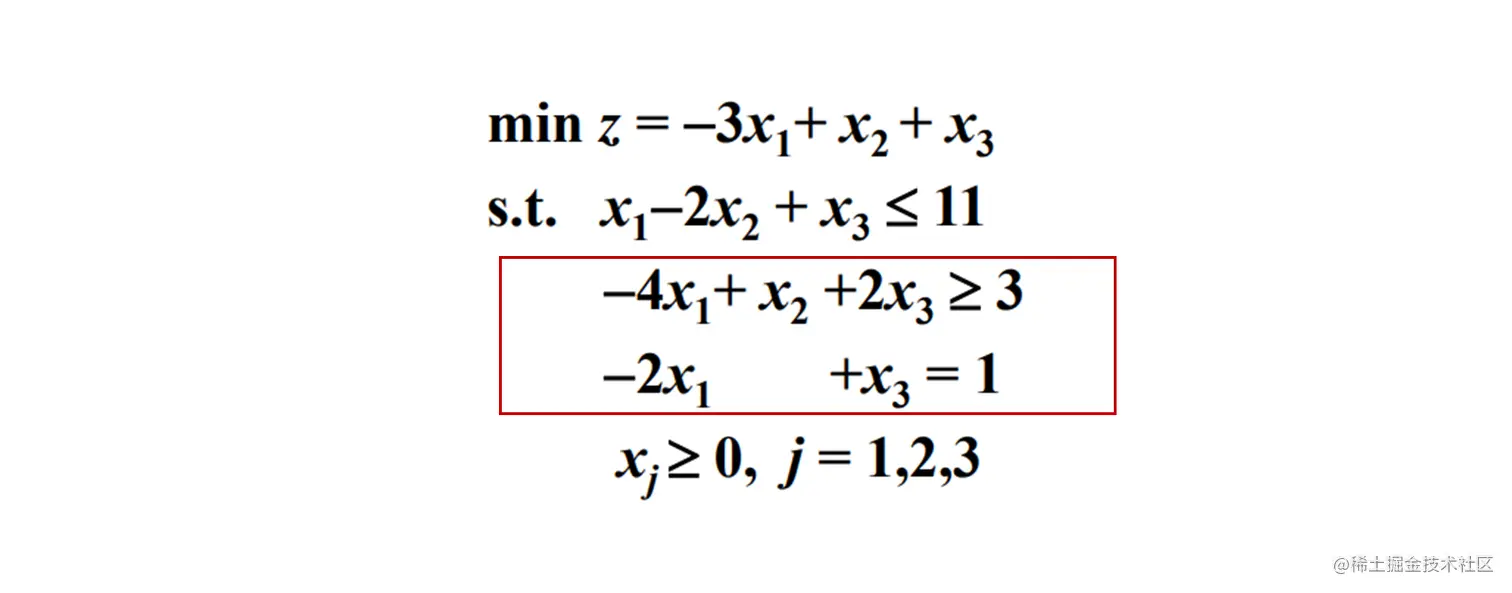
image.png

引入松弛变量 x4x_4 和剩余变量 x5x_5 转换为标准形

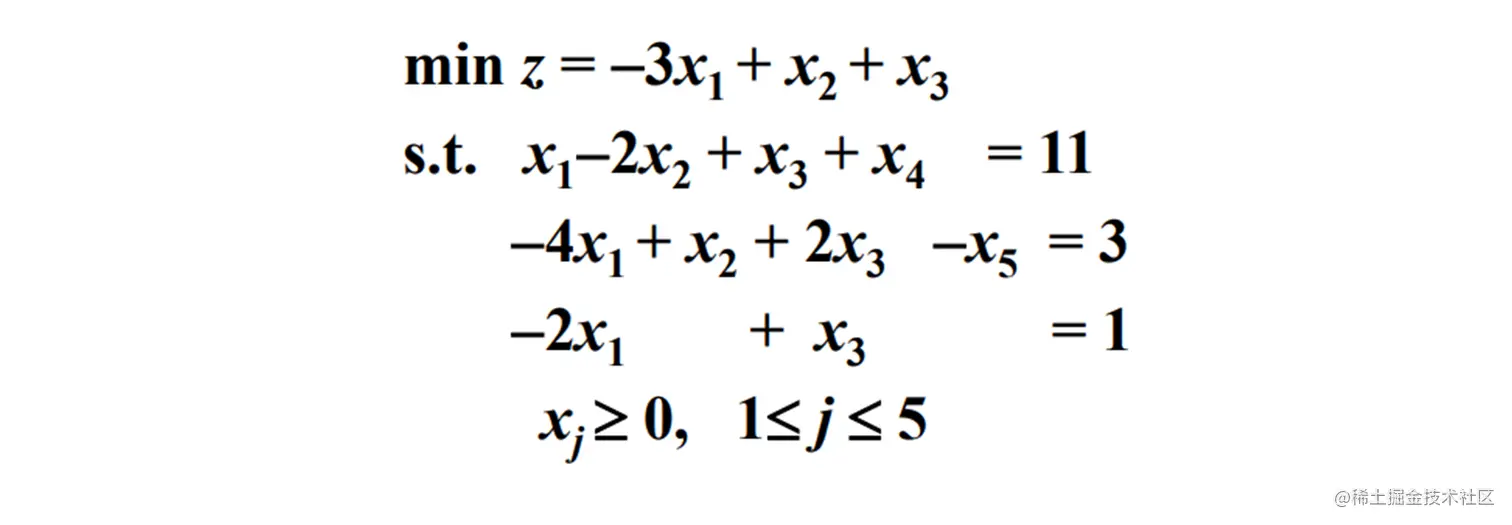
image.png

对于大于等于的情况, 还需要再引入人工变量 x6,x7x_6, x_7 ( 不是标准形了 )

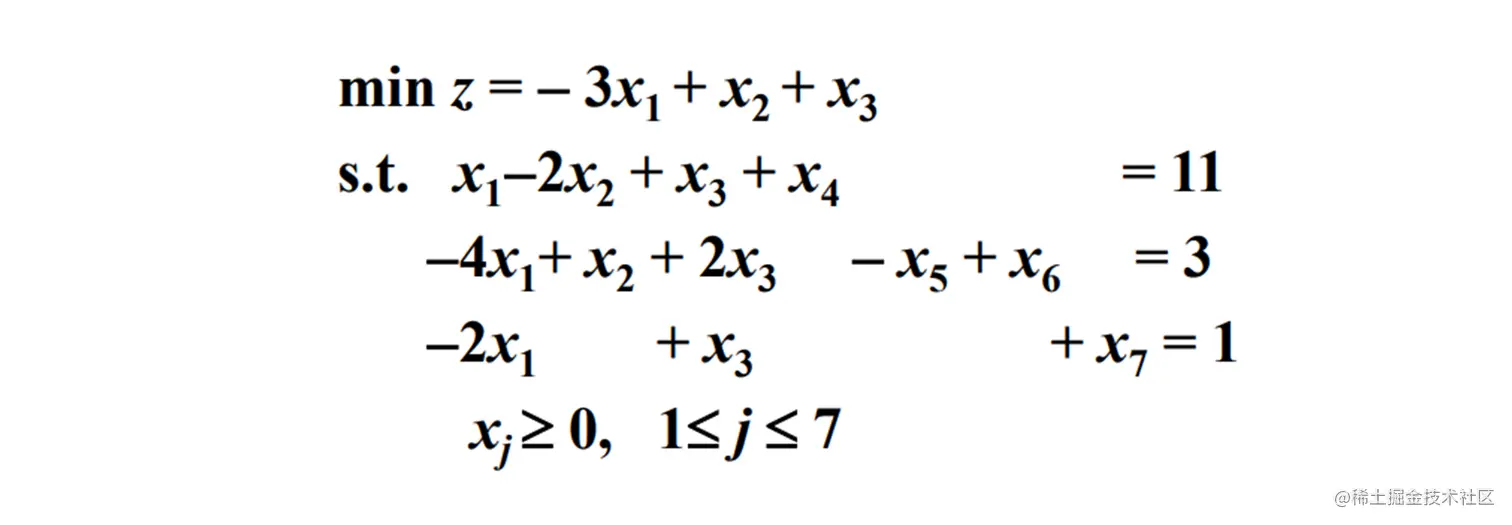
image.png

初始可行基 B=(P4,P6,P7)B=(P_4, P_6, P_7) , x(0)=(0,0,0,11,0,3,1)Tx^{(0)}=(0,0,0,11,0,3,1)^T

x(0)x^{(0)} 不是标准形的可行解, 只有当所有人工变量等于 00 时, 才能舍去人工变量得到标准形的可行解

对人工变量构造 辅助问题

min w=∑i=1myimin\ w = \sum_{i=1}^m y_i
s.t. ∑j=1naijxj+yi=bi,1≤i≤ms.t.\ \sum_{j=1}^n a_{ij}x_j+y_i=b_i, 1\le i \le m

假设辅助问题的最优解 w∗w^* , 存在三种情况

  1. 如果 w∗>0w^*>0 , 原问题无可行解

  2. 如果在最优解中, 所有的人工变量都是非基变量, 因此 w∗=0w^*=0 , 可以删除人工变量, 得到问题的解

  3. w∗=0w^*=0 , 但是人工变量不全是非基变量, 可以转化为 2

步骤

阶段一, 引入人工变量, 按照单纯形法求解 辅助问题 的最优值

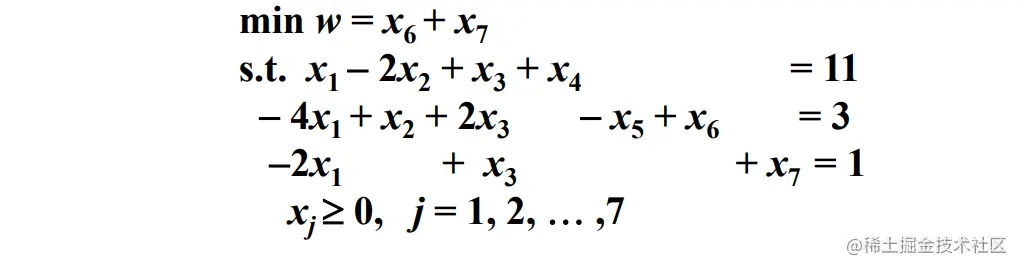
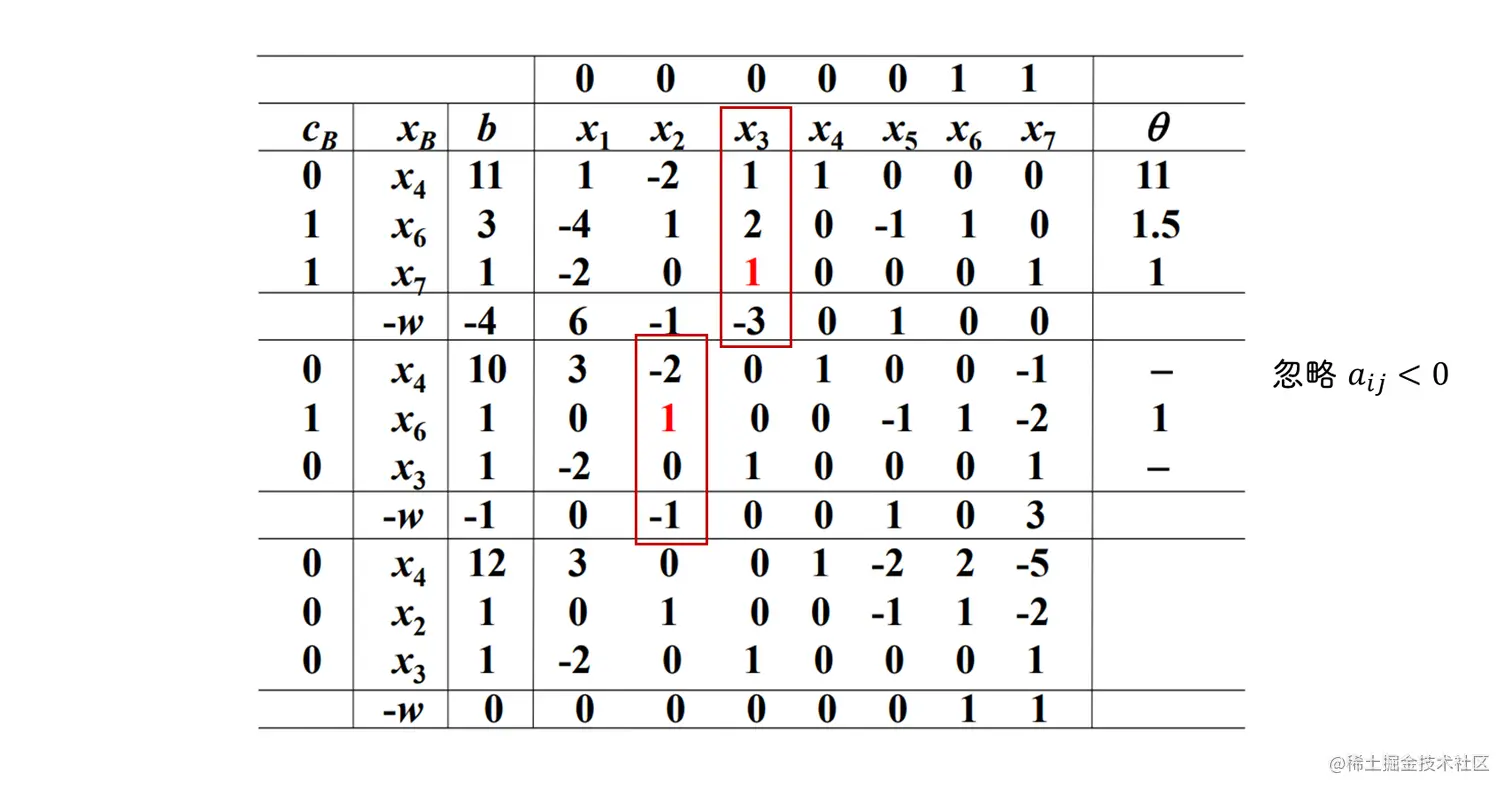
image.png

image.png

最优值 w∗=0w^*=0 , 且基变量为 x4,x2,x3x_4,x_2,x_3 均不是人工变量, 属于 情况二 , 进入阶段二

阶段二, 删除人工变量 x6,x7x_6, x_7

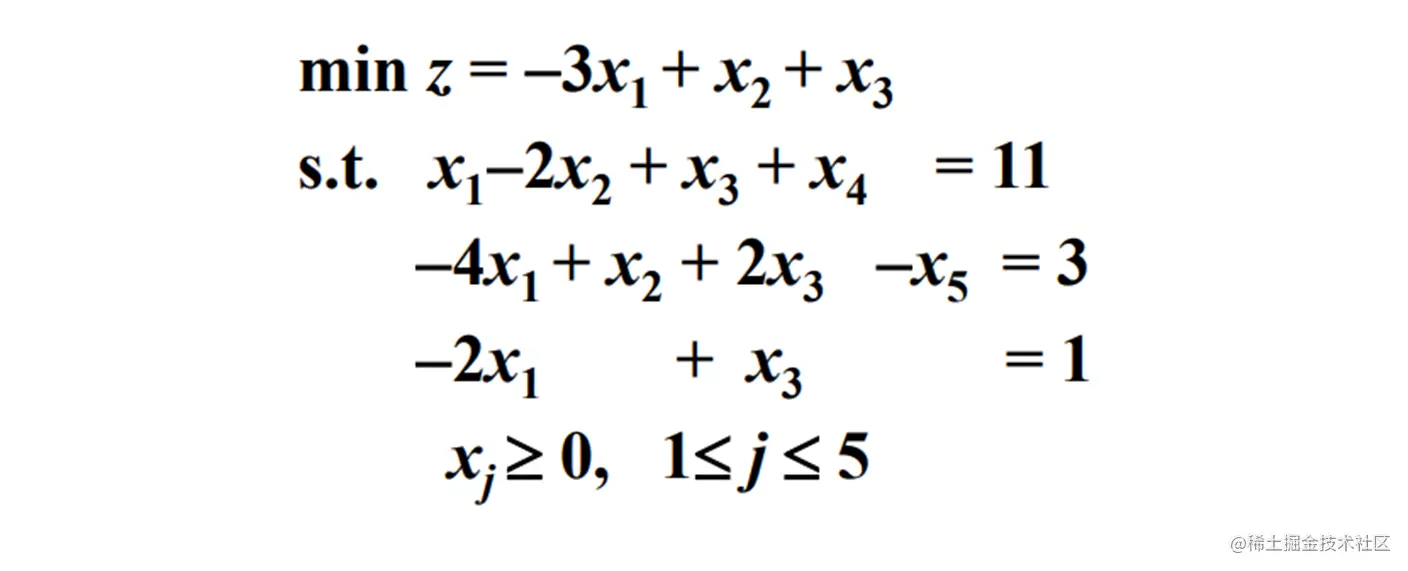
image.png

AA 和 β\beta 保持, 修改 cc 和 cBc_B

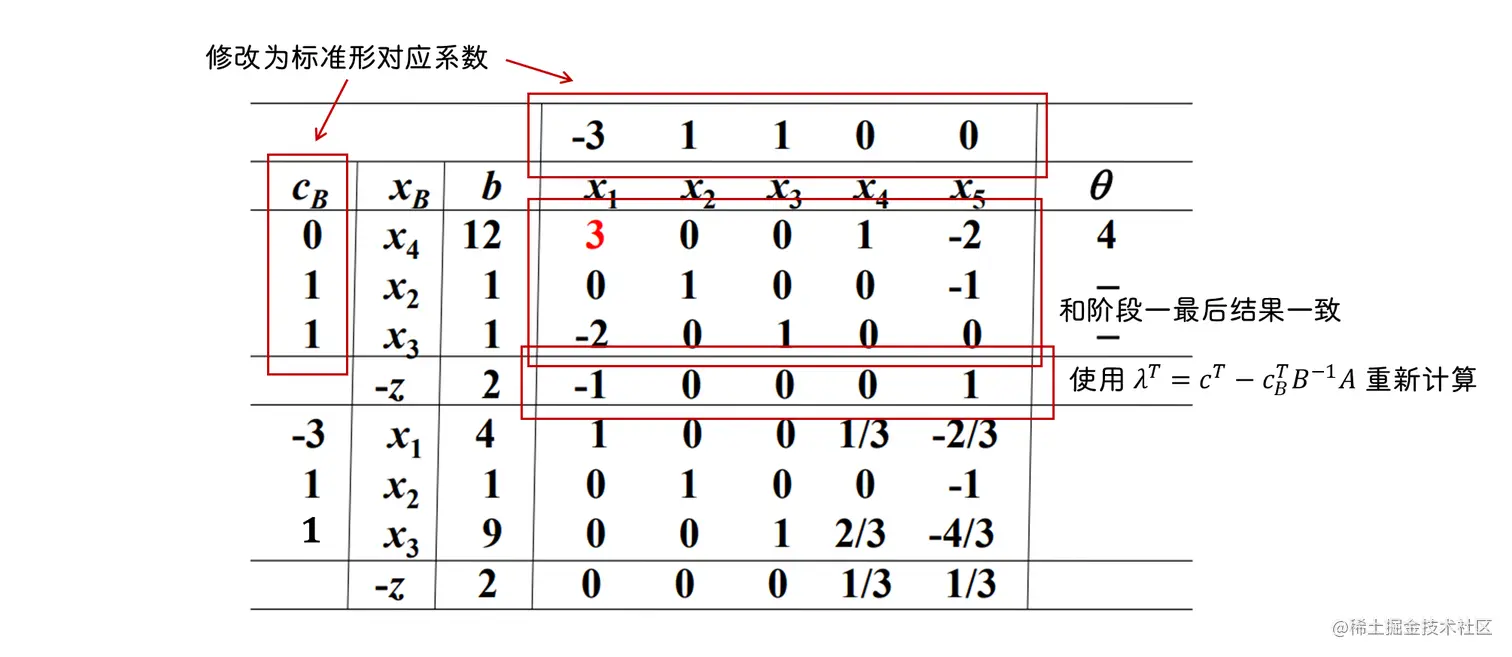
image.png

最优值 z=−2z=-2 , 最优解为 x1=4,x2=1,x3=9x_1=4, x_2=1, x_3=9

无解的情况

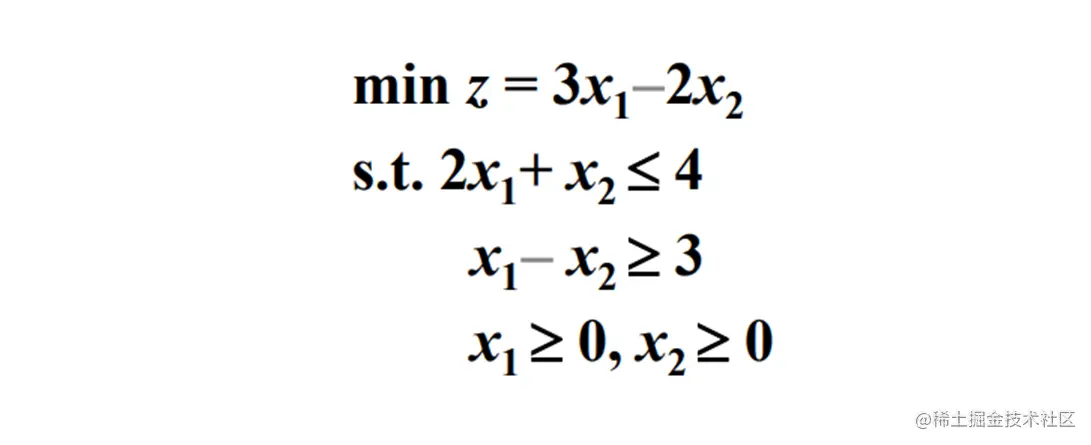
image.png

化为标准形

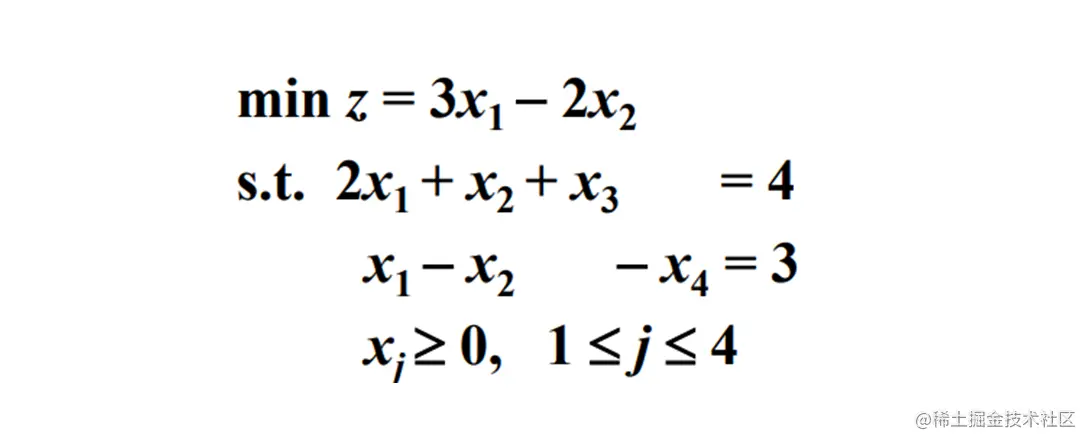
image.png

阶段一辅助函数最优值计算, 引入人工变量 x5x_5

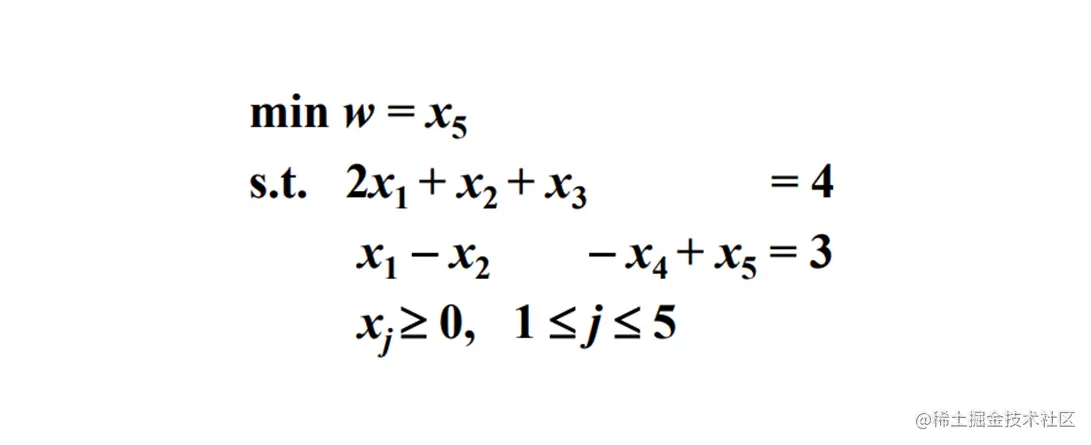
image.png

w∗=1>0w^* = 1 >0 原问题不存在可行解

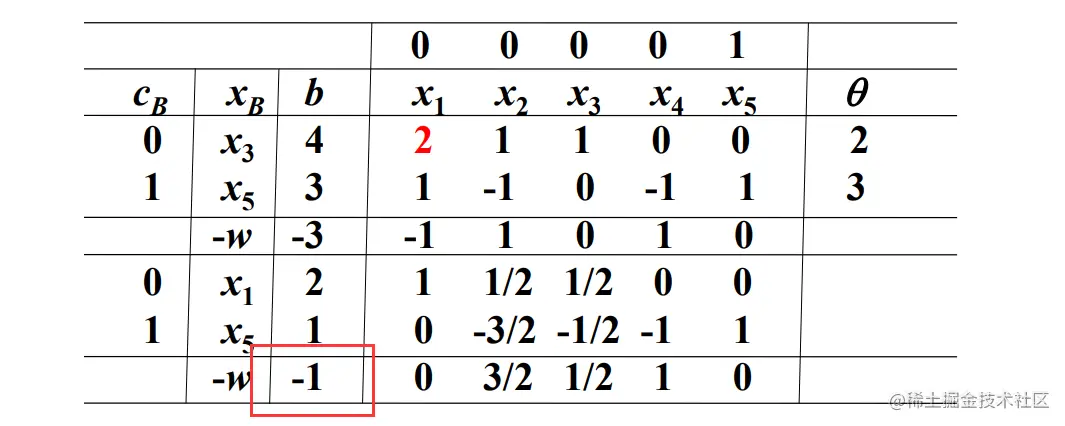
image.png

w*=0 且人工变量为基变量的情况

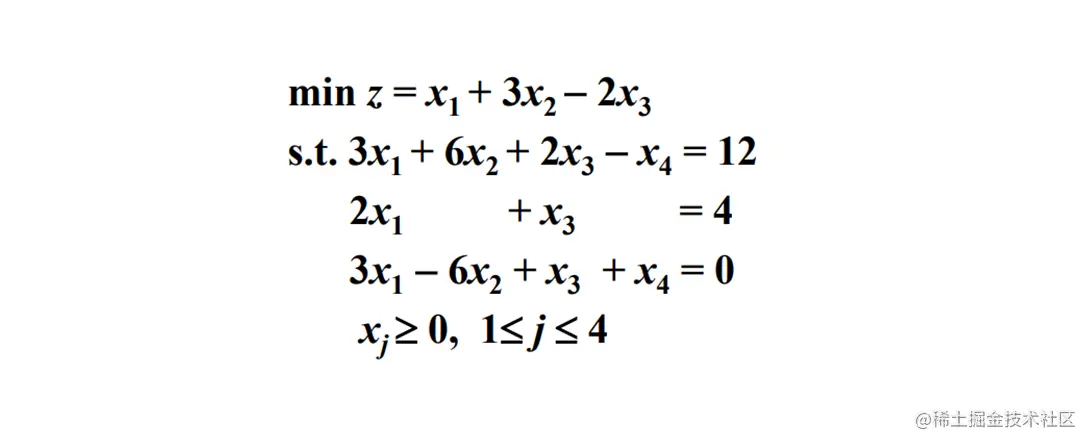
image.png

引入人工变量 x5,x6,x7x_5,x_6,x_7

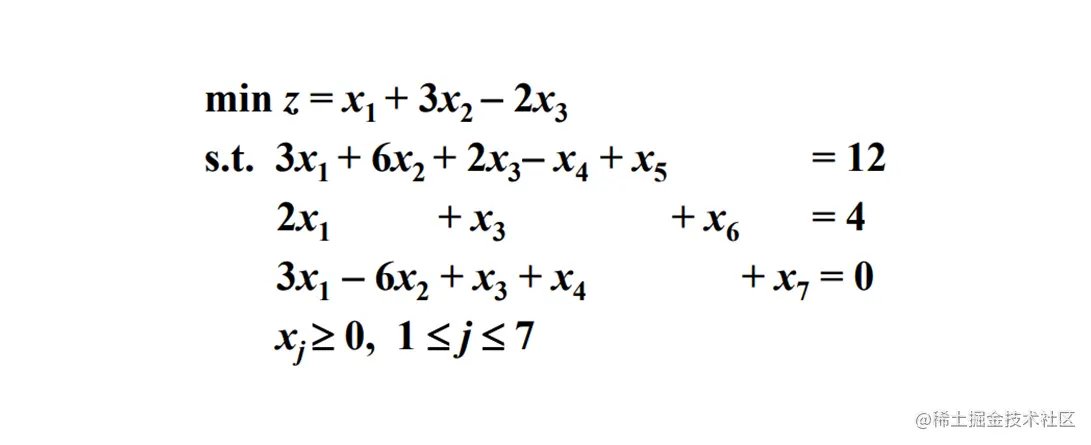
image.png

辅助问题

min w=x5+x6+x7min\ w=x_5+x_6+x_7

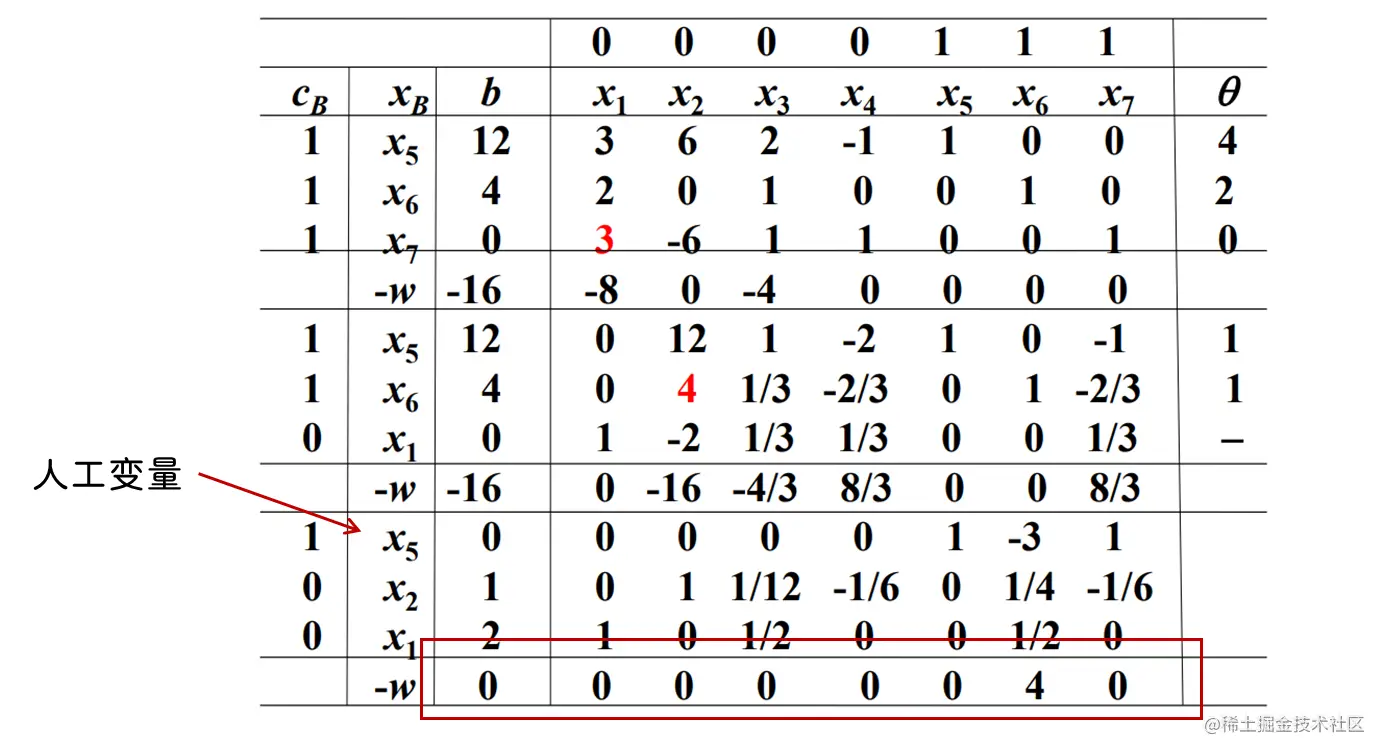
image.png

由于 a11=a12=a13=a14=0a_{11}=a_{12}=a_{13}=a_{14}=0 , β1\beta_1 必为 00 , 因此第一个约束可以由剩下两个约束组合得到, 可以去掉

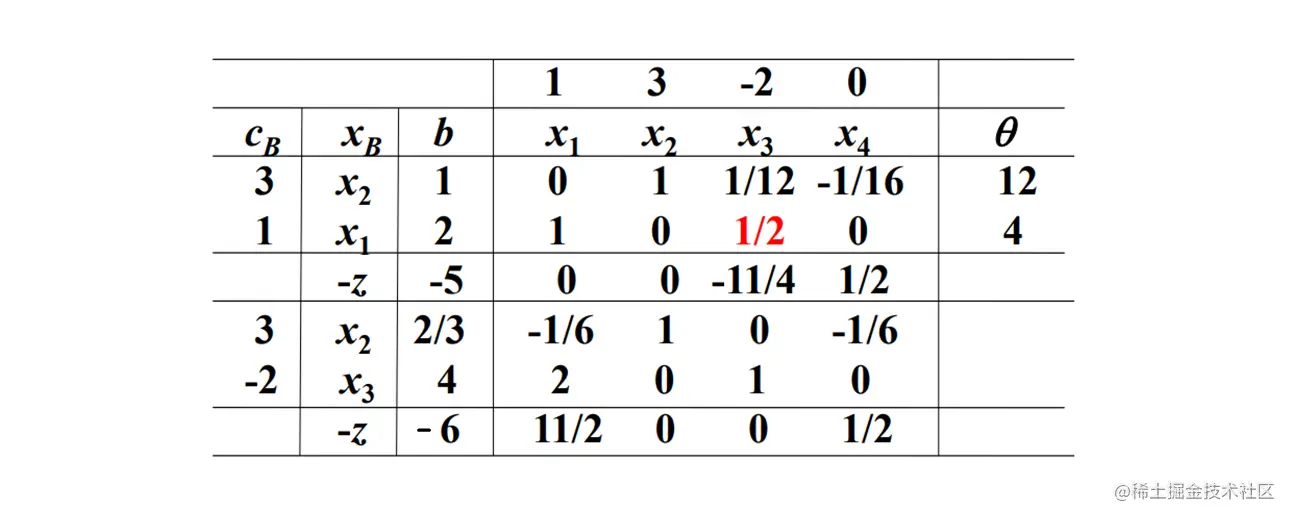
image.png

最优值为 z=6z=6 , 最优解为 x1=0,x2=2/3,x3=4x_1=0, x_2=2/3, x_3=4

有限终止

基本可行解中基变量的值都大于 00 , 则称这个基本可行解是 非退化的

如果线性规划的 所有 基本可行解都是非退化的, 则称这个线性规划是非退化的

如果线性规划有可行解并且是非退化的, 则在计算中可行基不会重复出现, 单纯形法会在有限步内 终止 , 反之计算出现循环

Bland 规则 ( 避免循环 )

  • 当有多个 λj<0\lambda_j < 0 时, 取对应的非基变量中 下标最小 的作为换入变量

  • 当有多个 θi\theta_i 同时取到最小值时, 取对应的基变量中 下标最小 的作为换出变量

avatar
文章
阅读
粉丝