SLAM 技术基础知识汇总—摄像机几何(内参)

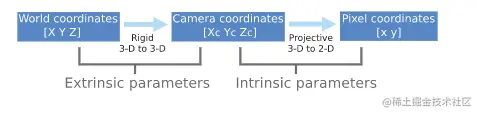
对于从物体如何从 3D 空间投影到 2D 成像平面的过程原理进行适当解释.从针孔摄像机成像原理谈起，涉及到从摄像机坐标系到成像平面的投影矩阵(摄像机内参)，从世界坐标系转换到摄像机坐标系的投影矩阵(外参)。

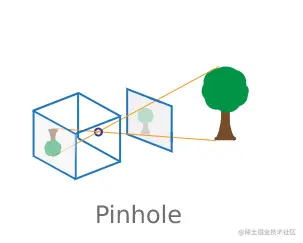
今天相机对于大家来说应该再熟悉不过了，特别是在智能手机出现之后，智能手机的拍照功能让我们每天都能记录生活、工作。不过大家可能还不了解摄像机的成像原理吧，是如何将 3D 世界映射到 2D 平面上的。

随着近几年自动驾驶和 AR 等技术的不断发展，也引起了大家对摄影几何的再次重视，像 3 维重建重这样的技术也成大家关注的焦点的技术。

我们先从实际成像原理来简单介绍一下摄像机模型，接下来进一步基于这个摄像机模型，利用摄像机几何来定义摄像机模型，也就是用数学模型来描述一下摄像机，也就是用数学的语言来描述 3D 空间的点到 2D 成像平面之间的关系。

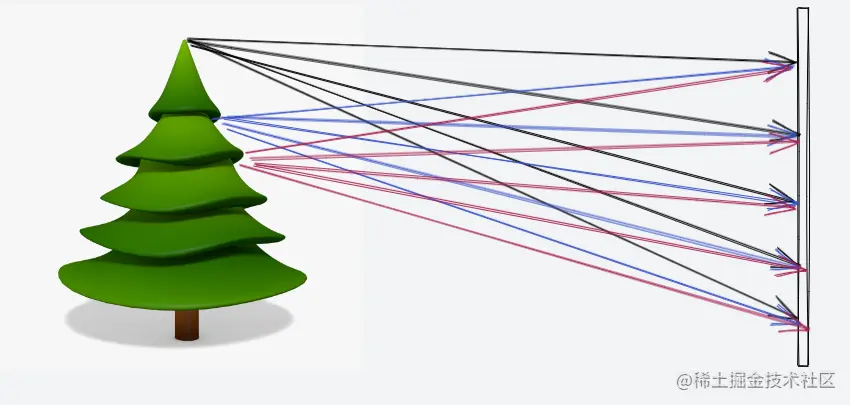
如果我们只是简单将目标物体放置在胶片这样的感光材料前，那么是无法获取清晰图像的。这是因为胶片上每一个点(位置)都能接受到目标上各个位置投射来的光线，这样一来胶片是无法成像的。我们需要找到一种方式让目标物体上的点和胶片上的点是一一对应的，只有这样我们才能够在胶片上看到清晰图像。

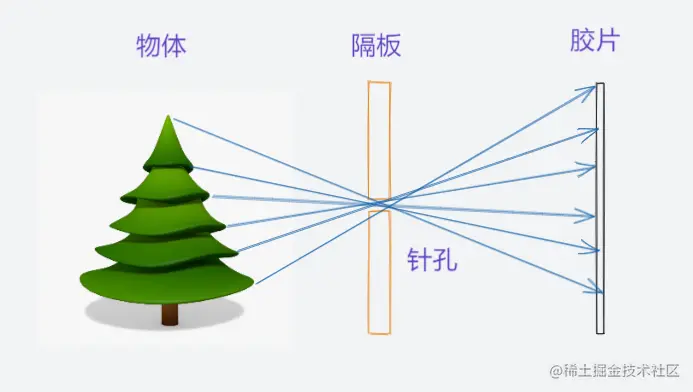
可以在物体和成像胶片之间放置一个带有小孔的隔板，这样就确保了每一条从物体发射光线都是定向，也就是物体上的点与胶片上的点是一一对应的，从而就可以得到一张清晰的图像。

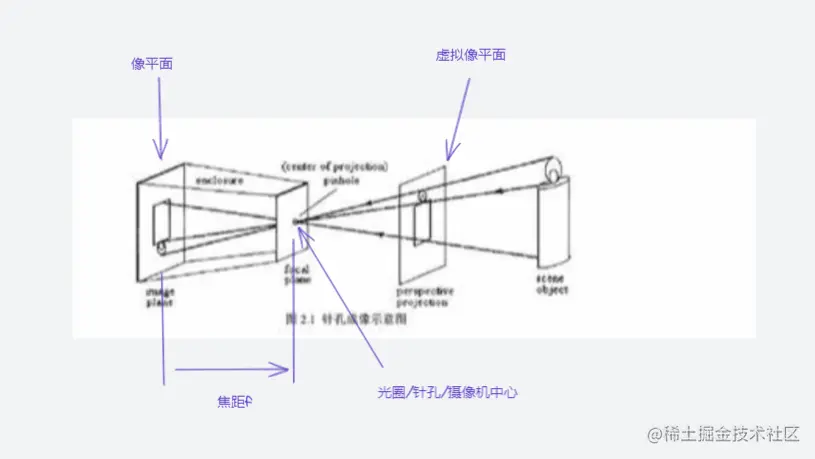
从小孔相机结构图来看，对图中出现的一些概念给予解释，其中这里对于针孔相机来说，有两个比较重要的两个概念，光圈和焦距

光圈: 所谓光圈就是摄像机的小孔，也是摄像机的中心。光圈大小决定了进光的量，如果光圈过大也可能造成图像模糊，当成像过暗时，可以适当地调大光圈来允许更多光进入。不过当光圈放大就可能造成成像模糊
焦距: 焦距是像平面到针孔之间的距离还有一些其他概念
虚拟像平面: 因为像平面上物体是倒置的，并不便于研究，所以在物体一侧假设出一个虚拟像平面，在虚拟像平面上物体方向和真实物体方向一致，而且虚拟像平面到针孔的距离等于焦距。

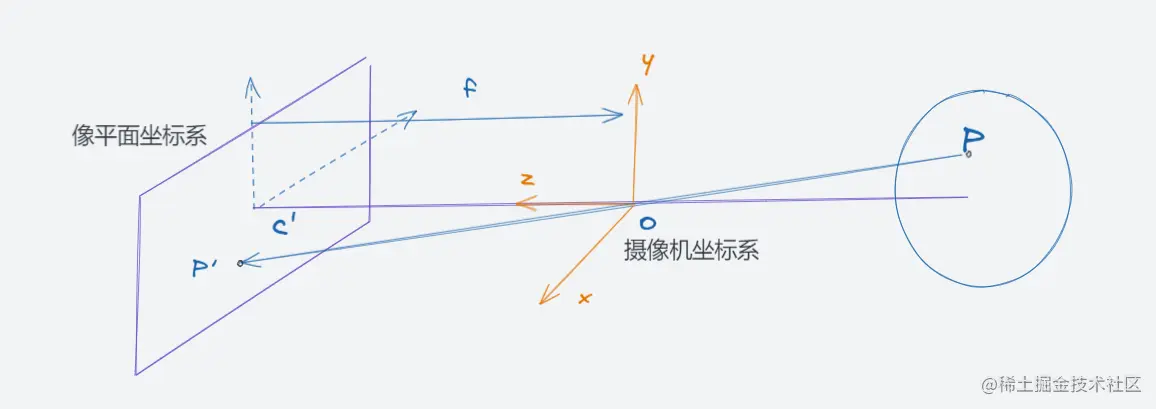
在图上主要有两个坐标系，分别是 3D 空间的摄像机坐标系和 2D 平面的像平面坐标系，这里小孔(光圈)位置就是摄像机坐标系的中心的位置。所谓成像过程，就是将物体上的 P 点映射到像平面上的 $P^{\prime}$ 点的过程

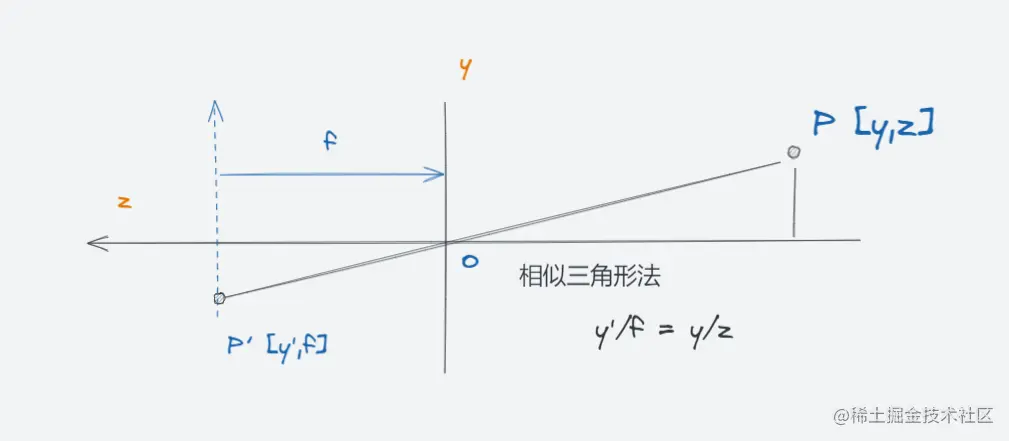
在上图中的平面为 y z o 所组成的平面，在这个平面可以利用三角形相似法来建立如下等式，其中国内 $f$ 为焦距

\frac{y^{\prime}}{f} = \frac{y}{z}

我们用 x, y 和 z 来表示在 3 维空间的一点 P 到像平面上一点 $P^{\prime}$ 可以利用相似三角形来建立关系，如上图。

P = \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} \rightarrow P^{\prime} = \begin{bmatrix} x^{\prime}\\ y^{\prime}\\ \end{bmatrix}

x^{\prime} = f\frac{x}{z} \; y^{\prime} = f\frac{y}{z}

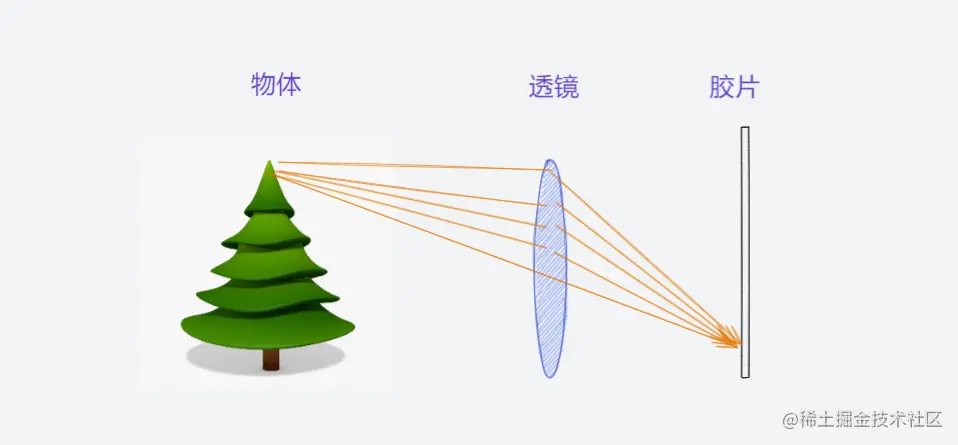
为了解决光线不足问题，可以借助透镜来更多光线投射同一个点

透镜的性质

所有平行光平行于光轴都会会聚到焦点，焦点到透镜中心的距离称为焦距
穿过中心的光线的方向不会发生改变

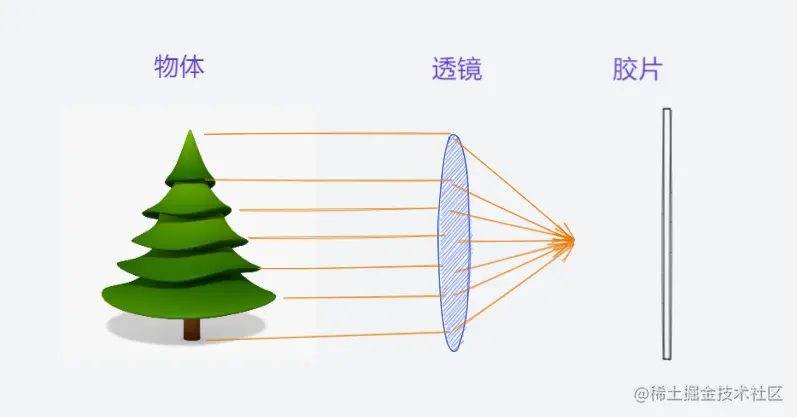
这里平行光会聚的点为焦距(focal point) 和之前中心点到像平面点的焦距并不是一个概念。之前叫做摄像机的焦距，这个焦点叫做透镜的焦距，这两并不是一个概念，需要注意一下。

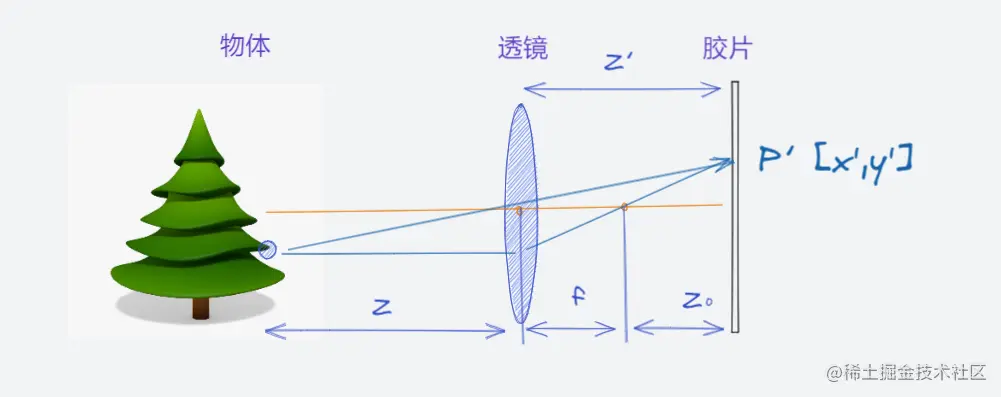
这里不难看出 $Z^{\prime}$ 才是之前说的摄像机焦距，而 $f$ 是透镜焦距那么

z^{\prime} = f + z_0

x^{\prime} = z^{\prime}\frac{x}{z} \; y^{\prime} = z^{\prime}\frac{y}{z}

接下来我们提到焦距，如果没有特殊说明都是指的是摄像机的焦距，而不是透镜的焦距

景深

关于景深这里简单地说一句，就是在景深允许范围内，目标是可以清晰成像的，超出了景深的范围

畸变

径向畸变: 图像像素点以畸变中心为中心点，沿着径向产生的位置偏差，从而导致图像中所成的像发生形变。

枕形畸变
桶形畸变

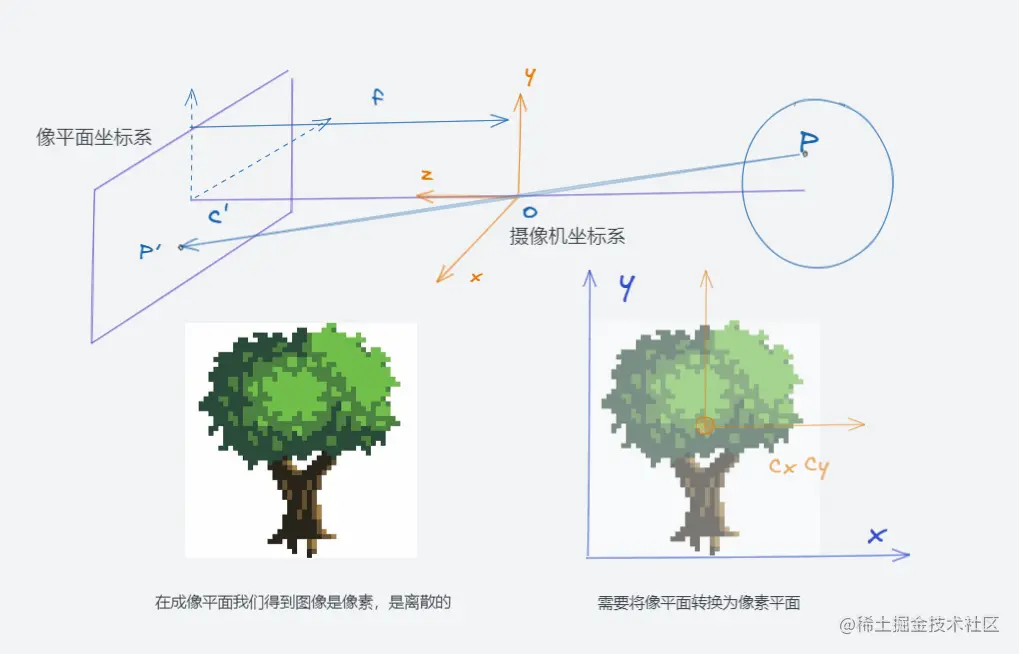
这里还是要提及一下，像平面就是一个中间过程的产物，我们实际成像的平面是像素平面，像素平面是离散的。对于一个 3 维空间点 $P$ 其坐标为 $(x,y,z)$

x^{\prime} = f\frac{x}{z} \; y^{\prime} = f\frac{y}{z}

从像平面到像素平面需要做一些变换

偏置
单位变换

偏置

那么这里 $x^{\prime}$ 在像素平面内点就应该是

x^{\prime} = f\frac{x}{z} + c_x \; y^{\prime} = f\frac{y}{z} + c_y

这是因为像素平面的中心点和像平面的中心点不同，因为要对计算位置进行偏移

单位变换

因为在像平面内单位为 m 而在像素平面内单位为 pixel 所以需要进行单位变换，也就是乘以 pixel/m 将像平面的米制单位转换为像素单位，因为在 x 和 y 轴方向像素

x^{\prime} = f k \frac{x}{z} + c_x \; y^{\prime} = f l \frac{y}{z} + c_y

当一个相机模型确定后 $fk$ 和 $fl$ 这两个参数也就确定了，因为这些都是由相机内部决定的。所以可以将其合并为一个参数 $\alpha$ 和 $\beta$

也就是 $\alpha = fk$ 和 $\beta = fl$

x^{\prime} = \alpha \frac{x}{z} + c_x \; y^{\prime} = \beta \frac{y}{z} + c_y

接下来我们来看从 3 维空间映射到 2 维平面，也就是 $P(x,y,z)$ 映射到 $P^{\prime}(x^{\prime},y^{\prime})$ ,并不是线性关系，因为 $x$ 改变时候会带动 $z$ 的改变，这样 $\frac{\alpha}{z}$ 和 $\frac{\beta}{y}$ 并不是一个常数，所以 $x$ 与 $x^{\prime}$ 并不满足线性关系。

那么如何通过技巧来构造一个线性关系呢?

欧式坐标和齐次坐标的转换

从欧式坐标转换为齐次坐标

(x,y) \rightarrow \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} \; (x,y,z) \rightarrow \begin{bmatrix} x\\ y\\ z \\ 1 \end{bmatrix}

上边分别是图像点的齐次坐标和空间点的齐次坐标。

不难看出从图像点齐次坐标，就是在原有坐标加上一个维度，这样一来就是从空间坐标转换为齐次坐标。这里所以没有用等号，这是因为他们并不是绝对相等，而是相差了一个系数。这个问题在随后从图像反推 3D 空间信息的时候大家就会更加清楚。

从欧式坐标转换为齐次坐标

\begin{bmatrix} x\\ y\\ w \end{bmatrix} \rightarrow (x/w,y/w) \; \begin{bmatrix} x\\ y\\ z \\ w \end{bmatrix} \rightarrow (x/w,y/w,z/w)

对于 3 维空间点齐次坐标除以最后一个维度后得到 2 维空间的点。

齐次坐标系中的投影变换

P_h^{\prime} = \begin{bmatrix} \alpha x + c_x z\\ \beta y + c_y z\\ z\\ \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0\\ 0 & \beta & c_y & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

P_h^{\prime} \rightarrow P^{\prime} = \left( \alpha \frac{x}{z} + c_x, \beta \frac{y}{z} + c_y \right)

这样一来利用齐次坐标把 2 维空间的点和 2 维平面上的点建立一个线性关系。

P^{\prime} = MP

这里还是要声明一下，也就是随后没有特殊说明，所有坐标采用都是齐次坐标表示法，因此不再使用 h 坐标下标来和欧式坐标加以区别。

摄像机偏斜

这里还是值得提一下，就是由于摄像机制作工艺，在像素平面中 x 和 y 夹角可能不是垂直，而是呈现一个 theta 角，也就存在一定偏斜，

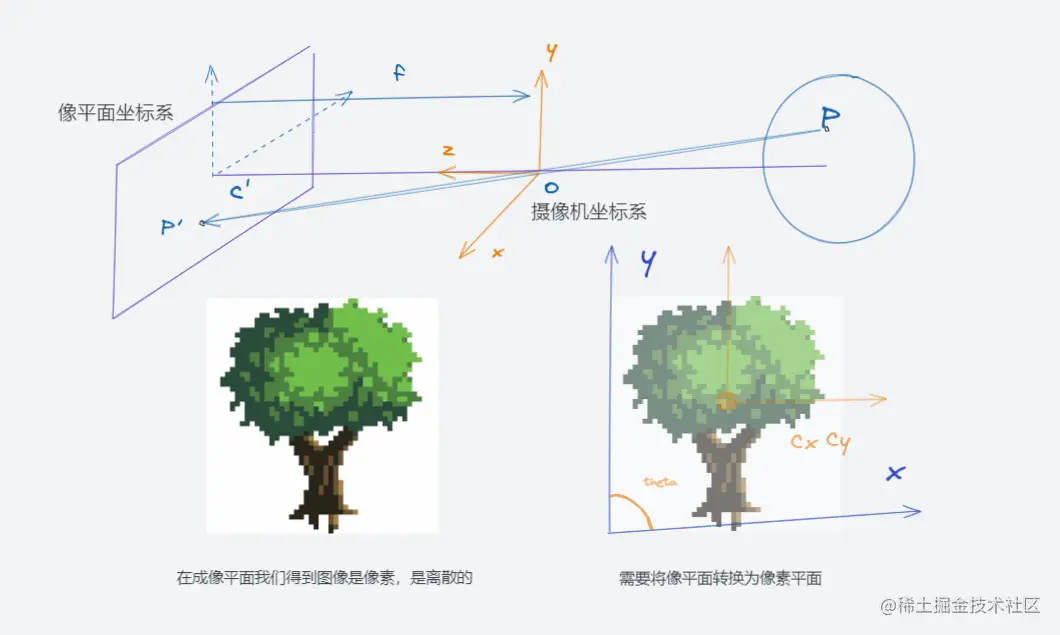
这里建模方式从特殊也就是 x 和 y 夹角为 90 度情况推向一般为 theta

P^{\prime} = \begin{bmatrix} \alpha & -\alpha cot \theta & c_x & 0\\ 0 & \beta/\sin \theta & c_y & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

摄像机内参数

P^{\prime}= MP\\ P^{\prime} = K\begin{bmatrix} I & 0 \end{bmatrix} P

这里 $M$ 是投影矩阵

K = \begin{bmatrix} \alpha & -\alpha cot \theta & c_x \\ 0 & \beta/\sin \theta & c_y \\ 0 & 0 & 1\\ \end{bmatrix}

这里的 $K$ 就是摄像机的内参，内参矩阵主要是将摄像机坐标系下的点映射到像素平面上。

K 有多少个自由度 5 个自由度分别是 $\alpha,\beta,\theta,c_x$ 和 $c_y$ 这 5 个自由度。

规范化摄像机

P^{\prime} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

对于规范化相机，知道我们知道了 2 维点齐次坐标，因为在规范化摄像机，二维点齐次坐标就是 3 维点的坐标。