一、概述

对于无向图模型，我们可以回忆一下它的基于最大团的因子分解（Hammersley–Clifford theorem）。给定概率无向图模型，$C_i,i=1,2,\cdots ,k$为无向图模型上的最大团，则$x$的联合概率分布$P(x)$可以写为：

$$P(x)=\frac{1}{Z}\prod_{i=1}^{k}\psi (x_{C_{i}})\\ C_{i}：最大团\\ x_{C_{i}}：最大团随机变量集合\\ \psi (x_{C_{i}})：势函数，必须为正\\ Z=\sum _{x}\prod_{i=1}^{k}\psi (x_{C_{i}})=\sum _{x_{1}}\sum _{x_{2}}\cdots \sum _{x_{p}}\prod_{i=1}^{k}\psi (x_{C_{i}})$$

对于势函数（Potential Function），通常使用$\psi (x_{C_{i}})=exp\left \{-E(x_{C_{i}})\right \}$，这里的$E$叫做能量函数（Energy Function)，当使用这个势函数时，就有：

$$P(x)=\frac{1}{Z}\prod_{i=1}^{k}\psi (x_{C_{i}})=\frac{1}{Z}exp\left \{-\sum_{i=1}^{k}E(x_{C_{i}})\right \}=\frac{1}{Z}exp\left \{-E(x)\right \}$$

这个分布就叫做吉布斯分布（Gibbs Distribution），或者玻尔兹曼分布（Boltzmann Distribution）。

对于$P(x)=\frac{1}{Z}exp\left \{-\sum_{i=1}^{k}E(x_{C_{i}})\right \}$的形式，可以看出这是一个指数族分布。

对于玻尔兹曼分布$P(x)=\frac{1}{Z}exp\left \{-E(x)\right \}$，这个概念最初来自统计物理学，一个物理系统中存在各种各样的粒子，而$E$代表系统的能量，一个物理系统有多种不同的状态，状态的概率为：

$$P(state)\propto exp\left \{-\frac{E}{k\cdot T}\right \}$$

其中$k$是玻尔兹曼常数（总之就是个常数），$T$是系统温度，可以看出$P(state)$和能量函数成反比，也就是说系统的能量越大，对应的状态的概率越小，系统越不容易停留在这个状态而倾向于向低能量的稳定状态转移。

参考链接：概率图模型

二、表示

玻尔兹曼机（Boltzmann Machine，BM）是一种存在隐节点的无向图模型，它的每个节点对应一个随机变量，分为观测变量和隐变量两种。下图中的概率图就表示了一个玻尔兹曼机，其中阴影部分对应观测变量：

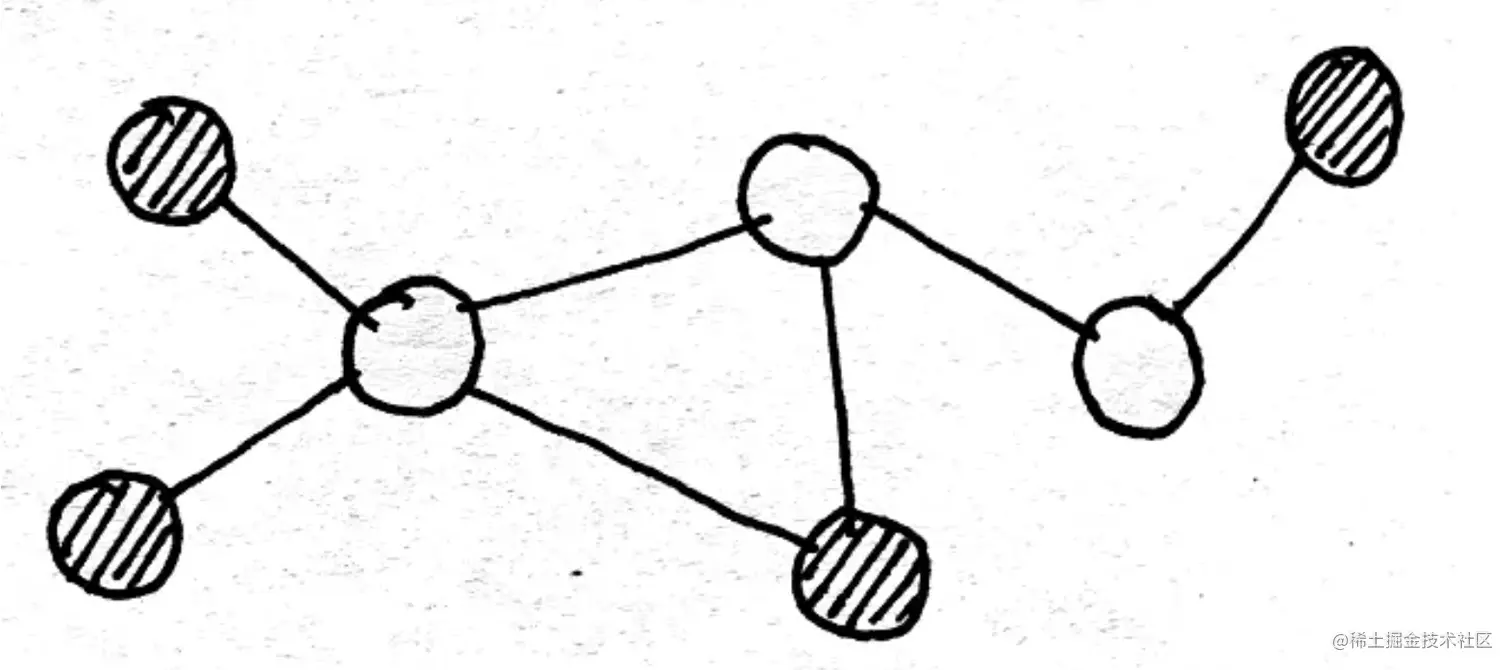
一个玻尔兹曼机的随机变量我们用向量$x$来表示，$x$中包含隐变量和观测变量，隐变量用$h$表示，观测变量用$v$表示，具体的：

$$x=\begin{pmatrix} x_{1}\\ x_{2}\\ \vdots \\ x_{p} \end{pmatrix}=\begin{pmatrix} h\\ v \end{pmatrix}\; \; h=\begin{pmatrix} h_{1}\\ h_{2}\\ \vdots \\ h_{m} \end{pmatrix}\; \; v=\begin{pmatrix} v_{1}\\ v_{2}\\ \vdots \\ v_{n} \end{pmatrix}\; \; p=m+n$$

玻尔兹曼机的问题在于它的推断问题很难解决，其中精确推断的方法是untrackable的，而近似推断的方法计算量太大，因此我们势必需要对模型进行一些简化，也就有了受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）。

在受限玻尔兹曼机中，连接只存在于隐变量与观测变量之间，而隐变量与观测变量内部是无连接的，因此也就得到了一个两层的结构：

受限玻尔兹曼机的概率公式为：

$$P(x)=\frac{1}{Z}exp\left \{-E(x)\right \}$$

也就是：

$$P(v,h)=\frac{1}{Z}exp\left \{-E(v,h)\right \}$$

对于能量函数，在受限玻尔兹曼机中采用以下形式来表示，其中参数是$W,\alpha ,\beta$：

$$E(v,h)=-\left (h^{T}Wv+\alpha ^{T}v+\beta ^{T}h\right )$$

因此概率$P(v,h)$也就可以写成：

$$P(v,h)=\frac{1}{Z}exp\left \{-E(v,h)\right \}\\ =\frac{1}{Z}exp\left \{h^{T}Wv+\alpha ^{T}v+\beta ^{T}h\right \}\\ =\frac{1}{Z}exp\left \{h^{T}Wv\right \}exp\left \{\alpha ^{T}v\right \}exp\left \{\beta ^{T}h\right \}\\ =\frac{1}{Z}\underset{edge}{\underbrace{\prod_{i=1}^{m}\prod_{j=1}^{n}exp\left \{h_{i}w_{ij}v_{j}\right \}}}\underset{node\; v}{\underbrace{\prod_{j=1}^{n}exp\left \{\alpha _{j}v_{j}\right \}}}\underset{node\; h}{\underbrace{\prod_{i=1}^{m}exp\left \{\beta _{i}h_{i}\right \}}}$$

上面这个式子也和受限玻尔兹曼机的因子图一一对应：

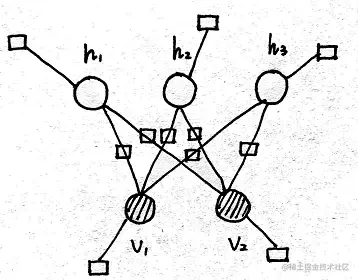
有关因子图的参考链接：概率图模型

受限玻尔兹曼机的参数估计这一篇就不具体介绍了，会在后面配分函数那一篇介绍，下面只推导一下受限玻尔兹曼机的推断问题。

三、推断

1. 后验概率

后验概率包括$P(h|v)$、$P(v|h)$，对于一个无向图，满足局部Markov性质，即：

$$P(h_{l}|h_{-l},v)=P(h_{l}|Neighbour(h_{l}))=P(h_{l}|v)$$

也就是在给定$v$的条件下，$h$的各个分量之间是条件独立的，对于概率$P(h|v)$也就可以改写成：

$$P(h|v)=\sum_{l=1}^{m}P(h_{l}|v)$$

最初的RBM被用来设计解决二值问题，因此这里我们考虑Binary RBM，也就是$h$和$v$的随机变量都是二值的。推断问题是在模型的参数已经得出的前提下进行的，也就是说联合概率$P(v,h)$已经得出，对于后验概率$P(h|v)$的求解，我们希望能够凑出联合概率的形式，考虑概率$P(h_{l}=1|v)$：

$$P(h_{l}=1|v)=P(h_{l}=1|h_{-l},v)\\ =\frac{P(h_{l}=1,h_{-l},v)}{P(h_{-l},v)}\\ =\frac{P(h_{l}=1,h_{-l},v)}{P(h_{l}=1,h_{-l},v)+P(h_{l}=0,h_{-l},v)}$$

对于联合概率$P(v,h)$，在给定$h_l$时，我们可以尝试把$P(v,h)$拆成与$h_l$相关和不相关的两个部分：

$$E(h,v)=-\left (\sum _{i=1}^{m}\sum _{j=1}^{n}h_{i}w_{ij}v_{j}+\sum _{j=1}^{n}\alpha _{j}v_{j}+\sum _{i=1}^{m}\beta _{i}h_{i}\right )\\ =-\left (\underset{\Delta _{1}}{\underbrace{\sum _{i=1,i\neq l}^{m}\sum _{j=1}^{n}h_{i}w_{ij}v_{j}}}+{\color{Red}{\underset{\Delta _{2}}{\underbrace{h_{l}\sum _{j=1}^{n}w_{lj}v_{j}}}}}+\underset{\Delta _{3}}{\underbrace{\sum _{j=1}^{n}\alpha _{j}v_{j}}}+\underset{\Delta _{4}}{\underbrace{\sum _{i=1,i\neq l}^{m}\beta _{i}h_{i}}}+{\color{Red}{\underset{\Delta _{5}}{\underbrace{\beta _{l}h_{l}}}}}\right )$$

最终得到$E(h,v)$的以下形式：

$$\Delta _{2}+\Delta _{5}=h_{l}\left (\sum _{j=1}^{n}w_{lj}v_{j}+\beta _{l}\right )=h_{l}\cdot H_{l}(v)\\ \Delta _{1}+\Delta _{3}+\Delta _{4}=\hat{H}_{l} (h_{-l},v)\\ \therefore E(h,v)=h_{l}\cdot H_{l}(v)+\hat{H}_{l}(h_{-l},v)$$

因此对于$P(h_{l}=1|v)$的分子和分母分别有：

$$分子=\frac{1}{Z}exp\left \{H_{l}(v)+\hat{H}_{l}(h_{-l},v)\right \}\\ 分母=\frac{1}{Z}exp\left \{H_{l}(v)+\hat{H}_{l}(h_{-l},v)\right \}+\frac{1}{Z}exp\left \{\hat{H}_{l}(h_{-l},v)\right \}$$

最终得到概率$P(h_{l}=1|v)$，发现这个概率其实是关于$H_{l}(v)$的sigmoid函数：

$$P(h_{l}=1|v)=\frac{\frac{1}{Z}exp\left \{H_{l}(v)+\hat{H}_{l}(h_{-l},v)\right \}}{\frac{1}{Z}exp\left \{H_{l}(v)+\hat{H}_{l}(h_{-l},v)\right \}+\frac{1}{Z}exp\left \{\hat{H}_{l}(h_{-l},v)\right \}}\\ =\frac{1}{1+exp\left \{\hat{H}_{l}(h_{-l},v)-H_{l}(v)-\hat{H}_{l}(h_{-l},v)\right \}}\\ =\frac{1}{1+exp\left \{-H_{l}(v)\right \}}\\ =\sigma (H_{l}(v))\\ =\sigma (\sum _{j=1}^{n}w_{lj}v_{j}+\beta _{l})$$

类似地也可以得到$P(h_{l}=0|v)$，求得$P(h_{l}|v)$，也就求得了后验概率$P(h|v)$，求解$P(v|h)$的过程与求解$P(h|v)$的过程是完全对称的，这里就不再赘述。

2. 边缘概率

首先将权重矩阵$W$写成行向量的形式，注意这里的$w_i$是行向量：

$$W=[w_{ij}]_{m\times n}=\begin{pmatrix} w_{1}\\ w_{2}\\ \vdots \\ w_{m} \end{pmatrix}$$

为了求解边缘概率$P(v)$，我们只需要将$h$积分掉：

$$P(v)=\sum _{h}P(h,v)\\ =\sum _{h}\frac{1}{Z}exp\left \{-E(v,h)\right \}\\ =\sum _{h}\frac{1}{Z}exp\left \{h^{T}Wv+\alpha ^{T}v+\beta ^{T}h\right \} \\ =\frac{1}{Z}\sum _{h_{1}}\sum _{h_{2}}\cdots \sum _{h_{m}}exp\left \{\underset{与h有关}{\underbrace{h^{T}Wv}}+\underset{与h无关}{\underbrace{\alpha ^{T}v}}+\underset{与h有关}{\underbrace{\beta ^{T}h}}\right \}\\ =\frac{1}{Z}exp\left \{\alpha ^{T}v\right \}\sum _{h_{1}}\sum _{h_{2}}\cdots \sum _{h_{m}}exp\left \{h^{T}Wv+\beta ^{T}h\right \}\\ =\frac{1}{Z}exp\left \{\alpha ^{T}v\right \}\sum _{h_{1}}\sum _{h_{2}}\cdots \sum _{h_{m}}exp\left \{\sum_{i=1}^{m}\left (h_{i}w_{i}v+\beta _{i}h_{i}\right )\right \}\\ =\frac{1}{Z}exp\left \{\alpha ^{T}v\right \}\sum _{h_{1}}\sum _{h_{2}}\cdots \sum _{h_{m}}exp\left \{h_{1}w_{1}v+\beta _{1}h_{1}\right \}exp\left \{h_{2}w_{2}v+\beta _{2}h_{2}\right \}\cdots exp\left \{h_{m}w_{m}v+\beta _{m}h_{m}\right \}\\ =\frac{1}{Z}exp\left \{\alpha ^{T}v\right \}\sum _{h_{1}}exp\left \{h_{1}w_{1}v+\beta _{1}h_{1}\right \}\sum _{h_{2}}exp\left \{h_{2}w_{2}v+\beta _{2}h_{2}\right \}\cdots \sum _{h_{m}}exp\left \{h_{m}w_{m}v+\beta _{m}h_{m}\right \}\\ =\frac{1}{Z}exp\left \{\alpha ^{T}v\right \}\left (1+exp\left \{w_{1}v+\beta _{1}\right \}\right )\left (1+exp\left \{w_{2}v+\beta _{2}\right \}\right )\cdots \left (1+exp\left \{w_{m}v+\beta _{m}\right \}\right )$$

至此这个概率也就求出来了，不过我们还可以进行进一步的变换以发现一些其他的结论：

$$P(v)=\frac{1}{Z}exp\left \{\alpha ^{T}v\right \}\left (1+exp\left \{w_{1}v+\beta _{1}\right \}\right )\left (1+exp\left \{w_{2}v+\beta _{2}\right \}\right )\cdots \left (1+exp\left \{w_{m}v+\beta _{m}\right \}\right )\\ =\frac{1}{Z}exp\left \{\alpha ^{T}v\right \}exp\left \{log\left (1+exp\left \{w_{1}v+\beta _{1}\right \}\right )\right \}exp\left \{log\left (1+exp\left \{w_{2}v+\beta _{2}\right \}\right )\right \}\cdots exp\left \{log\left (1+exp\left \{w_{m}v+\beta _{m}\right \}\right )\right \}\\ =\frac{1}{Z}exp\left \{\alpha ^{T}v+\sum_{i=1}^{m}log\left (1+exp\left \{w_{i}v+\beta _{i}\right \}\right )\right \}$$

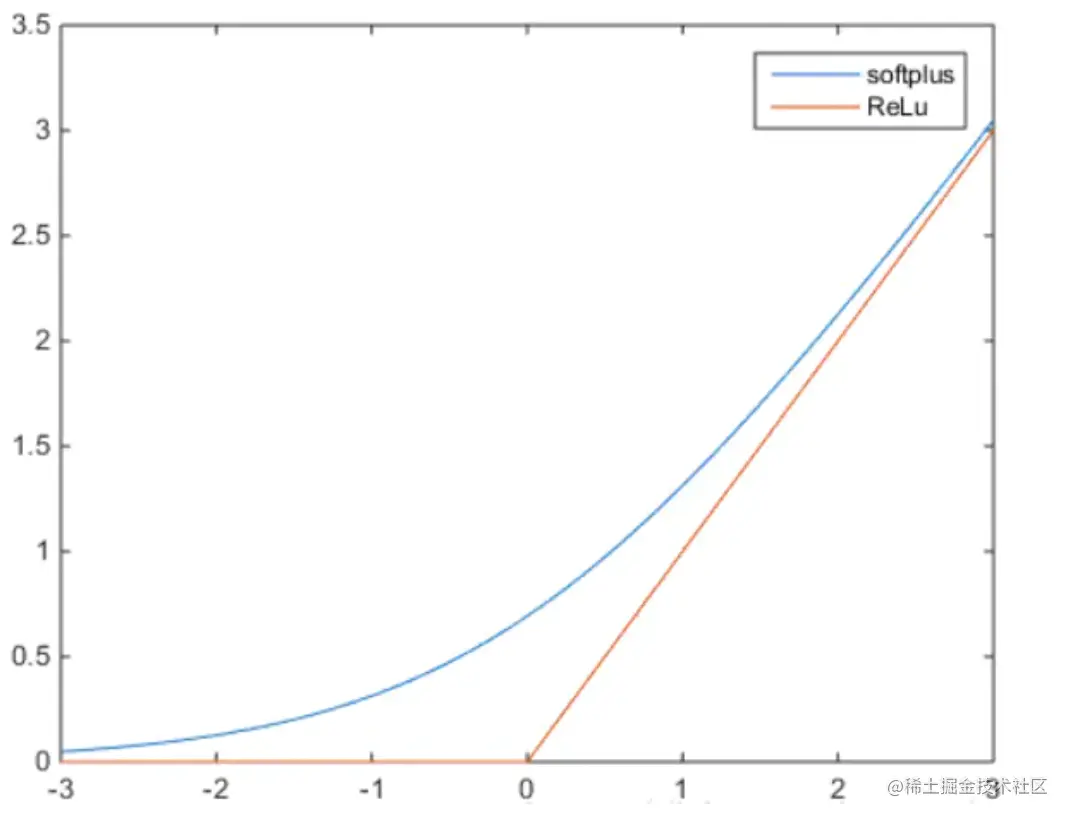
这里的$log(1+e^x)$就是softplus函数，它的图像与Relu函数对比如下：

四、总结

受限玻尔兹曼机是由一个可见层和一个隐藏层组成的双层神经网络。它们之间的节点是全连接的，但同一层的节点之间没有连接。

RBM的学习过程包括两个阶段：训练阶段和抽样阶段。

1. 训练阶段：

   • 初始化可见层和隐藏层的权重矩阵和偏置向量。
   • 对于每个训练样本，通过正向传播计算隐藏层的激活，并通过反向传播更新权重和偏置，使得重构样本与原始样本的误差最小化。
   • 重复上述步骤，直到达到收敛条件。

2. 抽样阶段：

   • 给定一个可见层的样本，通过正向传播计算隐藏层的激活概率。
   • 根据隐藏层的激活状态，通过反向传播计算可见层的重构样本。
   • 重复上述步骤，可以生成新的样本。

RBM的特点和应用：

• RBM是一种无监督学习算法，不需要标注数据进行训练。
• 它可以用于特征学习，通过学习隐含特征的表示，可以在后续任务中提取更有意义的特征。
• RBM也可以用于降维，通过训练一个具有较少隐藏节点的RBM，可以将高维数据映射到低维空间。
• 受限玻尔兹曼机还可以应用于协同过滤任务，如推荐系统，通过学习用户和物品之间的相关性，为用户提供个性化的推荐。

受限玻尔兹曼机也存在一些挑战和限制：

• 训练过程中的收敛速度通常较慢，尤其是在大规模数据和复杂网络结构的情况下。
• 在训练过程中，需要采样和计算概率分布，这可能会导致计算成本较高。
• 受限玻尔兹曼机对于数据的分布假设较为简单，可能无法捕捉到复杂的数据结构和高阶关系。

总结而言，受限玻尔兹曼机是一种重要的无监督学习模型，用于学习数据的概率分布和隐含特征的表示。它在特征学习、降维和协同过滤等任务中发挥重要作用。

此模型之后提出了一些改进和扩展的模型，如深度信念网络（Deep Belief Networks，DBN）、变分自编码器（Variational Autoencoders，VAE）和生成对抗网络（Generative Adversarial Networks，GAN）。这些模型在受限玻尔兹曼机的基础上进行了扩展，提供了更强大和灵活的建模能力。