图形机器学习简介在这篇博文中，我们介绍了图机器学习的基础知识。我们首先研究了什么是图，为什么使用图，以及如何最好地表示

在这篇博文中，我们介绍了图机器学习的基础知识。

我们首先研究了什么是图，为什么使用图，以及如何最好地表示它们。然后，我们简要介绍了人们如何在图上学习，从预神经方法（同时探索图的特征）到通常被称为图神经网络。最后，我们将窥探一下图的变形器世界。

图

什么是图？

就其本质而言，图是对由关系连接的项目的描述。

图的例子包括社交网络（Twitter，Mastodon，任何连接论文和作者的引用网络），分子，知识图（如UML图，百科全书，以及任何页面之间有超链接的网站），表达为其句法树的句子，任何3D网格，以及更多因此，说图无处不在并不是夸张的。

一个图（或网络）的项目被称为它的节点（或顶点），它们的连接是它的边（或链接）。例如，在一个社交网络中，节点是用户，边是连接；在一个分子中，节点是原子，边是分子键。

一个具有类型化节点或类型化边的图被称为异质图（例如：引文网络中的项目可以是论文或作者，具有类型化的节点，而XML图中的关系是类型化的边）。它不能仅仅通过其拓扑结构来表示，它需要额外的信息。这篇文章的重点是同质图。
图也可以是有向的（像一个追随者网络，A跟随B并不意味着B跟随A）或无向的（像一个分子，其中原子之间的关系是双向的）。边可以连接不同的节点或一个节点与自身（自边），但不是所有节点都需要连接。

如果你想使用你的数据，你必须首先考虑其最佳特征（同质/异质，有向/无向，等等）。

图是用来做什么的？

让我们看一下我们可以在图上做的可能任务的小组。

在图的层面上，主要的任务是：

图的生成，用于药物发现以生成新的合理分子、
图的演变（给定一个图，预测它将如何随时间演变），用于物理学预测系统的演变
图层面的预测（从图中进行分类或回归任务），如预测分子的毒性。

在节点层面，通常是节点属性预测。例如，Alphafold使用节点属性预测来预测给定分子总体图的原子的三维坐标，从而预测分子如何在三维空间中得到折叠，这是一个艰难的生物化学问题。

在边缘层面，要么是边缘属性预测，要么是缺失边缘预测。边缘属性预测有助于药物副作用预测，预测给定一对药物的不良副作用。缺失边缘预测用于推荐系统，预测图中的两个节点是否相关。

也可以在子图层面上进行社区检测或子图属性预测。社会网络使用社区检测来确定人们是如何联系的。子图属性预测可以在行程系统（如谷歌地图）中找到，以预测估计的到达时间。

从事这些任务可以通过两种方式进行。

当你想预测一个特定的图的演变时，你在一个过渡性的环境中工作，其中所有的事情（训练、验证和测试）都是在同一个单一的图上完成的。*如果这是你的设置，那就要小心了从一个单一的图中创建训练/验证/测试数据集并非易事。*然而，很多工作是使用不同的图（单独的训练/验证/测试分割）完成的，这被称为归纳设置。

我们如何表示图？

为了处理和操作一个图，常见的表示方法有两种：

作为其所有边的集合（可能辅以其所有节点的集合）。
或作为其所有节点之间的邻接矩阵。邻接矩阵是一个正方形矩阵（节点大小*节点大小），表示哪些节点与其他节点直接相连（其中（A_{ij}=1）如果（n_i）和（n_j）相连，否则为0）。注意：大多数图都不是密集连接的，因此有稀疏的邻接矩阵，这可能会增加计算的难度。

然而，尽管这些表示方法看起来很熟悉，但不要被愚弄了！图与典型的对象有很大不同！

图与ML中使用的典型对象有很大不同，因为它们的拓扑结构比仅仅是 "一个序列"（如文本和音频）或 "一个有序的网格"（例如图像和视频）更复杂）：即使它们可以被表示为列表或矩阵，它们的表示也不应被视为一个有序的对象

但这是什么意思呢？如果你有一个句子，并把它的单词洗牌，你就创造了一个新的句子。如果你有一个图像，并重新排列它的列，你就创造了一个新的图像。

左边是 "拥抱脸 "的标志，右边是洗牌后的 "拥抱脸 "标志，这是一个完全不同的新图像。

图不是这样的：如果你洗了它的边缘列表或它的邻接矩阵的列，它仍然是同一个图。(我们在下面一点的地方更正式地解释这个问题，请看包络不变性）。

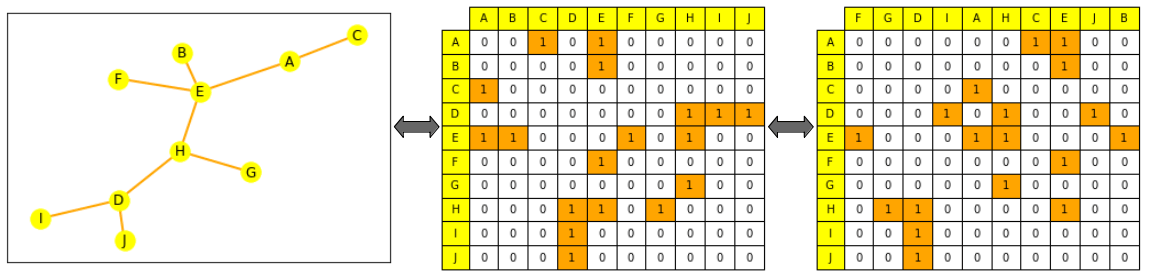
左边是一个小图（节点为黄色，边为橙色）。中间是它的邻接矩阵，列和行都是按字母顺序排列的：在节点A的那一行（第一行），我们可以读出它与E和C相连：A仍然与E和C相连。

通过ML进行图的表示

用机器学习处理图的通常过程是，首先为你感兴趣的项目生成一个有意义的表示（节点、边或完整的图，取决于你的任务），然后用这些表示为你的目标任务训练一个预测器。我们希望（就像在其他模式中一样）约束你的对象的数学表征，使类似的对象在数学上接近。然而，这种相似性在图ML中很难严格定义：例如，当两个节点有相同的标签或相同的邻居时，它们是否更相似？

注意：在下面的章节中，我们将专注于生成节点的表示。一旦你有了节点级的表示，就有可能获得边或图级的信息。对于边级信息，你可以将节点对的表示连接起来，或者做点乘。对于图级信息，可以对所有节点级表征的串联张量做一个全局集合（平均、总和等）。但是，它仍然会使整个图的信息变得平滑和丢失 -- 递归的分层集合可能更有意义，或者增加一个虚拟节点，与图中所有其他节点相连，并将其表示作为整个图的表示。

前神经方法

简单地使用工程化的特征

在神经网络之前，图和其感兴趣的项目可以被表示为特征的组合，以特定的任务方式。现在，这些特征仍然被用于数据增强和半监督学习，尽管存在更复杂的特征生成方法；根据你的任务，找到如何最好地提供给你的网络可能是至关重要的。

节点级特征可以提供关于重要性的信息（这个节点对图的重要性如何？）和/或基于结构的信息（节点周围的图的形状是什么？），并且可以结合起来。

节点中心性衡量节点在图中的重要性。它可以通过递归计算每个节点的邻居的中心度之和直到收敛，或者通过节点之间的最短距离测量，例如。节点度是指它拥有的直接邻居的数量。聚类系数衡量节点邻居的连接程度。小图程度向量计算有多少不同的小图根植于给定的节点，其中小图是你可以用给定数量的连接节点创建的所有小图（有三个连接节点，你可以有一条有两条边的线，或一个有三条边的三角形）。

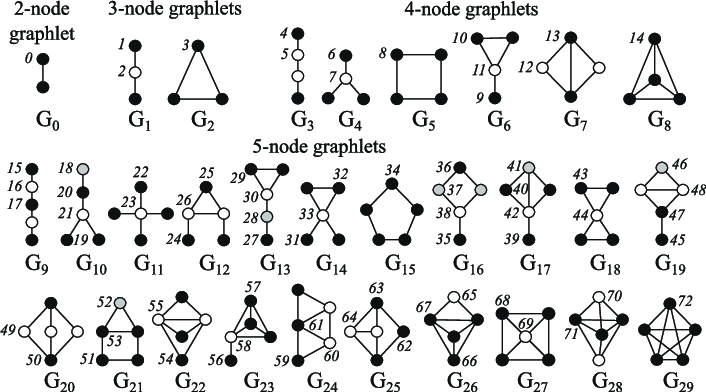
2-5个节点的小图（Pržulj, 2007）

边缘级特征用关于节点连接性的更详细的信息来补充表示，包括两个节点之间的最短距离，它们的共同邻居，以及它们的Katz指数（这是两个节点之间可能走到一定长度的数量--它可以直接从邻接矩阵计算出来）。

图层面的特征包含关于图相似性和特殊性的高级信息。总的小图计数，尽管计算成本很高，但提供了关于子图形状的信息。核心方法通过不同的 "节点袋 "方法（类似于词袋）来测量图之间的相似性。

基于步行的方法

基于行走的方法使用随机行走中从节点i访问节点j的概率来定义相似性度量；这些方法结合了局部和全局信息。 Node2Vec例如，模拟图中节点之间的随机行走，然后用跳格处理这些行走，就像我们处理句子中的单词一样，来计算嵌入。这些方法也可以用来加速计算 网页排名方法的计算，该方法为每个节点分配一个重要性分数（基于它与其他节点的连接性，例如，通过随机行走评估其访问频率）。

然而，这些方法有局限性：它们不能获得新节点的嵌入，不能很好地捕捉节点之间的结构相似性，也不能使用添加的特征。

图谱神经网络

神经网络可以泛化到未见过的数据。考虑到我们前面提到的表征限制，一个好的神经网络应该是什么，才能在图上工作？

它应该：

具有包络不变性：
- 公式：f(P(G ) )=f(G)f(P(G))=f(G)，f是网络，P是包络函数，G是图形。
- 解释：通过网络后，图的表示和它的互换应该是相同的。
是互换等值的
- 方程：P(f(G ))=f(P (G ) )P(f(G))=f(P(G))，f是网络，P是置换函数，G是图形。
- 解释：在将节点传递给网络之前对其进行置换，应该等同于对其表示进行置换。

典型的神经网络，如RNNs或CNNs都不具有包络不变性。因此，一种新的架构，即图谱神经网络，被引入（最初是基于状态的机器）。

一个GNN是由连续的层组成的。一个GNN层表示一个节点是它的邻居和它自己的表示的组合**（聚合**），来自上一层**（消息传递**），加上通常的激活以增加一些非线性。

与其他模型的比较：一个CNN可以被看作是一个具有固定邻居大小（通过滑动窗口）和排序（它不是包换等价的）的GNN。一个没有位置嵌入的转化器可以被看作是一个全连接输入图上的GNN。

聚合和消息传递

有很多方法可以聚合来自邻居节点的消息，例如求和、求平均。一些遵循这一理念的著名作品包括：

图卷积网络对一个节点的邻居的归一化表示进行平均（大多数GNN实际上是GCN）；
图注意网络学会根据不同邻居的重要性来衡量它们（像变压器）；
GraphSAGE对不同跳数的邻居进行采样，然后用最大池的方式分几步汇总它们的信息。
图形同构网络通过对邻居的节点表征之和应用MLP来聚合表征。

选择一个聚合：一些聚合技术（特别是平均/最大集合）在创建表征时可能会遇到失败的情况，这些表征可以精细地区分类似节点的不同邻居（例如：通过平均集合，一个有4个节点的邻居，表示为1,1,-1,-1，平均为0，与一个只有3个节点表示为-1,0,1的邻居不会有区别）。

GNN形状和过度平滑问题

在每一个新的层，节点表示包括越来越多的节点。

一个节点，通过第一层，是其直接邻居的聚合。通过第二层，它仍然是其直接邻居的聚合，但这一次，他们的表示包括他们自己的邻居（来自第一层）。经过n层后，所有节点的表示就变成了它们所有距离为n的邻居的集合，因此，如果其直径小于n的话，就变成了整个图的集合！

如果你的网络有太多的层，就有可能使每个节点成为全图的聚合（而且所有节点的表示都收敛为同一个）。这就是所谓的过度平滑问题

这可以通过以下方式解决：

缩放GNN，使其层数小到足以不把每个节点近似为整个网络（首先分析图的直径和形状）。
增加各层的复杂性
增加非信息传递层来处理信息（如简单的MLPs）。
增加跳过连接。

过度平滑问题是图ML的一个重要研究领域，因为它阻止了GNN的扩展，就像变形器在其他模式中被证明的那样。

图变换器

没有位置编码层的Transformer是不变的，而且Transformer被认为可以很好地扩展，所以最近，人们开始研究将Transformer适应于图（Survey）。大多数方法的重点是通过寻找最佳特征和最佳方式来表示图形，并改变注意力以适应这种新数据。

下面是一些有趣的方法，它们在截至本文撰写时的最难的可用基准之一--斯坦福大学的Open Graph Benchmark上得到了最先进的结果或接近：

用于图到序列学习的图变换器(Cai和Lam, 2020）介绍了一个图形编码器，它将节点表示为其嵌入和位置嵌入的串联，将节点关系表示为它们之间的最短路径，并将两者结合在一个关系增强的自我关注中。
用频谱注意力重新思考图变换器(Kreuzer等人，2021）引入了光谱注意网络（SAN）。这些结合了节点特征和学习到的位置编码（从拉普拉斯特征向量/值计算），作为注意力中的键和查询，注意力值是边缘特征。
GRPE：图形变换器的相对位置编码(Park等人，2021）介绍了图的相对位置编码转化器。它通过将图层面的位置编码与节点信息相结合，边缘层面的位置编码与节点信息相结合，并将两者结合在注意力中来表示一个图。
全局自我注意作为图卷积的替代品(Hussain等人，2021）介绍了边缘增强变换器。这种架构分别嵌入节点和边，并将它们聚集在一个修正的注意力中。
变换器对图的表现真的很差吗？(Ying等人, 2021）介绍了微软的 Graphormer，它一出来就赢得了OGB的第一名。这种架构在注意力中使用节点特征作为查询/键/值，并在注意力机制中用中心性、空间性和边缘编码的组合来总结它们的表现。

最新的方法是 纯粹的变换器是强大的图学习器(Kim等人，2022），它引入了TokenGT。这种方法将输入图表示为节点和边嵌入的序列（用正交节点标识符和可训练的类型标识符增强），没有位置嵌入，并将这个序列作为输入提供给变形器。它非常简单，但也很聪明!

有点不同、 一个通用的、强大的、可扩展的图变换器的配方(Rampášek et al, 2022)介绍的不是一个模型，而是一个框架，叫做GraphGPS。它允许将消息传递网络与线性（长距离）变换器结合起来，轻松创建混合网络。这个框架还包含几个工具来计算位置和结构编码（节点、图、边缘级别）、特征增强、随机行走等。

对图形使用变换器在很大程度上仍然是一个处于起步阶段的领域，但它看起来很有希望，因为它可以减轻GNN的一些限制，例如扩展到更大/更密集的图形，或增加模型大小而不过度平滑。

图形机器学习简介

图