平面上点到直线的距离公式证明

平面上点到直线的距离公式证明

点到直线的距离公式 设直线的方程是

那么点$P_0(x_0,y_0)$到直线$l$的距离是

证明 我们这里利用向量工具来证明：

我们假设直线$l: Ax+By+C=0$的法向量为$\mathbf{n}$（方向朝上或朝下无所谓），点M, N为直线$l$上的任意两点（不重合），点Q为点P到直线$l$的垂线段的垂足，如图：

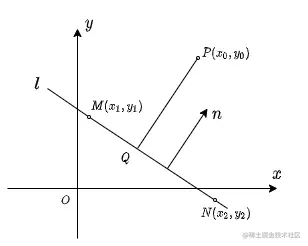
设$M(x_1,y_1)$和$N(x_2,y_2)$，我们可以求得向量$\overrightarrow{MN} = (x_2-x_1, y_2-y_1)$，又由于点M和N在直线$l$上，所以有方程组

成立，我们将两个方程相减，得$A(x_2-x_1)+B(y_2-y_1)=0$，即

这里的$\cdot$代表向量内积。所以向量$(A,B)$与向量$\overrightarrow{MN}$垂直（即与直线$l$垂直）， 所以法向量为$\mathbf{n}$与$(A,B)$平行，这里我们就假设$\mathbf{n} = (A,B)$， 由于PQ垂直于直线$l$，所以向量$\overrightarrow{PQ}$平行于$\mathbf{n}$（同向或反向无所谓），所以$\overrightarrow{PQ} = t(A,B)$，这里$t$为实数，我们设Q的坐标为$(x,y)$，所以$(x-x_0, y-y_0) = t(A,B)$，即

又由点Q在直线$l$上（点Q为点P到直线$l$的垂线段的垂足），所以有

把方程组代入直线方程有：

解出t：

在根据两点间距离公式，有

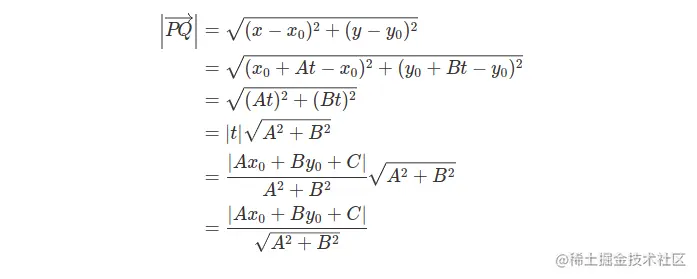
最后的式子就是需要证明的点到直线的距离公式。