一、概述

线性回归的数据如下所示：

$$D=\left \{(x_{1},y_{1}),(x_{2},y_{2}),\cdots ,(x_{N},y_{N})\right \}\\ x_{i}\in \mathbb{R}^{p},y_{i}\in \mathbb{R},i=1,2,\cdots ,N \\ X=(x_{1},x_{1},\cdots ,x_{N})^{T}=\begin{pmatrix} x_{1}^{T}\\ x_{2}^{T}\\ \vdots \\ x_{N}^{T} \end{pmatrix}=\begin{pmatrix} x_{11} & x_{12} & \cdots &x_{1p} \\ x_{21} & x_{22}& \cdots &x_{2p} \\ \vdots & \vdots & \ddots &\vdots \\ x_{N1}& x_{N2} & \cdots & x_{Np} \end{pmatrix}_{N \times p}\\ Y=\begin{pmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{N} \end{pmatrix}_{N \times 1}$$

对于线性回归问题，假设：

$$f(x)=w^{T}x\\ y=f(x)+\varepsilon \\ \varepsilon \sim N(0,\sigma ^{2})$$

其中$w$是参数，$\varepsilon$是噪声。以二维的数据为例，其图像如下：

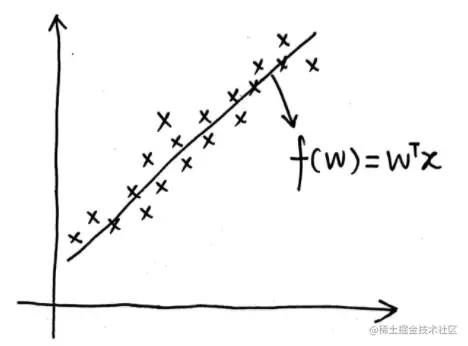
从几何角度出发求解线性回归问题，可以使用最小二乘估计（Least Square Estimate，LSE），而从概率角度来看也就是噪声为高斯分布的极大似然估计（Maximum Likelihood Estimate，MLE），公式为：

$$w_{MLE}=\underset{w}{argmax}\; P(Data|w)$$

为了防止过拟合的问题，采用了正则化的最小二乘估计的方法，包括Lasso正则化和Ridge正则化两种方式，这种方法从概率角度来看也就是最大后验估计（Maximum a Posteriori Estimation，MAP），其噪声也是高斯分布，这里参数$w$的后验满足：

$$P(w|Data)\propto P(Data|w)\cdot P(w)$$

因此最大后验估计的公式也就是：

$$w_{MAP}=\underset{w}{argmax}\; P(w|Data)=\underset{w}{argmax}\; P(Data|w)\cdot {\color{Red}{P(w)}}$$

这里的$P(w)$也就是参数$w$的先验，如果$P(w)$服从高斯分布，则对应Lasso正则化，如果$P(w)$服从拉普拉斯分布，则对应Ridge正则化。

对于上述方法的详细解释，可以参考链接：线性回归 。

上述方法都是点估计方法，而在贝叶斯线性回归中我们希望利用贝叶斯学派的方法来求解出后验概率分布$P(w|Data)$。

二、推断与预测

1.推断

贝叶斯线性回归的推断（Inference）任务也就是求解参数$w$的后验分布$P(w|Data)$。首先，进行以下变换：

$$P(w|Data)=P(w|X,Y)\\ =\frac{P(w,Y|X)}{P(Y|X)}\\ =\frac{{\color{Red}{P(Y|w,X)}}\cdot {\color{Blue}{P(w|X)}}}{\int P(Y|w,X)\cdot P(w|X)\mathrm{d}w}$$

对于上面得到的式子，分子中$P(Y|w,X)$相当于似然，$P(w|X)$也就是先验$P(w)$（因为$w$和$X$没有关系)，另外分母是一个常数，因此我们可以得到：

$$P(w|Data)\propto P(Y|w,X)\cdot P(w)$$

对于似然$P(Y|w,X)$，由于之前定义的$y$和$x$之间的关系是一个线性高斯模型，因此可以得到：

$$P(Y|w,X)=\prod_{i=1}^{N}P(y_{i}|w,x_{i})=\prod_{i=1}^{N}N(y_{i}|w^{T}x_{i},\sigma ^{2})$$

对于先验$P(w)$，是人为指定的，只要合理就可以任意给定这个分布，通常我们选择高斯分布，注意这里是一个多维的高斯分布，我们选择的高斯分布均值为$0$，方差矩阵用$\Sigma _{p}$来表示：

$$P(w)=N(0,\Sigma _{p})$$

因此也就得到：

$$P(w|Data)\propto \prod_{i=1}^{N}N(y_{i}|w^{T}x_{i},\sigma ^{2})\cdot N(0,\Sigma _{p})$$

由于似然$P(Y|w,X)$和先验$P(w)$都是高斯分布，利用共轭的知识（高斯分布是自共轭的），我们也可以得到$P(w|Data)$也是一个高斯分布，推断任务也就是求解这个高斯分布的均值和方差，我们用$\mu _{w}$和$\Sigma _{w}$来表示这个高斯分布的均值和方差：

$$P(w|Data)\sim N(\mu _{w},\Sigma _{w})$$

将似然$P(Y|w,X)$做进一步的变换，我们可以得到这个概率的均值和方差：

$$P(Y|w,X)=\prod_{i=1}^{N}\frac{1}{(2\pi )^{1/2}\sigma }exp\left \{-\frac{1}{2\sigma ^{2}}(y_{i}-w^{T}x_{i})^{2}\right \}\\ =\frac{1}{(2\pi )^{N/2}\sigma ^{N}}exp\left \{-\frac{1}{2\sigma ^{2}}{\color{Red}{\sum _{i=1}^{N}(y_{i}-w^{T}x_{i})^{2}}}\right \}$$

上式中红色的部分可以写成矩阵相乘的形式：

$$\sum _{i=1}^{N}(y_{i}-w^{T}x_{i})^{2}=\underset{Y^{T}-w^{T}X^{T}}{\underbrace{\begin{pmatrix} y_{1}-w^{T}x_{1} & y_{2}-w^{T}x_{2} & \cdots & y_{N}-w^{T}x_{N} \end{pmatrix}}}\begin{pmatrix} y_{1}-w^{T}x_{1}\\ y_{2}-w^{T}x_{2}\\ \vdots \\ y_{N}-w^{T}x_{N} \end{pmatrix}\\ =(Y^{T}-w^{T}X^{T})(Y-Xw)\\ =(Y-Xw)^{T}(Y-Xw)$$

因此也就有：

$$P(Y|w,X)=\frac{1}{(2\pi )^{N/2}\sigma ^{N}}exp\left \{-\frac{1}{2\sigma ^{2}}\sum _{i=1}^{N}(y_{i}-w^{T}x_{i})^{2}\right \}\\ =\frac{1}{(2\pi )^{N/2}\sigma ^{N}}exp\left \{-\frac{1}{2\sigma ^{2}}(Y-Xw)^{T}(Y-Xw)\right \}\\ =\frac{1}{(2\pi )^{N/2}\sigma ^{N}}exp\left \{-\frac{1}{2}(Y-Xw)^{T}\sigma ^{-2}I(Y-Xw)\right \}\\ =N(Xw,\sigma ^{2}I)$$

至此似然$P(Y|w,X)$就表示成了标准的高斯分布的形式，代入后验中我们可以得到：

$$P(w|Data)\propto N(Xw,\sigma ^{2}I)\cdot N(0,\Sigma _{p})\\ \propto exp\left \{-\frac{1}{2}(Y-Xw)^{T}\sigma ^{-2}I(Y-Xw)\right \}\cdot exp\left \{-\frac{1}{2}w^{T}\Sigma _{p}^{-1}w\right \}\\ =exp\left \{-\frac{1}{2\sigma ^{2}}(Y-Xw)^{T}(Y-Xw)-\frac{1}{2}w^{T}\Sigma _{p}^{-1}w\right \}\\ =exp\left \{-\frac{1}{2\sigma ^{2}}(Y^{T}Y-2Y^{T}Xw+w^{T}X^{T}Xw)-\frac{1}{2}w^{T}\Sigma _{p}^{-1}w\right \}$$

对于上面的式子我们可以写出它的指数的关于$w$的二次项和一次项：

$$二次项：-\frac{1}{2\sigma ^{2}}w^{T}X^{T}Xw-\frac{1}{2}w^{T}\Sigma _{p}^{-1}w=-\frac{1}{2}w^{T}(\sigma ^{-2}X^{T}X+\Sigma _{p}^{-1})w\\ 一次项：-\frac{1}{2\sigma ^{2}}(-2Y^{T}Xw)=\sigma ^{-2}Y^{T}Xw$$

对于一个多维的高斯分布的指数部分，将其展开可以得到：

$$exp\left \{-\frac{1}{2}(X-\mu)^{T}\Sigma ^{-1}(X-\mu)\right \}\\ =exp\left \{-\frac{1}{2}(X^{T}\Sigma ^{-1}-\mu^{T}\Sigma ^{-1})(X-\mu)\right \}\\ =exp\left \{-\frac{1}{2}(\underset{二次项}{\underbrace{X^{T}\Sigma ^{-1}X}}\underset{一次项}{\underbrace{-2\mu^{T}\Sigma ^{-1}X}}+\mu^{T}\Sigma ^{-1}\mu)\right \}$$

而这里的有关于$X$的二次项和一次项为：

$$二次项：-\frac{1}{2}X^{T}\Sigma ^{-1}X\\ 一次项：\mu^{T}\Sigma ^{-1}X$$

通过二次项也就可以得到后验$P(w|Data)$的精度矩阵$\Lambda _{w}$（这是一个对称矩阵)：

$$\Lambda _{w}=\Sigma _{w}^{-1}=\sigma ^{-2}X^{T}X+\Sigma _{p}^{-1}$$

由一次项可以得出：

$$\mu _{w}^{T}\Sigma _{w}^{-1}=\mu _{w}^{T}\Lambda _{w}=\sigma ^{-2}Y^{T}X\\ \Rightarrow \Lambda _{w}\mu _{w}=\sigma ^{-2}X^{T}Y\\ \Rightarrow \mu _{w}=\sigma ^{-2}\Lambda _{w}^{-1}X^{T}Y$$

如此我们最终就求得了后验$P(w|Data)$的均值和方差：

$$\mu _{w}=\sigma ^{-2}\Lambda _{w}^{-1}X^{T}Y\\ \Sigma _{w}=\Lambda _{w}^{-1}\\ 其中\Lambda _{w}=\sigma ^{-2}X^{T}X+\Sigma _{p}^{-1}$$

2.预测

预测（Prediction）问题是利用已经求解出来的贝叶斯线性回归模型，在给定$x^{*}$的前提下，求解$y^{*}$。要注意，由于这里的$w$服从后验分布$P(w|Data)$，因此需要求解的是分布$P(y^{*}|Data,x^{*})$。

首先对于$f(x^{*})$，有$f(x^{*})=(x^{*})^{T}w$，而$w$服从后验分布$N(\mu _{w},\Sigma _{w})$，$x^{*}$可以看做一个常数，因此就有：

$$f(x^{*})=(x^{*})^{T}w\sim N((x^{*})^{T}\mu _{w},(x^{*})^{T}\Sigma _{w}x^{*})$$

另外有$y^{*}=f(x^{*})+\varepsilon$，$\varepsilon \sim N(0,\sigma ^{2})$，因此就有（两个高斯分布随机变量相加后的概率分布相当于将两个高斯分布的均值和方差均相加得到的高斯分布)：

$$P(y^{*}|Data,x^{*})=N((x^{*})^{T}\mu _{w},(x^{*})^{T}\Sigma _{w}x^{*}+\sigma ^{2})$$

综合一下，具体的过程为：

$$P(y^{*}|Data,x^{*})=\int _{w}P(y^{*}|w,X,Y,x^{*})P(w|X,Y,x^{*})\mathrm{d}w\\ =\int _{w}P(y^{*}|w,x^{*})P(w|X,Y)\mathrm{d}w\\ =N((x^{*})^{T}\mu _{w},(x^{*})^{T}\Sigma _{w}x^{*}+\sigma ^{2})$$

三、总结

本文是从贝叶斯的角度解释线性回归，可以发现，在数学的世界中，虽然可能每一派对方法的定义不同，但道路殊途同归，工具是用来解决问题的，各有各的好坏之分。

频率主义方法解决了这个问题，但忽略了一些关键信息;答案的不确定性，但是我们看到贝叶斯方法不仅会给出最可能的答案，还会告诉我们这个答案的不确定程度。

“本文正在参加 人工智能创作者扶持计划”